Определение геометрических параметров передачи и колес

При проектировочном расчете передач с прямозубыми колесами, имеющими твердость Н_HB ≤ 350 НВ, рекомендуется первоначально из условия контактной прочности вычислять внешний делительный диаметр колеса d_{е 2} [14]:

где K_d – вспомогательный коэффициент, учитывающий тип передачи: K_d = 99 – для прямозубых передач, K_d = 86 – для косозубых передач [14];

K_{Н β} – коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца, принимают по графику (рис. 6.3) в зависимости от отношения K_bе × U / (2 – K_bе); K_bе – коэффициент ширины зубчатого венца b относительно внешнего конусного расстояния R_e; рекомендуется K_bе = 0,2–0,3;

– коэффициент ширины зубчатого венца; при проектировании редукторов со стандартными параметрами принимается ψ _bRe = 0,285 (ГОСТ 12.289–76).

Так как K_{Н β} = 1,2 (рис. 6.3):

Полученную величину округляем до номинального значения внешнего делительного диаметра колеса по ГОСТ 12289–76 d_{е 2} = 225 мм. Принимаем рабочую ширину зацепления по ГОСТ 12289–76 b_w = 34 мм. В дальнейших расчетах следует учитывать требования стандарта по выполнению следующих условий: b_w ≤ 0,3 R_e, b_w ≤ 10 m_e.

Согласно рекомендациям [14], число зубьев конической шестерни z ₁ = 18–32. Принимаем z ₁ = 19, тогда z ₂ = u × z ₁ = 3,15 × 19 = 59,85; принимаем z ₂ = 60.

Фактическое передаточное число передачи

u _ф = z ₂ / z ₁ = 60 / 19 = 3,158.

Δ u = (u _ф – u) / u · 100 % = (3,158 – 3,15) / 3,15 · 100 % = 0,25 %,

что допустимо.

Внешний окружной модуль

m_e = d_{e 2} / z ₂ = 225 / 60 = 3,75 мм.

Внешний делительный диаметр шестерни

d_{e 1} = d_{е 2} / u = 225 / 3,158 = 71,25 мм.

Определим углы делительных конусов [14]:

tgδ₂ = u = 3,158; δ₂ = arctg 3,158 = 72,429° = 72°25'45'';

δ₁ = 90 – δ₂; δ₁ = 90° – 72°25'45'' = 17,57°= 17°34'15''.

Внешнее конусное расстояние

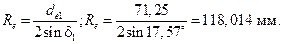
Среднее конусное расстояние

R = R_e – 0,5 × b = 118,014 – 0,5 × 34 = 101,014 мм.

Средний окружной модуль:

m = m _e · R / R_e = 3,75 · 101,014 / 118,014 = 3,21 мм.

Средний делительный диаметр:

d ₁ = d_{е 1} – b · sinδ₁ = m · z ₁ = 3,21 · 19 = 60,99 мм;

d ₂ = m · z ₂ = 3,21 · 60 = 192,6 мм.

Коэффициент смещения

где β _m = 0, так как передача прямозубая;

x ₂ = – x ₁ = –0,412.

Коэффициент расчетной толщины зуба исходного контура

x _τ1 = 0,03 + 0,008 (u – 2,5) = 0,03 + 0,008 (3,158 – 2,5) = 0,035;

x _τ2 = – x _τ1 = –0,035.

Внешняя высота головки зуба

h _{a e 1} = (1 + x ₁) m_e = (1 + 0,412) 3,75 = 5,295 мм;

h _{a e 2} = (1 + x ₂) m_e = (1 – 0,412) 3,75 = 2,205 мм.

Внешняя высота ножки зуба

h _{fe 1} = h _{a e 2} + 0,2 · m_e = 2,205 + 0,2 · 3,75 = 2,955 мм;

h _{fe 2} = h _{a e 1} + 0,2 · m_e = 5,295 + 0,2 · 3,75 = 6,045 мм.

Внешняя высота зуба

h_{e 1} = h _{a e 1} + h _{fe 1} = 5,295 + 2,955 = 8,25 мм;

h_{e 2} = h _{a e 2} + h _{fe 2} = 2,205 + 6,045 = 8,25 мм.

Внешняя окружная толщина зуба

S_{e 1} = (0,5π + 2 x ₁tgα + x _τ1) m_e =

= (0,5π + 2·0,412·tg20° + 0,035) 3,75 = 7,14 мм;

S_{e 2} = π m_e – S_{e 1} = π·3,75 – 7,14 = 4,64 мм.

Угол ножки зуба

θ _{f 1} = arctg(h_{fe 1} / R_e) = arctg(2,955 / 118,014) = 1,4344° = 1°26'4'';

θ _{f 2} = arctg(h_{fe 2} / R_e) = arctg(6,045 / 118,014) = 2,9323°= 2°55'56''.

Угол головки зуба

θ _{a 1} = θ _{f 2} = 2°55'56''; θ _{a 2} = θ _{f 1} = 1°26'4''.

Угол конуса вершин

δ _{а 1} = δ₁ + θ _{a 1} = 17°34'15'' + 2°55'56'' = 20°30'11'';

δ _{а 2} = δ₂ + θ _{a 2} = 72°25'45'' + 1°26'4'' = 73°51'49''.

Угол конуса впадин

δ _{f 1} = δ₁ – θ _{f 1} = 17°34'15'' – 1°26'4'' = 16°8'11'';

δ _{f 2} = δ₂ – θ _{f 2} = 72°25΄45'' – 2°55'56'' = 69°29'49''.

Внешний диаметр вершин зубьев

d_{ae 1} = d_{е 1} + 2 h_{a e 1} · cos δ₁ = 71,25 + 2 · 5,295 · cos 17°34'15'' = 81,346 мм;

d_{ae 2} = d_{е 2} + 2 h _{a e 2} · cos δ₂ = 225 + 2 · 2,205 · cos 72°25'45'' = 226,33 мм.

Проверим коэффициенты ширины венца:

ψ _bRe = b_w / R_e = 34 / 118,014 = 0,288 < 0,3;

ψ _bd = b_w / d ₁ = 34 / 60,99 = 0,557.

Условия выполняются.

Средняя окружная скорость зубчатых колес.

υ = π · d ₁ · n ₁ / 60 = 3,14 · 60,99 · 10^–3 · 949 / 60 = 3,03 м/с.

Принимаем 8-ю степень точности изготовления зубчатых колес (табл. 5.6).

Определяем значения усилий в коническом зацеплении:

– окружная сила на шестерне и колесе:

F_{t 1} = F_{t 2} = 2 · Т ₂ / d_{wm 2} = 2 · 113230 / 192,825 = 1174,43 Н;

d_{wm 2} = 0,857 d_{е 2} = 0,857 · 225 = 192,825 мм;

– радиальная сила на шестерне, численно равная осевой силе на колесе:

F_{r 1} = F_{а 2} = F_t · tg α · cos δ₁ =

= 1174,43 · tg 20° · cos 17°34'15'' = 407,565 Н;

– осевая сила на шестерне, численно равная радиальной силе на колесе:

F_{а 1} = F_{r 2} = F_t · tg α · sin δ₁ =

= 1174,43 · tg 20° · sin 17°34'15'' = 129,053 Н,

где d_wm – средний начальный диаметр;

α – угол профиля исходного контура;

δ – угол делительного конуса.

Изобразим схему действия сил (рис. 6.2).

Рис. 6.2. Схема действия сил в прямозубом коническом зацеплении

Произведем проверку передачи по контактным напряжениям.

Date: 2015-10-21; view: 444; Нарушение авторских прав