Инерционное осаждение частиц

При обтекании твердого тела (или капли) запыленным потоком частицы, вследствие большей инерции, продолжают двигаться поперек изогнутых линий тока газов (рис. 4.3) и осаждаются на поверхности тела. Такое осаждение называется инерционным. Коэффициент эффективности инерционного осаждения η_Stk определяется долей частиц, извлеченных из потока при обтекании им тела. Иногда его называют «эффективность мишени».

Траектория движения частицы в газовом потоке может быть описана уравнениями:

;

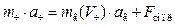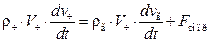, (4.19)

где m _ч – масса частицы;

m _г (V _ч) – масса газа среды, в котором движется частица, заключенного в объеме, равном объему частицы V _ч;

и – ускорения, испытываемые массами m _ч и m _г соответственно;

v _ч, v _г – скорости частицы и газов в месте нахождения частицы соответственно;

t – время движения.

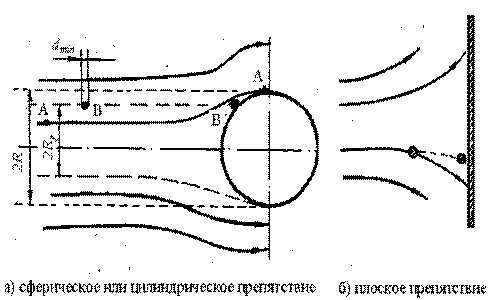
Рис. 4.3

Если газовый поток движется стационарно, а закон движения частицы лежит в области применимости закона Стокса (см. формулу (4.6)), то уравнение (4.19) можно записать в безразмерном виде:

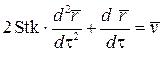, (4.20)

где 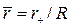– безразмерная координата частицы ( 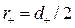– радиус частицы, R – характерный размер обтекаемого тела, например радиус шара или цилиндра, м);

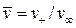– безразмерная скорость частицы, где v _∞ – скорость невозмущенного потока или скорость газов вдали от обтекаемого тела, м/с;

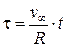– безразмерное время;

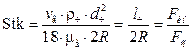– критерий Стокса, или «инерционный параметр», характеризующий отношение инерционной силы, действующей на частицу к силе гидравлического сопротивления среды. Критерий численно равен отношению расстояния 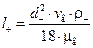, проходимого частицей с начальной скоростью v _г при отсутствии внешних сил до остановки, к характерному размеру обтекаемого тела (например диаметру шара или цилиндра).

Если движение частицы осуществляется в области, где закон Стокса неприменим, т.е. F _с ≠ F _Stk, необходимо ввести поправку, учитывающую отношение истинной силы сопротивления F _с к «стоксовскому» сопротивлению F _Stk, равную , где 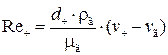– критерий Рейнольдса для частицы. В этом случае закон движения частицы запишется в виде

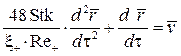. (4.21)

Анализируя уравнения (4.20) и (4.21), можно сделать вывод, что критерий Стокса Stk является единственным критерием подобия инерционного осаждения. Это означает, что эти уравнения применимы к геометрически подобным системам с одинаковым значением числа Рейнольдса Re; в этом случае подобие конфигураций линий тока будет соблюдено вне зависимости от различий между скоростями движения.

Из уравнений (4.20) и (4.21) следует, что при Stk = 0, т.е для частиц с бесконечно малой массой, скорость их движения равна 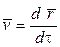, т.е. частица точно следует по линии тока, v _ч = v _г, не соприкасаясь с поверхностью обтекаемого тела. Очевидно, такое же явление будет наблюдаться и при достаточно малых значениях критерия Стокса. Существует определенное минимальное, так называемое критическое значение числа Стокса: Stk_min = Stk_кр, при котором инерция частицы оказывается достаточной, чтобы преодолеть увлечение ее газовым потоком, и она достигает поверхности тела, т.е. осаждение частицы на препятствии возможно лишь при условии

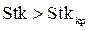. (4.22)

Таким образом, зная критическое значение числа Стокса Stk_кр:

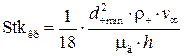, (4.23)

где h – ширина невозмущенного потока (т.е. 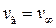) перед препятствием (обычно принимается, что ширина невозмущенного потока равна размеру препятствия, т.е. h ≈ 2 R), можно определить минимальный размер частицы d _{ч min}, осаждаемой на препятствии:

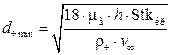. (4.24)

Считается, что при размере частицы d _ч < d _{ч min} она не может быть уловлена при инерционном осаждении, а сама степень очистки под действием инерционных сил является зависимостью вида

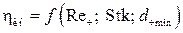. (4.25)

В общем случае инерционное осаждение (сепарация) взвешенных частиц твердых аэрозолей (пыли) происходит под действием множества факторов, основными из которых являются:

– во-первых, силы инерции, перемещающие частицу из основного потока на его периферию;

– во-вторых, более крупные частицы, движущиеся быстрее и увлекающие за собой более мелкие (так называемое явление кинематической коагуляции);

– в-третьих, при инерционном осаждении наблюдается переходная зона между движущимся основным потоком и неподвижными слоями, что вызывает «местные» вихри запыленных частиц, которые способствуют вторичному уносу осажденных частиц с препятствия обратно в поток;

– в-четвертых, возможен вторичный унос, который наблюдается при столкновении и разрушении непрочных пылевидных агрегатов на более мелкие;

– в-пятых, возможно осаждение частиц также при непосредственном набегании основного потока на препятствие (рис. 4.3б) с учетом эффекта зацепления.

Следует также отметить, что теория инерционного осаждения рассматривает осаждение частиц на фронтальной (передней) части обтекаемого тела и не учитывает их осаждение на задней поверхности тела, которое может происходить за счет турбулентных пульсаций газового потока. Это явление становится существенным при малых значениях критерия Stk, т.е. при улавливании субмикронных частиц пыли. Поэтому на практике, даже при Stk < Stk_кр, эффективность осаждения не равна нулю.

Date: 2015-09-24; view: 1650; Нарушение авторских прав