
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кручение
|
|
Этот вид деформации характеризуется взаимным поворотом поперечных сечений стержня под влиянием моментов (пар сил), действующих в плоскости этих сечений. Кручение возникает, например, когда нижнее основание стержня закреплено, а верхнее основание поворачивают вокруг продольной оси (рис. 6.7).
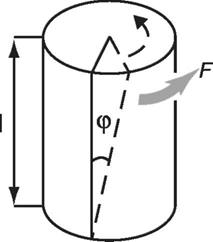 Рис. 6.7. Деформация кручения
Рис. 6.7. Деформация кручения
При этом расстояние между различными слоями остается практически неизменным, но точки слоев, лежащие на одной вертикали, сдвинуты относительно друг друга. Этот сдвиг в разных местах будет различен. Например, в центре сдвига совсем не будет, по краям он будет максимальный.
Таким образом, деформация кручения сводится к неоднородному сдвигу.
Абсолютная деформация при кручении характеризуется углом поворота (φ) одного основания относительно другого.
Относительная деформация (θ) равна отношению угла φ к длине стержня l:
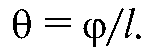 Сопротивление кручению очень быстро возрастает с увеличением радиуса, поэтому органы, рассчитанные на выполнение крутильных движений, как правило, длинные и тонкие (шея птиц, тело змеи).
Сопротивление кручению очень быстро возрастает с увеличением радиуса, поэтому органы, рассчитанные на выполнение крутильных движений, как правило, длинные и тонкие (шея птиц, тело змеи).
Сравнивания различные способы деформирования однородных тел, можно увидеть, что все они сводятся к комбинации растяжения (сжатия) и сдвига.
- Виды деформации
Деформации растяжения и сжатия. Если к однородному, закрепленному с одного конца стержню приложить силу F вдоль его оси в направлении от стержня, то он подвергнется деформации растяжения. Деформацию растяжения испытывают тросы, канаты, цепи в подъемных устройствах, стяжки между вагонами и т. д. Если на закрепленный стержень подействовать силой вдоль его оси по направлению к стержню, то он подвергнется сжатию. Деформацию сжатия испытывают столбы, колонны, стены, фундаменты зданий и т. п. При растяжении или сжатии изменяется площадь поперечного сечения тела.
Деформация сдвига. Деформацию сдвига можно наглядно продемонстрировать на модели твердого тела, представляющего собой ряд параллельных пластин, соединенных между собой пружинами (рис. 3).Горизонтальная сила F сдвигает пластины друг относительно друга без изменения объема тела. У реальных твердых тел при деформации сдвига объем также не изменяется. Деформации сдвига подвержены заклепки и болты, скрепляющие части мостовых ферм, балки в местах опор и др. Сдвиг на большие углы может привести к разрушению тела – срезу. Срез происходит при работе ножниц, долота, зубила, зубьев пилы и т. д.

Рис. 3.
Деформация изгиба. Легко согнуть стальную или деревянную линейку руками или с помощью какой-либо другой силы. Балки и стержни, расположенные горизонтально, под действием силы тяжести или нагрузок прогибаются – подвергаются деформации изгиба. Деформацию изгиба можно свести к деформации неравномерного растяжения и сжатия. Действительно, на выпуклой стороне (рис. 4) материал подвергается растяжению, а на вогнутой – сжатию. Причем чем ближе рассматриваемый слой к среднему слою KN,тем растяжение и сжатие становятся меньше. Слой KN,не испытывающий растяжения или сжатия, называется нейтральным. Так как слои АВ и CD подвержены наибольшей информации растяжения и сжатия, то в них возникают наибольшие силы упругости (на рисунке 4 силы упругости показаны стрелками). От внешнего слоя к нейтральному эти силы уменьшаются. Внутренний слой не испытывает заметных деформаций и не противодействует внешним силам, а поэтому является лишним в конструкции. Его обычно удаляют, заменяя стержни трубами, а бруски – тавровыми балками (рис. 5). Сама природа в процессе эволюции наделила человека и животных трубчатыми костями конечностей и сделала стебли злаков трубчатыми, сочетая экономию материала с прочностью и меткостью «конструкций».
Деформация кручения. Если на стержень, один из концов которого закреплен (рис. 6), подействовать парой сил, лежащей в плоскости поперечного сечения стержня, то он закручивается. Возникает, как говорят, деформация кручения.
Каждое поперечное сечение поворачивается относительно другого вокруг оси стержня на некоторый угол. Расстояние между сечениями не меняется. Таким образом, опыт показывает, что при кручении стержень можно представить как систему жестких кружков, насаженных центрами на общую ось.Кружки эти (точнее, сечения) поворачиваются на различные углы в зависимости от их расстояния до закрепленного конца. Слои поворачиваются, но на различные углы. Однако при этом соседние слои поворачиваются друг относительно друга одинаково вдоль всего стержня. Деформацию кручения можно рассматривать как неоднородный сдвиг. Неоднородность сдвига выражается в том, что деформация сдвига изменяется вдоль радиуса стержня. На оси деформация отсутствует, а на периферии она максимальна. На самом удаленном от закрепленного конца торце стержня угол поворота наибольший. Его называют углом кручения. Кручение испытывают валы всех машин, винты, отвертки и т. п.
Основными деформациями являются деформации растяжения (сжатия) и сдвига. При деформации изгиба происходит неоднородное растяжение и сжатие, а при деформации кручения – неоднородный сдвиг.
| Вид деформации | Признаки |
| Растяжения | увеличивается расстояние между молекулярными слоями. |
| Сжатия | уменьшается расстояние между молекулярными слоями. |
| Кручения | поворот одних молекулярных слоев относительно других. |
| Изгиба | одни молекулярные слои растягиваются, а другие сжимаются или растягиваются, но меньше первых. |
| Сдвига | одни слои молекул сдвигаются относительно других. |
| Упругая | после прекращения воздействия тело полностью восстанавливает первоначальную форму и размеры. |
| Пластичная | после прекращения воздействия тело не восстанавливает первоначальную форму или размеры. |
- Механические модели деформации биологических сред (модель Максвелла)
Вязкоупругие свойства тел (сочетание вязкого течения и высокой эластичности) моделируются системами, состоящими из различных комбинаций двух простых элементов: 1) пружины (упругий элемент) и 2) поршня с отверстиями, движущегося в цилиндре с вязкой жидкостью (вязкий элемент). Эти элементы и «конструируемые» с их помощью модели показаны на рис. 6.19 слева. Справа показаны зависимости деформации (ε) от времени при импульсном воздействии внешней силы: в момент времени t = 0 к телу, поведение которого моделируется, прикладывается постоянная сила F; в момент времени t1 действие силы прекращается.
Моделью упругого тела является пружина (рис. 6.19, а), подчиняющаяся закону Гука. Деформация (ε) мгновенно появляется в момент t = 0 и мгновенно исчезает в момент t1.
Моделью вязкого тела является поршень с отверстиями, движущийся в цилиндре с вязкой жидкостью (рис. 6.19, б). Связь между скоростью деформации вязкой среды (скоростью перемещения поршня) и напряжением имеет вид
 Модель Максвелла
Модель Максвелла
В модели Максвелла упругий и вязкий элементы соединены последовательно (рис. 6.19, в). Напряжение в каждом элементе является 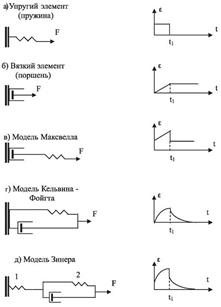 Рис. 6.19. Механические модели вязкоупругих тел и динамика развития деформации
Рис. 6.19. Механические модели вязкоупругих тел и динамика развития деформации
одинаковым. В любой момент времени для деформации выполняется условие
 Решение этого уравнения приводит к следующему характеру развития деформации. В момент t = 0 пружина мгновенно растягивается, а затем начинается линейное нарастание деформации, связанное с движением поршня. В момент t1 пружина сокращается до начального размера, а поршень останавливается - имеет место остаточная деформация.
Решение этого уравнения приводит к следующему характеру развития деформации. В момент t = 0 пружина мгновенно растягивается, а затем начинается линейное нарастание деформации, связанное с движением поршня. В момент t1 пружина сокращается до начального размера, а поршень останавливается - имеет место остаточная деформация.
С помощью модели Максвелла можно моделировать следующие механические процессы.
Релаксация напряжения в материале: ε = const, dε/dt = 0, т.е. поддерживается постоянная деформация. В этом случае из уравнения (6.10) следует
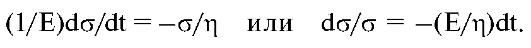 Интегрируя последнее выражение от начального момента времени и начального напряжения σ о до текущих значений t иσ, получаем выражение, описывающее изменение напряжения со временем, т.е. релаксацию напряжения:
Интегрируя последнее выражение от начального момента времени и начального напряжения σ о до текущих значений t иσ, получаем выражение, описывающее изменение напряжения со временем, т.е. релаксацию напряжения:
 т.е. под действием постоянной приложенной силы происходит вязкое течение (поршень движется с постоянной скоростью).
т.е. под действием постоянной приложенной силы происходит вязкое течение (поршень движется с постоянной скоростью).
При изучении свойств волос используют явление релаксации напряжения в них. Этот процесс аппроксимируют моделью, состоящей из 4 параллельно соединенных моделей Максвелла.
Date: 2015-09-24; view: 2090; Нарушение авторских прав