Растяжение (сжатие)

Этот вид деформации возникает, когда к стержню (бруску) с закрепленным основанием прикладывается сила F, направленная вдоль его оси (рис. 6.1, а). Под действием этой силы длина стержня увеличивается на некоторую величину Δ l (l - первоначальная длина).

При этом в каждом сечении стержня возникают направленные по нормали силы (F₁ и F₂), равные по величине приложенной силе F и обусловленные изменением расстояния между частицами при растяжении. Сила F₁ действует на верхнюю часть бруска со стороны нижней части; сила F₂ - наоборот (рис. 6.1, б).

Состояние растянутого тела характеризуется продольным (нормальным) напряжением σ, которое может быть вычислено для любого сечения тела, перпендикулярного приложенной силе.

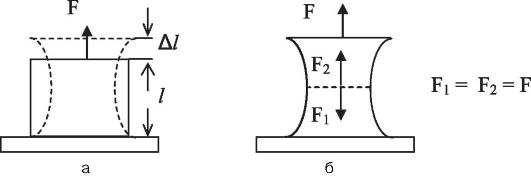Рис. 6.1. Деформация растяжения (а); силы, возникающие при растяжении (б)

Нормальное напряжение равно отношению модуля силы, возникающей в данном сечении в результате растяжения, к площади сечения:

В СИ механическое напряжение измеряется в паскалях (Па).

Величина абсолютной деформации А! зависит от первоначальной длины стержня, поэтому степень деформации выражают через отношение абсолютной деформации к первоначальной длине. Это отношение называется относительной деформацией (ε):

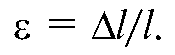Относительная деформация - величина безразмерная. Иногда ее выражают в процентах: ε = (Δ l / l)х100%.

В большинстве случаев при растяжении или сжатии степень деформации в различных сечениях стержня различна. Это можно увидеть, если на поверхность тела нанести квадратную сетку. После деформирования сетка исказится. По характеру и величине этого искажения можно судить о распределении напряжения вдоль образца (рис. 6.2).

Видно, что изменения формы ячеек сетки максимальны в средней части стержня и почти отсутствуют на его краях.

Опытным путем было установлено, что небольшие деформации исчезают после снятия внешнего воздействия. Такие деформации называются упругими. Для них выполняется закон Гука:

При упругой деформации напряжение прямо пропорционально величине относительной деформации:

Коэффициент пропорциональности Е характеризует упругие свойства вещества при растяжении (сжатии) и называется модулем Юнга (модуль продольной упругости, Па). В таблице 6.1 представлены значения модулей упругости некоторых материалов.

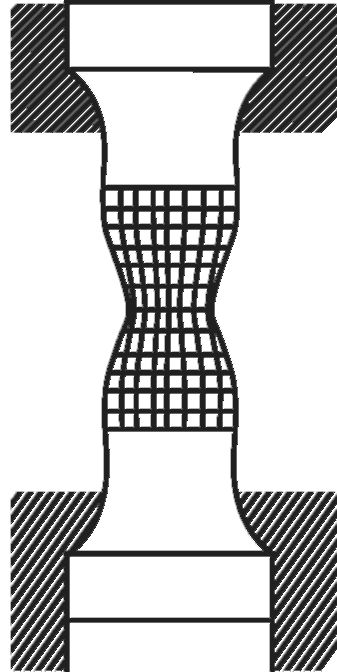Рис. 6.2. Искажение квадратной сетки при растяжении стержня

Сдвиг

Деформация сдвига возникает, если на тело действует касательная сила, приложенная параллельно закрепленному основанию (рис. 6.3, а).

В этом случае направление смещения свободного основания параллельно приложенной силе и перпендикулярно боковой грани. В результате деформации сдвига

прямоугольный параллелепипед превращается в косоугольный. При этом боковые грани смещаются на некоторый угол γ, называемый углом сдвига.

При сдвиге в каждом сечении стержня возникают касательные силы (F₁ и F₂), равные по величине приложенной силе F и обусловленные изменением расстояния между частицами (рис. 6.3, б). Сила F₁действует на верхнюю часть бруска со стороны нижней части; сила F₂ - наоборот.

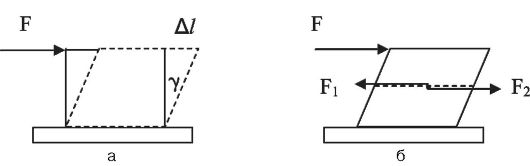Рис. 6.3. Деформация сдвига (а); силы, возникающие при сдвиге (б)

Состояние тела при наличии деформации сдвига характеризуется касательным напряжением τ, которое может быть вычислено для любого сечения тела, параллельного закрепленному концу.

Касательное напряжение равно отношению модуля силы, возникающей в данном сечении в результате сдвига, к площади сечения:

Абсолютная деформация сдвига измеряется величиной смещения свободного основания Δ l. Относительная деформация сдвига определяется через тангенс угла сдвига tgγ, называемый относительным сдвигом. Так как угол γ обычно мал, то можно считать tg(γ) ≈ γ.

При небольшой величине относительной деформации сдвига связь между деформацией и механическим напряжением выражается законом Гука:

Коэффициент пропорциональности G характеризует упругие свойства вещества при сдвиге и называется модулем сдвига (Па).

Date: 2015-09-24; view: 539; Нарушение авторских прав