
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Уравнение неразрывностиструи
|
|
При ламинарном (слоистом) течении жидкости произведение площади сечения трубки тока на скорость жидкости в этом сечении является величиной постоянной вдоль линии тока
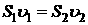 , (72)
, (72)
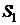 и
и 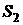 - площади сечений 1 и 2 трубки тока,
- площади сечений 1 и 2 трубки тока, 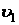 и
и 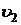 - скорости частиц жидкости в этих сечениях.
- скорости частиц жидкости в этих сечениях.
В гидродинамике жидкости делятся на ньютоновские и неньютоновские. Течение ньютоновской жидкости подчиняется закону вязкости Ньютона, то есть касательное напряжение и градиент скорости линейно зависимы. Коэффициент пропорциональности между этими величинами известен как вязкость[3][4][5]. У неньютоновской жидкости вязкость зависит от градиента скорости
- Уравнение Бернулли и его практическое применение.
Закон (уравнение) Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
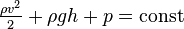
Здесь
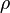 — плотность жидкости,
— плотность жидкости,
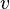 — скорость потока,
— скорость потока,
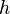 — высота, на которой находится рассматриваемый элемент жидкости,
— высота, на которой находится рассматриваемый элемент жидкости,
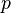 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
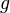 — ускорение свободного падения.
— ускорение свободного падения.
В научной литературе закон Бернулли, как правило, называется уравнением Бернулли [1](не следует путать сдифференциальным уравнением Бернулли), теоремой Бернулли [2][3] или интегралом Бернулли [4][5].
Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.
Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»[6]).
Соотношение, близкое[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.
Для горизонтальной трубы 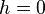 и уравнение Бернулли принимает вид:
и уравнение Бернулли принимает вид: 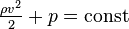 .
.
Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности 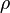 :
: 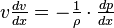 .
.
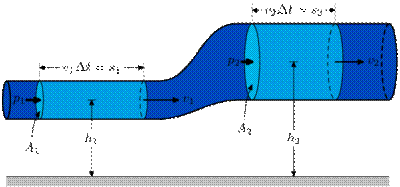

Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.
Полное давление состоит из весового 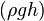 , статического
, статического 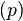 и динамического
и динамического 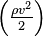 давлений.
давлений.
Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины —гидравлики.
Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.
Для потока реальной вязкой жидкости следует учитывать различие в скоростях по сечению потока. В практических расчетах пользуются понятием средней скорости. При этом расчетное значение удельной кинетической энергии потока получается несколько меньше действительного. Последнее обстоятельство учитывается введением поправочного коэффициента α, определенного опытным путем.
Для ламинарного режима движения жидкости в круглых трубах α=2, для турбулентного α=1,04÷1,13.
В реальных условиях необходимо учитывать также потери напора на участке от первого до второго исследуемых сечений потока – hпот.
Потеря напора (м) на участке складывается из потерь на трение (линейные потери) hл и потерь на местные сопротивления hм
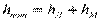 .
.
С учетом сказанного уравнение Бернулли для потока реальной жидкости записывают в следующем виде:
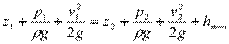 .
.
При использовании обозначений пьезометрического hp и скоростного h v напоров уравнение Бeрнулли можно записать и так:
z1 + hp1 + h v 1 = z2 + hp2 + h v 2 + D H.
Энергетический смыслуравнения Бeрнулли заключается в том, что оно отражает закон сохранения энергии: сумма потенциальной z+hp, кинетической v 2 / 2g энергии и энергии потерь ∆ H остаётся неизменной во всех точках потока.
Геометрический смысл уравнения Бeрнулли показан на рис. 10: сумма четырёх высот z, hp, h v, ∆ H остаётся неизменной во всех точках потока.
Определение расхода жидкости. В длинных трубопроводах и каналах произвольных сечений измерение расхода без нарушения целостности потока может быть выполнено с помощью водомера Вентури.
Для определения расхода жидкости измеряют пьезометрические напоры в цилиндрических участках водомера Вентури и определяют их разность ∆h. Если принять hпот=0, α 1= α2=1, то из уравнения Бернулли получим:
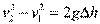 .
.
Решая полученное уравнение совместно с уравнением неразрывности потока, получим выражение для скорости в первом сечении
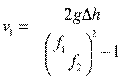 ,
,
где f1 и f2 – площади соответственно первого и второго сечений.
Расход жидкости (м3/сек), протекающей через прибор, определится как произведение скорости v1 на площадь поперечного сечения f1:
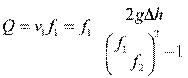 ,.
,.
С учетом коэффициента расхода μ формула принимает вид:

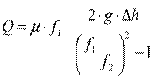 .
.
Как правило, μ=0,96÷0,98.
Идеальная жидкость — жидкость, плотность которой не зависит от давления, а при ее движении отсутствуют силы внутреннего трения.
Линия тока — линия, в каждой точке которой касательная к ней указывает направление вектора скорости. Чем больше скорость течения жидкости, тем больше густота линий тока.
Трубка тока — часть жидкости, ограниченная линиями тока. Через каждое сечение трубки тока за 1 секунду проходит один и тот же объем:  — уравнение неразрывности.
— уравнение неразрывности.
Уравнение Бернулли
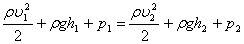 , где
, где 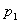 и
и 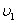 — давление и скорость жидкости на высоте
— давление и скорость жидкости на высоте 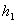 ,
, 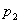 и
и 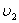 — давление и скорость жидкости на высоте
— давление и скорость жидкости на высоте 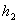 .
.
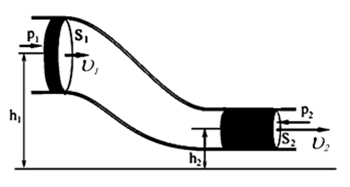
Формула Торричелли. Скорость жидкости, вытекающей из отверстия на глубине  от поверхности, равна скорости, которую приобретает тело, падая с высоты
от поверхности, равна скорости, которую приобретает тело, падая с высоты  :
:
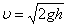 . Формула Торричелли — следствие из уравнения Бернулли.
. Формула Торричелли — следствие из уравнения Бернулли.
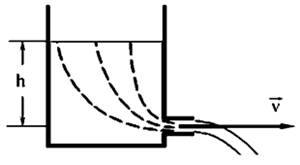
- Ламинарное и турбулентное течение жидкости. Число Рейнольдса
Ламинарное течение – упорядоченный режим течения вязкой жидкости, характеризующийся отсутствием перемешивания между слоями жидкости.
Течение жидкости с завихрениями называется турбулентным.
При малых скоростях течения случайно возникающие в потоке завихрения гаснут, не вызывая заметного перемешивания слоев. При высоких скоростях течения жидкости создаются условия, при которых течение перестает быть устойчивым и под влиянием случайных возмущений переходит в турбулентное.
Наличие условий, при которых ламинарное течение перестает быть устойчивым, зависит от числа Рейнольдса:
 (25)
(25)
где v – скорость течения жидкости, S – сечение трубы, r - плотность жидкости, h - вязкость жидкости.
Как правило, значение критического числа Рейнольдса определяют экспериментально. Для гладких труб Reкр = 2300.
Если Reкр известно, то становится возможным для любой жидкости и разных условий ее течения предсказать, будет ли ее поток ламинарным или турбулентным. Если для определенного течения число Рейнольдса не превышает некоторого критического значения Reкр, ламинарное течение устойчиво. Если же Re > Reкр, то в потоке жидкости возникают завихрения - ее течение становится турбулентным.
Reкр 1600. Движение крови в организме, в основном, ламинарное. Однако, при определенных условиях, кровоток может приобретать и турбулентный характер.¸для крови равно 900
Турбулентность проявляется в полостях сердца (велико значение d), в аорте и вблизи клапанов сердца (высокая скорость движения крови). При интенсивной физической нагрузке скорость движения крови увеличивается, и это может вызвать турбулентность в кровотоке.
С уменьшением вязкости турбулентный характер течения жидкости может проявляться и при сравнительно небольшой скорости ее движения (см. формулу 25). Поэтому, при некоторых патологических процессах, приводящих к аномальному снижению вязкости крови, кровоток в крупных кровеносных сосудах может стать турбулентным.
Кровеносный сосуд не всегда можно моделировать гладкой трубой. В частности, при наличии атеросклеротических бляшек в просвете сосудов имеются локальные сужения, приводящие к возникновению турбулентности в течении крови. Турбулентность в кровотоке сопровождается шумами, прослушиваемыми с помощью фонендоскопа.
- Идеальная жидкость. Законы Пуазейля и Стокса
Идеа́льная жи́дкость — в гидродинамике — воображаемая несжимаемая жидкость, в которой отсутствуют вязкость и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.
Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемыхгидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.
Закон Пуазейля представляет собой формулу для объемной скорости течения жидкости. Он был открыт экспериментально французским физиологом Пуазейлем, который исследовал течение крови в кровеносных сосудах. Закон Пуазейля часто называют главным законом гидродинамики.
Закон Пуазейля связывает объемную скорость течения жидкости с разностью давления в начале и конце трубки как движущей силой потока, вязкостью жидкости, радиусом и длиной трубки. Закон Пуазейля используют в случае, если течение жидкости ламинарное. Формула закона Пуазейля:
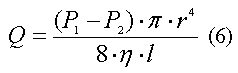
|
где Q - объемная скорость жидкости (м3/с), (P1- P2) - различие давления через концы трубки (Па), r - внутренний радиус трубки (м), l - длина трубки (м), η - вязкость жидкости (Па с).
Закон Пуазейля показывает, что величина Q пропорциональна разнице давления P1- P2 в начале и конце трубки. Если P1 равняется P2, поток жидкости прекращается. Формула закона Пуазейля также показывает, что высокая вязкость жидкости приводит к снижению объемной скорости течения жидкости. Оно также показывает, что объемная скорость жидкости чрезвычайно зависима от радиуса трубки. Это подразумевает, что умеренные изменения радиуса кровеносных сосудов могут обеспечивать большие различия объемной скорости жидкости, протекающей через сосуд.
Формула закона Пуазейля упрощается и становится более универсальной при введении вспомогательной величины - гидродинамического сопротивления R, которое для цилиндрической трубки может быть определено по формуле:
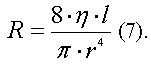
|
Закон Пуазейля, таким образом, показывает, что объемная скорость жидкости прямо пропорциональна разнице давления в начале и конце трубки и обратно пропорциональна гидродинамическому сопротивлению:
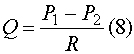
|
Течение Пуазейля - ламинарное течение жидкости через тонкие цилиндрические трубки. Описывается законом Пуазейля.
Окончательно потери напора при ламинарном движении жидкости в трубе: 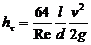
Несколько преобразовав формулу для определения потерь напора, получим формулу Пуазейля: 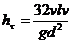
Закон установившегося течения в вязкой несжимаемой жидкости в тонкой цилиндрической трубке круглого сечения. Сформулирован впервые Готтфильхом Хагеном в 1839 и вскоре повторно выведен Ж.Л. Пуазейлем в 1840. Согласно закону, секундный объемный расход жидкости пропорционален перепаду давления на единицу длины трубки. Закон Пуазейля применим только при ламинарном течении и при условии, что длина трубки превышает так называемую длину начального участка необходимую для развития ламинарного течения в трубке.
Свойства течения Пуазейля:
-Течение Пуазейля характеризуется параболическим распределением скорости по радиусу трубки.
-В каждом поперечном сечении трубки средняя скорость вдвое меньше максимальной скорости в этом сечении.
Из формулы Пуазейля видно, что потери напора при ламинарном движении пропорциональны первой степени скорости или расхода жидкости.
Формулой Пуазейля пользуются при расчетах показателей транспортировки жидкостей и газов в трубопроводах различного назначения. Ламинарный режим работы нефте- и газопроводов является наиболее выгодным в энергетическом отношении. Так, в частности, коэффициент трения при ламинарном режиме практически не зависит от шероховатости внутренней поверхности трубы (гладкие трубы).
Гидравлическое сопротивление
в трубопроводах (a. hydraulic resistance; н. hydraulischer Widerstand; ф. resistance hydraulique; и. perdida de presion por rozamiento) - сопротивление движению жидкостей (и газов), оказываемое трубопроводом. Г. с. на участке трубопровода оценивается величиной "потерянного" давления ∆p, представляющего собой ту часть удельной энергии потока, к-рая необратимо расходуется на работу сил сопротивления. При установившемся течении жидкости (газа) в трубопроводе круглого сечения ∆p (н/м2) определяется по формуле
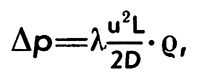
где λ - коэфф. гидравлич. сопротивления трубопровода; u - ср. по сечению скорость потока, м/с; D - внутр. диаметр трубопровода, м; L - длина трубопровода, м; ρ - плотностьжидкости, кг/м3.
Местные Г. с. оцениваются по формуле
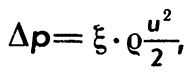
где ξ - коэфф. местного сопротивления.
В процессе эксплуатации магистральных трубопроводов Г. с. возрастает вследствиеотложения парафина (нефтепроводы), скоплений воды, конденсата или образования гидратов углеводородных газов (газопроводы). Для снижения Г. с. производят периодич. очистку внутр. полости трубопроводов спец. скребками или разделителями
В 1851 Джордж Стокс получил выражение для силы трения (также называемой силойлобового сопротивления), действующей на сферические объекты с очень маленькимичислами Рейнольдса (например, очень маленькие частицы) в непрерывной вязкойжидкости, решая уравнение Навье — Стокса:
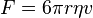
где
· 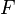 — сила трения, так же называемая силой Стокса,
— сила трения, так же называемая силой Стокса,
·  — радиус сферического объекта,
— радиус сферического объекта,
· 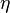 — динамическая вязкость жидкости,
— динамическая вязкость жидкости,
· 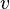 — скорость частицы.
— скорость частицы.
Если частицы падают в вязкой жидкости под действием собственного веса, то установившаяся скорость достигается, когда эта сила трения совместно с силой Архимеда точно уравновешиваются силой гравитации. Результирующая скорость равна
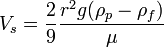
где
· Vs — установившаяся скорость частицы (м/с) (частица движется вниз если 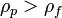 , и вверх в случае
, и вверх в случае 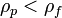 ),
),
·  — радиус Стокса частицы (м),
— радиус Стокса частицы (м),
· g — ускорение свободного падения (м/с²),
· ρp — плотность частиц (кг/м³),
· ρf — плотность жидкости (кг/м³),
· 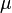 — динамическая вязкость жидкости (Па с).
— динамическая вязкость жидкости (Па с).
- Поверхностное натяжение жидкостей. Капиллярные явления в природе
Каждая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости. В результате появляется равнодействующая сила, направленная вглубь жидкости. Если молекула переместиться с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу.
Силы, действующие на молекулу внутри жидкости со стороны других молекул, взаимно скомпенсированы. Но чтобы вытащить молекулу из глубины жидкости на поверхность надо затратить положительную работу, так как близи поверхности силы межмолекулярного взаимодействия уже не скомпенсированы.
Молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия поверхности жидкости пропорциональна ее площади: 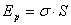 , где
, где 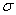 — коэффициент поверхностного натяжения. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = Дж/м2).
— коэффициент поверхностного натяжения. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = Дж/м2).
Коэффициент поверхностного натяжения 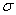 равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу:
равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу: 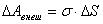 . Коэффициент поверхностного натяжения
. Коэффициент поверхностного натяжения 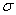 может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
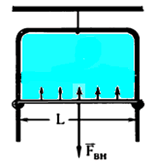
| Силы поверхностного натяжения стремятся сократить поверхность пленки. Для равновесия подвижной стороны рамки к ней нужно приложить внешнюю силу, которая уравновесит силы поверхностного натяжения по обе стороны рамки: 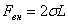 . .
|
В каплях жидкости и внутри мыльных пузырей из-за сил поверхностного натяжения возникает избыточное давление. Если мысленно разрезать сферическую каплю радиуса 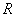 на две половинки, то каждая из них должна находиться в равновесии под действием сил поверхностного натяжения, приложенных к границе
на две половинки, то каждая из них должна находиться в равновесии под действием сил поверхностного натяжения, приложенных к границе 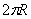 разреза, и сил избыточного давления, действующих на площадь
разреза, и сил избыточного давления, действующих на площадь  сечения.
сечения.
Условие равновесия для капли жидкости: 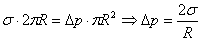 .
.
Условие равновесия для мыльного пузыря: 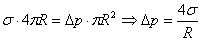
Избыточное давление внутри мыльного пузыря в два раза больше, так как пленка имеет две поверхности.

| Вблизи границы между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела (взаимодействием с молекулами газа можно пренебречь). Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом 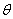 , характерным для данной пары жидкость – твердое тело. Угол , характерным для данной пары жидкость – твердое тело. Угол 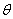 называется краевым углом (рис. 1). Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол называется краевым углом (рис. 1). Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол 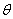 оказывается тупым. В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачивании оказывается тупым. В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачивании 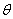 = 0, при полном несмачивании = 0, при полном несмачивании 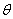 = 180° (рис. 2). = 180° (рис. 2).
|
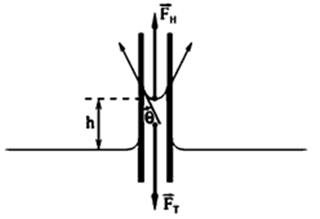
| Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. На рисунке изображена капиллярная трубка некоторого радиуса r, опущенная нижним концом в смачивающую жидкость плотности 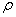 . Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести . Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести 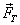 действующая на столб жидкости в капилляре, не станет равной по модулю результирующей действующая на столб жидкости в капилляре, не станет равной по модулю результирующей 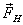 сил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: сил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: 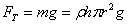 , , 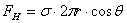 , ,  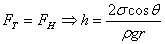
|
При полном несмачивании 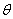 =180°, cos
=180°, cos 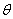 = -1 и, следовательно, h<0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
= -1 и, следовательно, h<0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Вода практически полностью смачивает чистую поверхность стекла. Наоборот, ртуть полностью не смачивает стеклянную поверхность. Поэтому уровень ртути в стеклянном капилляре опускается ниже уровня в сосуде.
Явления смачивания и несмачивания отчетливо проявляются в узких трубках.
Под капиллярными явлениями понимают подъем иди опускание жидкости в узких трубках — капиллярах* — по сравнению с уровнем жидкости в широких трубках.
* От латинского слова capillaris — волосной.
Смачивающая жидкость (например, вода в стеклянной трубке) поднимается по капилляру. При этом, чем меньше радиус трубки, тем на большую высоту поднимается в ней жидкость (рис. 7.25). Жидкость, не смачивающая стенки капилляра (например, ртуть в стеклянной трубке), опускается ниже уровня жидкости в широком сосуде (рис. 7.26).
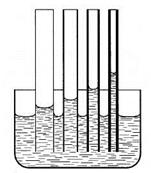
Рис. 7.25
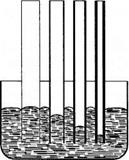
Рис. 7.26
Почему смачивающая жидкость поднимается по капилляру, а несмачивающая опускается? В § 7.5 мы установили, что в случае полного смачивания и полного несмачивания мениск жидкости в узких трубках представляет собой полусферу, радиус которой равен радиусу канала трубки. Под вогнутым мениском смачивающей жидкости давление меньше, чем под плоской поверхностью (см. § 7.6). Поэтому жидкость в узкой трубке (капилляре) поднимается до тех пор, пока гидростатическое давление поднятой в капилляре жидкости на уровне плоской поверхности не скомпенсирует разность давлений. Под выпуклым мениском несмачивающей жидкости давление больше, чем под плоской поверхностью, и это ведет к опусканию несмачивающей жидкости в узких трубках.
Подъем смачивающей жидкости по капилляру можно объяснить по-другому — непосредственным действием сил поверхностного натяжения. Вдоль границы поверхностного слоя жидкости, имеющей форму окружности, на стенки трубки действует сила поверхностного натяжения, направленная вниз (для смачивающей жидкости). Такая же по модулю сила действует на жидкость со стороны стенок трубки вверх (третий закон Ньютона). Эта сила и заставляет жидкость подниматься в узкой трубке. Подъем смачивающей жидкости по капилляру прекратится тогда, когда сила, заставляющая жидкость подниматься вверх, уравновесится силой тяжести, действующей на поднятую жидкость.
^ Высота поднятия жидкости в капиллярных трубках
Пусть жидкость полностью смачивает стенки капилляра. Мениск ее в этом случае имеет форму полусферы (рис. 7.27) радиусом, равным радиусу канала капилляра r. Тогда непосредственно под вогнутым мениском (в точке А) давление жидкости будет меньше атмосферного давления р0 на величину — (см. § 7.6):
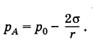 (7.7.1)
(7.7.1)
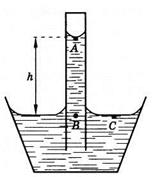
Рис. 7.27
На глубине h, соответствующей уровню жидкости в широком сосуде (в точке В), к этому давлению прибавляется гидростатическое давление ρgh, где ρ — плотность жидкости. В широком сосуде на том же уровне, т. е. непосредственно под плоской поверхностью жидкости (в точке С), давление равно атмосферному давлению р0. Так как жидкость находится в равновесии, то давления на одном и том же уровне (в точках В и С) равны. Следовательно,
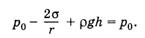 (7.7.2)
(7.7.2)
Отсюда
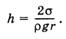 (7.7.3)
(7.7.3)
Высота поднятия жидкости в капилляре прямо пропорциональна поверхностному натяжению ее и обратно пропорциональна радиусу канала капилляра и плотности жидкости.
Глубина h, на которую опускается в капилляре несмачивающая жидкость, тоже вычисляется по формуле (7.7.3). Это утверждение вы можете проверить самостоятельно.
Формулой (7.7.3) можно воспользоваться для определения поверхностного натяжения а. Для этого необходимо по возможности точнее измерить высоту поднятия жидкости h и радиус канала трубки r. Зная плотность жидкости ρ, поверхностное натяжение а можно найти по формуле:
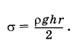
Это один из наиболее распространенных способов определения поверхностного натяжения.
^ Капиллярные явления в природе, быту и технике
Чрезвычайно важно для растений движение и сохранение воды в почве. Почва имеет рыхлое строение, и между отдельными частицами ее находятся промежутки. Узкие промежутки представляют собой капилляры. По капиллярным ходам вода поднимается к корневой системе растений и снабжает их необходимой влагой и питательными солями.
По капиллярам находящаяся в почве вода поднимается вверх и интенсивно испаряется (рис. 7.28). Чтобы уменьшить испарение, нужно разрушить капилляры. Это достигается разрыхлением почвы.
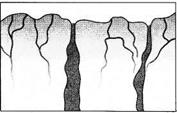
Рис. 7.28
Иногда требуется, наоборот, усилить приток влаги по капиллярам. Тогда почву укатывают, увеличивая этим количество капиллярных каналов.
Любопытно, а может ли вода с растворенными в ней веществами подниматься к верхушкам высоких деревьев за счет поверхностного натяжения (высота, например, секвойи более 100 м). Радиус капилляров в древесине от 0,01 до 0,3 мм. Значит, в самых тонких капиллярах вода не поднимается выше 1,5 м. За счет атмосферного давления она может подняться не выше 10 м, даже если на конце трубки создать вакуум. Не может высоко поднять воду и осмотическое давление, благодаря которому давление в растворе больше, чем в чистой жидкости.
Остается единственное предположение: вода в капиллярах находится в растянутом состоянии, но не разрывается из-за притяжения ее молекул. По мере испарения воды с листьев сила притяжения поднимает ее вверх. Прямые измерения показали, что давление в капиллярах древесины действительно отрицательно и может достигать -25 атм.
В быту капиллярные явления используют при самых разнообразных обстоятельствах. Прикладывая промокательную бумагу, удаляют излишек чернил с письма, хлопчатобумажной или льняной тряпкой вытирают мокрые места на столе или на полу. Применение полотенец, салфеток возможно только благодаря наличию в них капилляров. Поднятие керосина или расплавленного стеарина по фитилям ламп и свечей обусловлено наличием в фитилях капиллярных каналов. В технике как один из способов подвода смазки к деталям машин применяют иногда фитильный способ подачи масла.
В строительном деле приходится учитывать подъем влаги из почвы по порам строительных материалов. Из-за этого отсыревают стены зданий. Для защиты фундамента и стен от воздействия грунтовых вод и сырости применяют гидроизоляцию, покрывая фундамент горячим (жидким) битумом или обкладывая водонепроницаемым рулонным материалом (толь или рубероид).
Узких трубок (капилляров) в природе и технике великое множество. В этих трубках жидкость либо поднимается вверх на высоту 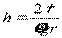 , либо опускается вниз на расстояние, определяемое по той же формуле. Многие процессы в природе и технике вызываются этими движениями.
, либо опускается вниз на расстояние, определяемое по той же формуле. Многие процессы в природе и технике вызываются этими движениями.
- Механические свойства биологических тканей
Механические свойства биологических тканей
Рассмотрим важнейшие механические свойства биологических тканей, благодаря которым осуществляются разнообразные механические явления
– такие, как функционирование опорно-двигательного аппарата, процессы деформаций тканей и клеток, распространение волн упругой деформации, сокращения и расслабление мышц, движение жидких и газообразных биологических сред. Среди этих свойств выделяют:
– упругость – способность тел возобновлять размеры (форму или объем) после снятие нагрузок;
– жесткость – способность материала противодействовать внешней нагрузкой; эластичность – способность материала изменять размеры под действием внешних нагрузок;
– прочность – способность тел противодействовать разрушению под действием внешних сил;
– пластичность – способность тел хранить (полностью или частично) изменение размеров после снятия нагрузок;
– хрупкость – способность материала разрушаться без образования заметных остаточных деформаций;
– вязкость – динамическое свойство, которое характеризует способность тела противодействовать изменению его формы при действии тангенциальных напряжений;
– текучесть – динамическое свойство среды, которое характеризует
способность отдельных его слоев перемещаться с некоторой скоростью в пространстве относительно других слоев этой среды.
Механические свойства мышц
Основная функция мышц состоит в преобразовании химической энергии в механическую работу или силу. Главными биомеханическими показателями, характеризующими деятельность мышцы, являются: а) сила, регистрируемая на ее конце (эту силу называют натяжением или силой тяги мышцы) и б) скорость изменения длины.
При возбуждении мышцы изменяется ее механическое состояние; эти изменения называют сокращением. Оно проявляется в изменении натяжения и длины мышцы, а также других ее механических свойств (упругости, твердости и др.).
Механические свойства мышц сложны и зависят от механических свойств элементов, образующих мышцу (мышечные волокна, соединительные образования и т.п.), и состояния мышцы (возбуждения, утомления и пр.).
Понять многие из механических свойств мышцы помогает упрощенная модель ее строения – в виде комбинации упругих и сократительных компонентов. Упругие компоненты по механическим свойствам аналогичны пружинам: чтобы их растянуть, нужно приложить силу. Работа силы равна энергии упругой деформации, которая может в следующей фазе движения перейти в механическую работу. Различают: а) параллельные упругие компоненты (ПарК) – соединительнотканные образования, составляющие оболочку мышечных волокон и их пучков, и б) последовательные упругие компоненты (ПосК) – сухожилия мышцы, места перехода миофибрилл в соединительную ткань, а также отдельные участки саркомеров, точная локализация которых в настоящее время неизвестна.
Сократительные (контрактильные) компоненты соответствуют тем участкам саркомеров мышцы, где актиновые и миозиновые миофиламенты перекрывают друг друга. В этих участках при возбуждении мышцы происходит механическое взаимодействие между актиновыми и миозиновыми филаментами, приводящее к изменению натяжения и длины мышцы.
Поскольку каждая миофибрилла состоит из большого числа (n) последовательно расположенных саркомеров, то величина и скорость изменения длины миофибриллы в п раз больше, чем у одного саркомера. Сила, развиваемая каждым из них, одинакова и равна силе, регистрируемой на конце миофибриллы (подобно тому, как равны силы в каждом из звеньев цепи, к концам которой приложены растягивающие силы). Эти же самые n саркомеров, соединенные параллельно (что соответствует большему числу миофибрилл), дали бы кратное увеличение в силе, но при этом скорость изменения длины мышцы была бы той же, что и скорость одного саркомера. Поэтому при прочих равных условиях увеличение физиологического поперечника мышцы привело бы к увеличению ее силы, но не изменило бы скорости укорочения, и наоборот, увеличение длины мышцы сказалось бы положительно на скорости сокращения, но не повлияло бы на ее силу.
Покоящаяся мышца обладает упругими свойствами: если к ее концу приложена внешняя сила, мышца растягивается (ее длина увеличивается), а после снятия внешней нагрузки восстанавливает свою исходную длину. Зависимость между величиной нагрузки и удлинением мышцы непропорциональна (не подчиняется закону Гука)
Сначала мышца растягивается легко, а затем даже для небольшого удлинения надо прикладывать все большую силу (иногда мышцу в этом отношении сравнивают с вязаными вещами: если растягивать, скажем, трикотажный шарф, то вначале он легко изменяет свою длину, а затем становится практически нерастяжимым).
Если мышцу растягивать повторно через небольшие интервалы Времени, то ее длина увеличится больше, чем при однократном «содействии. Это свойство мышц широко используется в практике при выполнении упражнений на гибкость (пружинистые движения, повторные махи и т.п.).
Длина, которую стремится принять мышца, будучи освобожденной от всякой нагрузки, называется равновесной (или свободной). При такой длине мышцы ее упругие силы равны нулю. В живом организме длина мышцы всегда несколько больше равновесной и поэтому даже расслабленные мышцы сохраняют некоторое натяжение.
Для мышц характерно также такое свойство, как релаксация – снижение силы упругой деформации с течением времени. При отталкивании в прыжках с места сразу после быстрого приседания прыжок будет выше, чем при отталкивании после паузы в низшей точке подседа: после паузы упругие силы, возникшие при быстром приседании, вследствие релаксации не используются.
Date: 2015-09-24; view: 1053; Нарушение авторских прав