
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Максимизация прибыли
|
|
Систематическое получение прибыли является необходимой целью предпринимательской деятельности любого предприятия. Поэтому доминирующей проблемой для предприятия является максимизация прибыли, что означает разработку стратегии на систематическое увеличение прибыли и минимизацию издержек. Данная задача многоплановая, вот почему для своего решения она требует системного подхода.
Для принятия решений часто требуется знать сумму прибыли, которую получает предприятие в расчете на единицу продукции при данном объеме реализации и цене, диктуемой спросом. При определении продажной цены используют среднюю прибыль (An) и предельную прибыль (Мn):
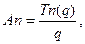 (19.1)
(19.1)
где Tn(q) — совокупная сумма прибыли на определенный товар за определенный период;
q — объем продаж.
Из этого следует, что максимизация прибыли связана с процессом приращения предпринимательской прибыли. Это, в свою очередь, означает, что в расчетах требуется использование предельных величин: предельной прибыли, предельного дохода и предельных издержек. Иными словами, прибыль максимизируется в точке, в которой любое, даже малое приращение объема реализации (выпуска) продукции оставляет прибыль без изменения, т.е. приращение прибыли при приращении объема (реализации) продукции равняется нулю. Математически это можно записать так:
Mn(q)=MR(q) – MC(q) = 0, (19.2)
где Mn(q) — предельная прибыль от объема продукции;
MR(q) — предельный доход (выручка) от объема продукции;
МС(q) — предельные издержки от объема продукции.
Из формулы (19.2) следует, что прибыль максимизируется в том случае, когда предельные издержки равны предельному доходу:
MR(q) = MC(q).
Поясним это на примере работы консервного комбината. Данные о выпуске количества консервов, валовых постоянных издержках, относимых на соответствующее производство, валовых переменных издержках, относимых на соответствующий выпуск продукции, валовых издержках производства и обращения, а также результаты расчета средних и предельных издержек, указанные в тысячах рублях на единицу изделия, приведены в табл. 19.1 (цифры для удобства округлены).
Таблица l9.1
Расчет максимальной прибыли в зависимости от объема продукции, цены и издержек
| Количество изделий | Цена (руб./шт.), Р | Валовый доход (выручка) (тыс. руб.), TР | Валовые издержки (тыс. руб.), ТС | Валовая прибыль (тыс. руб.), М = гр. 3-— гр.4 | Предельный доход (руб./шт.), MR | Предельные издержки (руб./шт.), МС | Предельная прибыль (руб./шт.), Мп |
| -7 | |||||||
| -670 | |||||||
| -268 | -1463 | ||||||
| -436 | -686 | -2381 | |||||
| -5905 | -1104 | -5469 |
Графа 2 табл. 19.1 содержит данные о цене спроса, соответствующие количеству возможной реализации консервов. Функция спроса от цены получена на основе линейного уравнения
q = — 4,78р + 13712,1.
Коэффициент эластичности спроса в зависимости от изменения цены для разного количества продаж исчисляется по формуле:
 (19.3)
(19.3)
В количестве 3000 шт. 
В количестве 6000 шт. 
В количестве 8000 шт, 
При больших объемах продаж спрос становится неэластичным. Предельные величины дохода (выручки), издержек и прибыли получаются путем вычитания из данных валового дохода (гр. 3), валовых издержек (гp. 4) и валовой прибыли (гр. 5) соответствующих значений из предыдущей строки.
Например, предельная прибыль:
для объема продаж 5000 шт.: 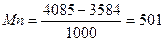 руб.
руб.
для объема продаж 7000 шт.: 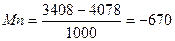 руб.
руб.
Деление на 1000 необходимо потому, что предельные (приростные) показатели определяются в расчете на единицу продукции в рублях.
Для наглядности на основании данных табл. 19.1 построим графики (рис. 19.3 и 19.4).


Из табл. 19.1 и рис. 19.3 и 19.4 следует, что наибольшие объемы реализации не всегда дают наибольшие суммы прибыли. Максимальную сумму прибыли предприятие может получить при объеме реализации более 5 тыс. шт. и менее 6 тыс. шт. банок консервов. При этом цена одной банки составляет примерно 1600 руб. Если количество реализованных банок консервов превышает 6 тыс. шт., то сумма прибыли уменьшается, а при 9 тыс. шт. предприятие понесет убытки в размере 436 тыс. руб., которые при реализации 10 тыс. шт. могут возрасти почти до 6 млн. руб.
Предельные показатели позволяют более четко судить о скорости изменения их значений (рис. 19.4).
Точка пересечения предельного дохода MR(q) с предельными издержками MC(q) определяет максимум прибыли. В этой точке предельная прибыль равна нулю, а ее кривая пересекает ось абсцисс. За данными пределами начинаются убытки, которые будут снижать сумму валовой прибыли.
Для того чтобы решить вопрос максимизации прибыли, важно также знать, действует ли предприятие в условиях свободной конкуренции или монопольного рынка. Пищевые предприятия, в частности, реализуют свою продукцию в условиях свободной конкуренции. А это означает, что за цену реализации своей продукции оно принимает ту, которую задает рынок.
Итак, для предприятия максимизация прибыли заключается в выборе такого объема реализации продукции, при котором предельные издержки предприятия в производстве и при реализации равнялись бы рыночной цене. Математически это можно представить следующим образом:
Р = MC(q). (19.4)
Иными словами, на рынке свободной конкуренции доход равен рыночной цене. Покажем это на примере рыбоперерабатывающего предприятия, выпускающего икру в банках. Данные о производстве, издержках, прибыли, а также о предельных величинах приведены в табл. 19.2.
Таблица 19.2
Экономические показатели и расчеты предельных величин, руб.
| Выпуск банок, шт. | Цена, 1 шт. | Валовой доход (выручка), TR | Валовые издержки, ТС | Прибыль, TR- — TC | Предельный доход (шт.), MR = Р | Предельные издержки (шт.), МС | Предельная прибыль, шт. гр.6— гр.7 |
| -7200 | |||||||
| -4515 | |||||||
| 20 250 | 13 200 | ||||||
| 38 350 | 15 840 | 12 510 | |||||
| 33 750 | 18 000 | 15 750 | |||||
| 36 450 | 19 680 | 16 770 | |||||
| 38 880 | 21 312 | 17 586 | |||||
| 41 175 | 22 920 | 18 255 | |||||
| 45 525 | 24 360 | 18 165 | -9 | ||||
| 42 660 | 24 510 | 18 150 | -15 | ||||
| 42 795 | 24 672 | 18 123 | -27 | ||||
| 42 930 | 24 852 | 18 078 | -45 | ||||
| 43 065 | 25 056 | 18 009 | -69 | ||||
| 43 200 | 25 296 | 17 904 | -105 |
Из табл. 19.2 следует, что предельный доход равен цене одной банки икры при приращении количества реализации в разных размерах (сравним графы 6 и 2). Иными словами, рыночная цена задается рынком (135 руб. за банку икры). Отличительная черта изменения валового дохода (выручки) от реализации банок икры на рынке свободной конкуренции состоит в том, что валовой доход выражается линейным уравнением с нулевым свободным членом и угловым коэффициентом, равным цене одной банки:
TR = 135 руб. q шт. = TR руб.
Максимальная прибыль получается при объемах реализации около 310 банок. По данным табл. 19.2 она составляет 18 255 руб. при реализации 305 банок. В интервале 305 — 315 банок предельная прибыль равна нулю. При дальнейшем росте объема реализации она становится отрицательной, т.е. каждая дополнительная единица приращения объема выпуска дает не увеличение, а уменьшение суммы прибыли (рис. 19.5).

Таким образом, при заданной рынком цене одной банки в размере 135 руб. предприятию выгоднее поддерживать реализацию на уровне, близком к 310 банкам. В этом случае оно может рассчитывать на получение наибольшей суммы прибыли.
Date: 2015-09-22; view: 1131; Нарушение авторских прав