Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Подготовка к срезовой контрольной работе по информатике
1) Представить предложенное число в двоичной/шестнадцатиричной системе счисления и выполнить проверку:
Вариант X
Представить число 2810 в двоичной СС и выполнить проверку.
Перевод числа 28 из десятичной СС в двоичную СС выполняется путем последовательного деления числа на 2 до тех пор, пока частное не станет равно 1:
Затем выписываем последнее частное и остатки от деления (по стрелке) 2810 = 111002 Проверка выполняется обратным переводом из двоичной СС в десятичную СС (сопоставляем цифры двоичного числа и степени 2, затем цифру и соответствующую степень перемножаем и все складываем):
| Вариант Y
Представить число 9110 в шестнадцатиричной СС и выполнить проверку.
Перевод числа 91 из десятичной СС в шестнадцатиричную СС выполняется путем последовательного деления числа на 16 до тех пор, пока частное не станет меньше 16:
Затем выписываем последнее частное и остатки от деления (по стрелке), остаток 10 – A, остаток 11 – B, остаток 12 – C, остаток 13 – D, остаток 14 – E, остаток 15 – F: 9110 = 5B16 Проверка выполняется обратным переводом из шестнадцатиричной СС в десятичную СС (сопоставляем цифры шестнадцатиричного числа и степени 16, затем цифру и соответствующую степень перемножаем и все складываем):
|
28
80
2) Решить задачу (содержательный подход к измерению информации):
| Вариант X Задача. В мешке лежат 32 бумажки с разными пожеланиями. Какое количество информации получено после того, как одну из бумажек достали из мешка? Решение: С одинаковой вероятностью можно вытащить любую из 32 бумажек. Количество вариантов события «бумажку достали из мешка» = количеству бумажек, 32. Количество вариантов развития события (N) и количество информации о том, что один из вариантов «сыграл» (I), связаны формулой: N = 2I. Соответственно: 32 = 2I 25 = 2I I = 5 бит Ответ: количество информации о том, что из мешка достали одну из бумажек = 5 бит. | Вариант Y Задача. Сообщение о том, что начальник приедет проверять магазин №3 в составе торговой сети, содержит 3 бит информации. Сколько магазинов в составе сети? Решение: С одинаковой вероятностью начальник может приехать проверять любой из магазинов. Количество вариантов события «начальник приедет проверять магазин №…» = количеству магазинов. Количество вариантов развития события (N) и количество информации о том, что один из вариантов «сыграл» (I), связаны формулой: N = 2I. Соответственно: N = 23 N = 8 Ответ: 8 магазинов в составе торговой сети. |
3) Решить задачу (измерение объема растровых изображений).
Вариант X
Задача. Разрешение изображения составляет 256x256 точек, глубина цвета (I) – 8 бит. Каков объем данного изображения (N) (ответ записать в Кбайт)?
Решение:
Количество точек, составляющих изображение = 256*256 = 65536.
Каждая точка (а точнее, ее цвет) кодируется 8 битами, следовательно, объем изображения:
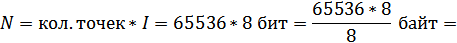
Ответ: объем изображения равен 64 Кбайт.
| Вариант Y
Задача. Разрешение изображения составляет 512x128 точек, объем изображения (N) – 24 Кбайт. Какова глубина цвета (I) данного изображения?
Решение:
Количество точек, составляющих изображение = 512*128 = 65536.
Каждая точка (а точнее, ее цвет) кодируется одинаковым количеством бит, а общий объем изображения
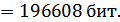 Тогда глубина цвета:
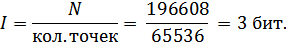Ответ: глубина цвета данного изображения равна 3 бит.
|
4) Определение растрового и векторного изображения.
5) Цветовые модели и области их применения.
6) Аналоговая и дискретная звукозапись.
7) Определение алгоритма и основных алгоритмических структур.
8) Определение и основные функции материнской платы, центрального процессора, оперативной памяти, кэш-памяти.
9) Основные виды накопителей и физические принципы, лежащие в основе их работы.
10) Определение клавиатуры, мыши, трекбола, сенсорной панели, сканера, графического планшета.
11) Определение монитора, видеоподсистемы компьютера; виды принтеров, принципы их работы и типы красящих веществ.
Date: 2015-09-22; view: 445; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |