Методические указания. Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явления

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явления. Необходимо учитывать и разброс или вариацию значений отдельных единиц.

Основными показателями, характеризующими вариацию, являются: размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Размах вариации – простейший показатель, разность между максимальным и минимальным значениями признака.

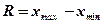
Недостатком является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.

Дисперсия – средний квадрат отклонений значений признака от их средней величины и определяется по формулам простой и взвешенной средней величины.

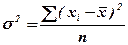и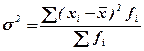

Наиболее удобным и широко распространенным на практике показателем является среднее квадратическое отклонение. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность, что и изучаемый признак.

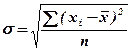и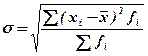

Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемой совокупности. В отличие от них, коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня, что во многих случаях является предпочтительнее:

Если коэффициент вариации не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.

Показатели вариации могут быть использованы не только в анализе изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е.е в анализе взаимосвязей между показателями.

При проведении такого анализа совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным и результативным.

Для выявления взаимосвязи исходная совокупность делится на две или более групп по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:

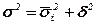
- общая дисперсия;

- средняя из внутригрупповых дисперсий;

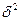- межгрупповая дисперсия.

Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней:

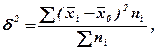
где 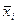- среднее значение результативного признака по i-ой группе;

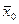- общая средняя по совокупности в целом;

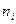- объем (численность) i-ой группы.

Если факторный признак, по которому производится группировка, не оказывает никакого влияния на результативный признак, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая средняя будет равна нулю.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:

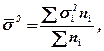
где - дисперсия результативного признака в i-ой группе;

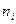- объем (численность) i-ой группы;

Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

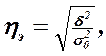
Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

Среди множества варьирующих признаков, изучаемых статистикой, существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Альтернативный признак принимает всего два значения – 0 и 1 с весами соответственно p и q. Поэтому среднее значение альтернативного признака равно р. А дисперсия альтернативного признака равна pq. Дисперсия альтернативного признака равна произведению доли признака, обладающего характеристикой на долю признака, не обладающего характеристикой. Предельное значение дисперсии для альтернативного признака равно 0,25 при р=0,5.

Дисперсия альтернативного признака широко применяется в выборочном обследовании.

Изменения частот в вариационных рядах изменяются закономерно в связи с изменением варьирующего признака. Такие закономерности называются закономерностями распределения.

Основная задача анализа вариационных рядов заключается в выявлении подлинной закономерности распределения путем исключения влияния второстепенных, случайных для данного распределения факторов.

Если увеличить объем совокупности и уменьшить интервал в группах, то графическое изображение приближается к некоторой плавной кривой, которая называется кривой распределения.

Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.

Теоретическая кривая распределения – кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для него факторов.

Выяснение общего характера распределения предполагает оценку его однородности, а также расчет показателей асимметрии и эксцесса.

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии:

Его величина может быть положительной (для правосторонней асимметрии) и отрицательной (для левосторонней асимметрии).

Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной. Если асимметрия меньше 0,25, она считается незначительной.

Если коэффициент асимметрии находится в интервале от 0,25 до 0,5, то наличие асимметрии в генеральной совокупности проверяется с помощью определения оценки существенности на основе средней квадратической ошибки:

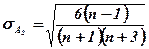
В случае, если 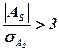, асимметрия считается существенной и распределение признака в генеральной совокупности несимметрично и неслучайно, а закономерно.

Для симметричных распределений может быть рассчитан показатель эксцесса, который показывает, насколько резкий скачок имеет изучаемое явление. Показатель эксцесса определяется на основе центрального момента четвертого порядка по формуле:

Если показатель эксцесса больше нуля, то распределение островершинное и скачок считается значительным, если коэффициент эксцесса меньше нуля, то распределение считается плосковершинным и скачок считается незначительным. Среднеквадратическая ошибка эксцесса показывает, насколько существенен скачок в явлении и рассчитывается по формуле:

К структурным характеристикам ряда распределения относятся мода, медиана, квартили, децили и перцентили.

Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль первого порядка (нижний квартиль) и квартиль третьего порядка (верхний квартиль). Каждый из них отсекает соответственно ¼ и ¾ совокупности. Для расчета квартилей используются следующие формулы:

Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль отсекает 1/10 часть совокупности, а девятый дециль отсекает 9/10 частей. Рассчитываются децили по аналогичным формулам:

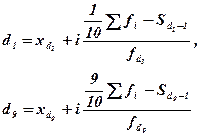
Перцентили – варианты, которые делят ранжированную совокупность на 100 частей.

Date: 2015-09-22; view: 645; Нарушение авторских прав