Методические указания. Средняя величина представляет собой обобщенную количественную характеристику признака статистической совокупности в конкретных условиях места и времени

Средняя величина представляет собой обобщенную количественную характеристику признака статистической совокупности в конкретных условиях места и времени.

Показатель в форме средней величины отражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков.

Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных факторов.

Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности.

На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

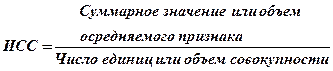
В зависимости от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение.

Различают следующие виды средней, каждая из которых может быть простой и взвешенной:

· Средняя арифметическая;

· Средняя гармоническая;

· Средняя геометрическая;

· Средняя квадратическая, кубическая и т.д.

· Структурные средние: мода и медиана.

Средняя арифметическая простая (не взвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.

Средняя арифметическая взвешенная. При расчете средних величин отдельные значения признака могут повторяться, встречаться по нескольку раз. В данном случае расчет проводится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.

Средняя арифметическая величина имеет следующие свойства, использование которых упрощает ее расчет.

1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты.

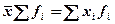
2. Сумма отклонений индивидуального значения признака от средней арифметической равна нулю:

3. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на туже величину.

4. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя соответственно уменьшится или увеличится в А раз:

5. Если все частоты уменьшить или увеличить в А раз, то средняя останется неизменной:

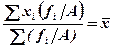
6. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

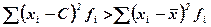
Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Различают среднюю гармоническую простую и взвешенную.

Средняя гармоническая простая.

Средняя гармоническая взвешенная применяется тогда, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.

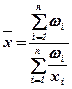
Средняя арифметическая и средняя гармоническая величины могут применятся в одних и тех же ситуациях, но по разным данным. Если в ИСС неизвестен числитель, то в расчетах применяется средняя арифметическая величина. Если в ИСС неизвестен знаменатель, то в расчетах используется средняя гармоническая величина.

Средняя квадратическая величина применяется тогда, когда вместо индивидуальных значений признака представлены квадраты исходных величин.

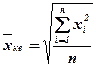
Средняя геометрическая применяется в случаях определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям.

Характеристиками структуры совокупности являются следующие структурные средние:

1. Мода (Mo) – величина признака, наиболее часто встречающаяся в совокупности, т.е. имеющая наибольшую численность в ряду распределения.

а) В дискретном ряду распределения мода определяется визуально.

б) В интервальном ряду распределения визуально можно определить только интервал, в котором заключена мода, который называется модальным интервалом. Мода будет равна:

где х_Мо – нижняя граница модального интервала;

i_Мо – величина модального интервала;

f_Мо – частота модального интервала;

f_Мо-1 – частота, предшествующая модальному интервалу;

f_Мо+1 – частота интервала, следующего за модальным.

2. Медиана (Me) – значение признака, приходящееся на середину ранжированного ряда, т.е. делящее ряд распределения на две равные части.

а) В дискретном ряду распределения определяется номер медианы по формуле:

Номер медианы показывает то значение показателя, которое и является медианой.

б) В интервальном ряду распределения медиана рассчитывается по следующей формуле:

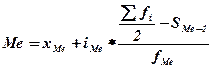
где х_Ме – нижняя граница медианного интервала;

i_Ме – величина медианного интервала;

f_Ме – частота медианного интервала;

S _Ме-1 – сумма накопленных частот, предшествующих медианному интервалу;

åf_i/2 – полусумма частот ряда.

Мода и медиана могут быть определены графически.

Date: 2015-09-22; view: 734; Нарушение авторских прав