Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод Ньютона
|
|
Алгоритм минимизации целевой функции (1.1) по методу Ньютона предусматривает итерационный процесс
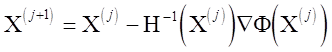, (2.7)
где Х(j) — вектор неизвестных в j-ом приближении;
, (2.8)
Матрица Гессе вторых частных производных, взятых в точке Х(j), а градиент целевой функции имеет выражение
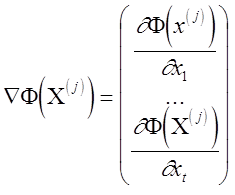. (2.9)
Применим алгоритм Ньютона к целевой функции метода наименьших квадратов
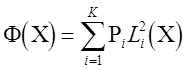, (2.10)
где Рi — веса измерений.
В этом частном случае для градиента целевой функции в символах Гаусса получим
.
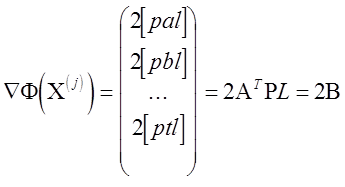где А - матрица коэффициентов уравнений поправок;
Р - диагональная матрица весов измерений;
L. - вектор свободных членов уравнений поправок.
Зная первые частные производные целевой функции (2.10), получим вторые частные производные и в символах Гаусса применительно к матрице (2.8) запишем
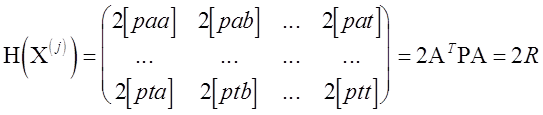
Окончательно вместо (2.7), сокращая двойки, в матричной форме получим
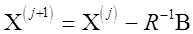, (2.11)
что соответствует алгоритму Гаусса.
Отметим, что метод Гаусса, определяемый матричным выражением (2.11), есть частный случай метода Ньютона, описываемого выражением (2.7), поскольку последний применим не только для целевой функции (2.10), но и для других целевых функций. Поэтому алгоритм (2.11) в математической литературе еще называют методом Ньютона-Гаусса. Объединяет эти два метода общий недостаток: в методе Ньютона используется линеаризация при вычислении численным способом первых и вторых частных производных критериальной функции, в методе Гаусса также используется линеаризация при вычислении элементов матрицы А.
Для численного определения по параметрам первых частных производных целевой функции, входящих в (2.9), используют формулы (2.3) - (2.5).
Вторые смешанные частные производных можно вычислить по известной формуле численного дифференцирования
,
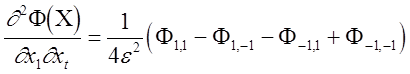где значения целевой функции определяются в точках, показанных на рис. 2.5.
Вторые квадратичные частные производные можно найти по формуле
,
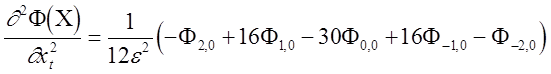где значения целевой функции вычисляются в точках, показанных на рис. 2.6.
Рис. 2.5. Расположение точек для численного определения
смешанных вторых частных производных
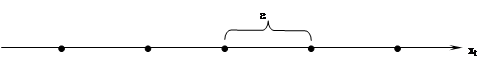- 2,0 -1,0 0,0 1,0 2,0
|
Рис. 2.6. Расположение точек для численного определения
Date: 2015-09-26; view: 490; Нарушение авторских прав