Логические основы и элементная база ЦВМ

При обработке двоичных кодов вычислительная машина выполняет некоторые преобразования над их изображениями (наборами сигналов), в процессе которых образуются новые наборы сигналов, интерпретируемые как результаты операций. В устройствах, выполняющих указанные функциональные преобразования, в качестве входной информации используются обрабатываемые двоичные коды, а в качестве выходной - генерируются новые коды (результаты обработки).

Поскольку переменные и функции от них, принимающие только два значения (0 или 1), называют логическими, а двоичные коды, являющиеся объектами обработки в вычислительных машинах, представляют собой последовательности двоичных цифр, поступающие на обработку отдельные разряды этих кодов можно рассматривать как логические переменные, а полученные результаты - как логические функции.

Для связи простых переменных в выражениях (образования логических функций) используются знаки логических связей (знаки логических операций), составляющие аппарат алгебры логики - науки, которая формулирует правила действий над логическими переменными.

Рассмотрим некоторые из логических операций, широко используемых в теории ЦВМ для описания функционирования отдельных элементов аппаратуры и алгоритмов работы построенных на их базе устройств.

Операция отрицания реализует действие, называемое инверсией и заключающееся в изменении значения аргумента на противоположное, обозначается чертой над аргументом этой операции (читается как НЕ). Так, если А = 1, то , если А = 0, то 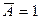. Функциональный элемент, реализующий операцию отрицания, называется инвертором, или схемой НЕ. Наборы таких элементов необходимы, например, для генерации дополнительных или обратных кодов отрицательных двоичных чисел.

Операция логического умножения, или конъюнкция, позволяет образовать логическую функцию, принимающую значение, равное единице, только тогда, когда все ее аргументы равны единице. Логическая связь этого типа обозначается символом 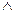который читается как И. Значение конъюнкции любого числа аргументов определяется с помощью таблицы логического умножения, имеющей вид:

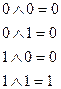
Отсюда можно получить ряд обобщений: 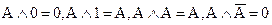, используемых для упрощения выражений, содержащих более двух аргументов. Функциональный элемент, реализующий конъюнкцию аппаратно, называется схемой совпадения.

Операция логического сложения, или дизъюнкция, используется для образования логической функции, принимающей значение, равное нулю, только тогда, когда все ее аргументы также равны нулю. Такая логическая связь обозначается символом 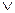, который читается как ИЛИ. Значение дизъюнкции любого числа аргументов определяется с помощью таблицы логического сложения, имеющей вид:

На основании таблицы легко выводятся следующие обобщения: 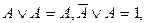являющиеся основой для упрощения выражений, содержащих несколько аргументов. Функциональный элемент, аппаратно реализующий дизъюнкцию, называется собирательной схемой.

Операции логического умножения и сложения, подобно операциям алгебраического сложения и умножения, подчиняются переместительному, сочетательному и распределительному законам. На основании этих правил и указанных выше обобщений осуществляются преобразования и упрощения сложных логических зависимостей, содержащих функции типа И, ИЛИ и НЕ.

В алгебре логики используются и другие типы функций, однако можно доказать, что любые из них могут быть представлены как некоторые комбинации функций типа И, ИЛИ и НЕ, называемых поэтому основными. Это означает, что технические устройства, реализующие сколь угодно сложные операции преобразования данных, могут быть построены из элементов, реализующих лишь основные логические функции.

В качестве таких элементов в настоящее время в подавляющем большинстве случаев используются электронные схемы. Поэтому современные цифровые вычислительные машины получили название электронных вычислительных машин (ЭВМ) и в дальнейшем мы будем называть их именно так.

В качестве аргументов, поступающих на входы электронных схем, используются комбинации электрических сигналов, изображающие подлежащие преобразованию данные. При этом на выходах таких схем должны появляться комбинации выходных электрических сигналов, изображающие результаты выполненных преобразований.

Характеристика таких сигналов зависит от типа используемых для построения схем элементов и здесь не рассматривается. Для удобства изложения будем далее считать, что отсутствие сигнала изображает двоичный код нуль, а его присутствие - двоичный код единица.

Не вдаваясь в детали технической реализации логических схем, перечислим основные из них и рассмотрим приемы использования аппарата алгебры логики для описания и проектирования этих устройств.

Инвертор - схема, реализующая операцию отрицания (схема НЕ). Схема инвертора работает следующим образом: если сигнал на входе схемы отсутствует (код нуля), то на ее выходе есть сигнал (код единицы), и наоборот.

Схема совпадения, реализующая операцию И. Код единицы на выходе такой схемы может появиться только в том случае, если на всех ее входах одновременно присутствуют коды единицы.

Собирательная схема, реализующая операцию ИЛИ. Код нуля на выходе схемы может появиться только тогда, когда на всех ее входах одновременно присутствуют коды нуля.

Схемы И, ИЛИ и НЕ являются теми «кирпичиками», из которых строится все «здание» ЭВМ. Каким же образом осуществляется проектирование на этой элементной базе более крупных составляющих машин: блоков, узлов и устройств? Основой для такого проектирования является математический аппарат алгебры логики.

Вначале в соответствии с назначением проектируемого узла составляют таблицы, связывающие наборы его входных и выходных сигналов. Затем с помощью аппарата алгебры логики составляют логические формулы, описывающие указанные связи. После анализа и упрощения формул (если это возможно) на основании содержащихся в них логических функций создают структурную схему будущего узла. Для получения принципиальной схемы такого узла необходимо заменить каждый элемент структурной схемы конкретным физическим элементом, реализующим соответствующую операцию.

Вначале технология изготовления элементов для ЭВМ заключалась в сборке и соединении отдельных электронных компонентов в форме так называемых плат. Этот метод продолжал оставаться основным и при появлении миниатюрных элементов (микроэлементов), из которых компоновали микромодули - миниатюрные электронные схемы стандартной формы и заданного назначения.

Затем, благодаря новейшим достижениям физики, химии, электроники и кибернетики, появилось новое направление - создание объединенных в одно целое наборов функционально связанных между собой элементов - интегральных схем. Технология создания схем такова, что изготовление входящих в них элементов совмещено с установлением связей между ними, в результате чего получают функционально полные интегральные микросхемы с заранее заданными свойствами.

Это позволило упростить изготовление схем и в сотни тысяч раз увеличить плотность упаковки элементов. Такие схемы, называемые большими интегральными, представляют собой многофункциональные устройства, позволившие не только существенно улучшить характеристики ЭВМ, но и по новому подойти к проектированию вычислительных систем.

Date: 2015-09-26; view: 593; Нарушение авторских прав