
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Химические превращения
|
|
Термодинамика химических реакций.
Уравнение химической реакции (стехиометрическок уравнение):
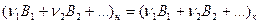 . (1)
. (1)
Bi - символы химических формул реагирующих веществ,
ni - стехиометрические коэффициенты.
Каждая химическая формула в уравнении реакции изображает 1 кмоль соответсвующего вещества; индекс «н» указывает начальные (исходные) вещества, индекс «к» - конечные вещества (продукты реакции). Таким образом, в левой части стехиометрического уравнения указываются вещества, количества которых в ходе реакции уменьшаются, а в правой части - вещества, возникающие в результате реакции.
Стехиометрические коэффициенты показывают, в каких соотношениях изменяются количества молей веществ в химической реакции. Правило знаков стехиометрических коэффициентов: ni н < 0, ni к > 0 (в литературе по термодинамике может встретиться противоположное правило знаков).
Вещества, участвующие в химической реакции, называются составляющими реакции. Мы будем рассматривать реакции при условии, что все ее составляющие являются идеальными газами.
Мера реакции. Пусть протекает химическая реакция
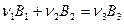 .
.
В некотором состоянии 1 в реакторе было 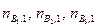 кмоль реагирующих веществ, а в состоянии 2
кмоль реагирующих веществ, а в состоянии 2 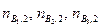 кмоль. Изменения количеств реагирующих веществ в реакции будут
кмоль. Изменения количеств реагирующих веществ в реакции будут 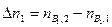 ,
, 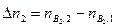 и
и 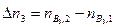 . При химических превращениях изменения количеств реагирующих веществ пропорциональны соответствующим стехиометрическим коэффициентам:
. При химических превращениях изменения количеств реагирующих веществ пропорциональны соответствующим стехиометрическим коэффициентам:
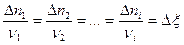 , кмоль (2)
, кмоль (2)
или в дифференциальной форме
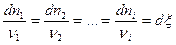 , кмоль. (3)
, кмоль. (3)
Коэффициент пропорциональности  или
или 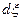 в этом уравнении называется мерой реакции (иногда числом пробегов реакции). Этот коэффициент характеризует степень изменения состава системы при химической реакции. Мера реакции является величиной, общей для всех составляющих химической реакции.
в этом уравнении называется мерой реакции (иногда числом пробегов реакции). Этот коэффициент характеризует степень изменения состава системы при химической реакции. Мера реакции является величиной, общей для всех составляющих химической реакции.
Выразим через меру реакции изменение количества вещества в реакции:
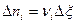 или
или 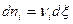 , кмоль.
, кмоль.
О работе, получаемой за счет химической энергии. Запишем два выражения дифференциала внутренней энергии:
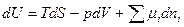 , кДж
, кДж
и
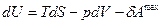 , кДж.
, кДж.
Здесь 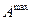 - максимальное количество немеханической работы. Немеханическая работа имеет максимальное значение, если химическая реакция осуществляется термодинамически обратимо.
- максимальное количество немеханической работы. Немеханическая работа имеет максимальное значение, если химическая реакция осуществляется термодинамически обратимо.
Химическая реакция называется термодинамически обратимой, если в каждом ее состоянии соблюдается внутреннее и внешнее термодинамическое равновесие, т.е. температуры и давления всех составляющих реакции одинаковы (внутреннее равновесие) и одинаковы температуры и давления реагирующей смеси и окружающей среды (внешнее равновесие). Условием термодинамической обратимости реакции является бесконечно медленное её проведение, т.е. проведение её бесконечно малыми шагами от одного состояния равновесия к следующему, бесконечно близкому предыдущему.
Хотя обратимые процессы возможны только теоретически, но мы вправе рассматривать реакцию как термодинамически обратимую, поскольку на практике к обратимому проведению реакции можно приблизиться и иногда с высокой точностью. Например, в лабораторных условиях возможно практически обратимо проводить химическую реакцию в гальванических элементах. Если сопротивлние внешней цепи гальванического элемента настолько велико (а следовательно, сила тока настолько мала), что выделяющейся в цепи джоулевой теплотой можно пренебречь, то прохождение тока и вызывающую его химическую реакцию можно считать обратимыми.
Сравнивая между собой приведенные выше выражения дифференциала внутренней энергии, получаем:
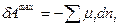 , (4)
, (4)
где 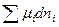 - изменение химической энергии системы. Следовательно, за счет изменения химической энергии системы может быть получена немеханическая работа; знак «минус» означает, что при совершении немеханической работы химическая энергия уменьшается.
- изменение химической энергии системы. Следовательно, за счет изменения химической энергии системы может быть получена немеханическая работа; знак «минус» означает, что при совершении немеханической работы химическая энергия уменьшается.
Чтобы представить себе, как получается, что химическая энергия системы превращается в работу, возьмем для примера гальванический элемент. При протекании в нем химической реакции во внешней цепи возникает электрический ток, который может совершить работу.
Тепловые эффекты химической реакции. Раздел химической термодинамики, в котором рассматриваются тепловые эффекты реакций, называется термохимией. Этот раздел основывается на первом законе термодинамики. Химические превращения принято рассматривать при условии постоянства в системе либо температуры и объема 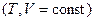 , либо температуры и давления
, либо температуры и давления 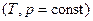 , поэтому тепловые эффекты рассматриваются именно для этих условий.
, поэтому тепловые эффекты рассматриваются именно для этих условий.
Запишем в конечной форме выражения для изменения внутренней энергии и энтальпии в химической реакции (уравнения первого закона термодинамики):
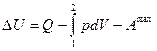 ,
,
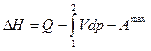 .
.
Здесь 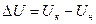 и
и 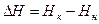 - разность внутренних энергий и разность энтальпий продуктов реакции и исходных веществ.
- разность внутренних энергий и разность энтальпий продуктов реакции и исходных веществ.
Если немеханическая работа не производится, а протекает химическая реакция, то из этих уравнений получим:
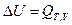 и
и 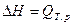 , кДж.
, кДж.
Эти величины называются тепловыми эффектами химической реакции при соответствующих условиях.
Определение. Тепловым эффектом химической реакции называется количество теплоты, выделяемое или поглощаемое системой при неизменных 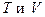 или
или 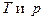 и при условии, что системой не производится немеханическая работа.
и при условии, что системой не производится немеханическая работа.
Реакции, сопровождающиеся выделением теплоты, называются экзотермическими, а реакции, в которых теплота поглощается, эндотермическими. В первом случае теплота должна быть отведена от системы для поддержания 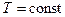 , а во втором - с той же целью теплота должна быть подведена к системе. В соответствии с правилом знаков, принятых для количества теплоты, тепловой эффект экзотермической реакции отрицателен, а тепловой эффект эндотермической реакции положителен. Будем обозначать тепловые эффекты символами
, а во втором - с той же целью теплота должна быть подведена к системе. В соответствии с правилом знаков, принятых для количества теплоты, тепловой эффект экзотермической реакции отрицателен, а тепловой эффект эндотермической реакции положителен. Будем обозначать тепловые эффекты символами 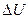 при
при  и
и 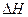 при
при 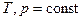 . Тепловой эффект
. Тепловой эффект 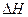 иногда называют изменением энтальпии реакции или просто энтальпией реакции.
иногда называют изменением энтальпии реакции или просто энтальпией реакции.
Найдем связь между тепловыми эффектами 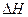 и
и 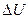 . Значения энтальпии в начальном и конечном состояниях системы:
. Значения энтальпии в начальном и конечном состояниях системы:
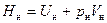 и
и 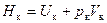 .
.
Разность энтальпий:
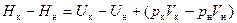 .
.
При 
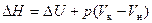 ,
,
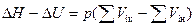 .
.
Перепишем последнее выражение, применив к i -тым составляющим реакции уравнение состояния идеального газа 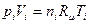 . В этом уравнении p, Па, V, м3, n, кмоль, T, К,
. В этом уравнении p, Па, V, м3, n, кмоль, T, К, 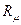 , Дж/(моль.К).
, Дж/(моль.К).
Из уравнения состояния 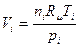 . Реакция протекает в условиях
. Реакция протекает в условиях 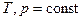 . Следовательно,
. Следовательно,
 .
.
Учитывая, что разность сумм равна сумме разностей, а также выражая изменения количеств составляющих через меру реакции и имея в виду, что величина  для данной реакции постоянна, получим
для данной реакции постоянна, получим
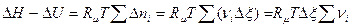 ,
,
где коэффициенты 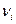 берутся со своими знаками.
берутся со своими знаками.
Получившееся уравнение
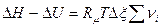 , кДж
, кДж
поделим на меру реакции  кмоль, чтобы перейти к молярным значениям тепловых эффектов:
кмоль, чтобы перейти к молярным значениям тепловых эффектов:
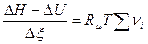 или
или  , кДж/кмоль.
, кДж/кмоль.
Если относить изменение функций состояния к 1 кмоль такой составляющей реакции, стехиометрический коэффициент которой равен единице, получим
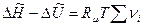 , кДж/кмоль.
, кДж/кмоль.
В дальнейшем будем обозначать молярные величины без знака волны:
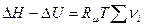 , кДж/кмоль. (5)
, кДж/кмоль. (5)
Термохимическое уравнение. Уравнение химической реакции с указанием значения теплового эффекта называется термохимическим уравнением. Значение теплового эффекта с его знаком указывают в правой части термохимического уравнения, например:
:
СО + 0,5О2 = СО2 - 284000 кДж/кмоль.
В этой реакции тоже получается двуокись углерода, но тепловой эффект этой реакции имеет другое значение. При определении тепловых эффектов по таблицам следует учитывать, что в таблицах указаны тепловые эффекты образования веществ из элементов. Поэтому в таблице мы найдем для теплового эффекта образования СО2 значение - 394000 кДж/кмоль, а не
- 284000 кДж/кмоль.
Закон Гесса. Положение, называемое законом Гесса, установлено в 1840 г. русским химиком Г.И. Гессом. Оно заключается в следующем: тепловой эффект химической реакции зависит только от начального и конечного состояний реакции и не зависит от ее промежуточных стадий.
На основании закона Гесса термохимическими уравнениями можно оперировать как алгебраическими, т.е. можно комбинировать их по своему усмотрению с целью определения теплового эффекта какой-либо стадии реакции.
Пример 1. Известно:
С + 0,5О2 = СО - 110500 кДж/кмоль,
СО + 0,5О2 = СО2 - 284000 кДж/кмоль.
Сложим эти термохимические уравнения и получим:
С + О2 = СО2 - 394000 кДж/кмоль.
Количество теплоты не является функцией состояния: выделяемое или поглощаемое в процессе количество теплоты зависит от характера этого процесса. Но химические реакции наблюдаются в условиях 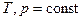 или
или 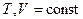 , а в этих случаях, согласно уравнениям 1-го закона термодинамики, количество теплоты выражается разностями функций состояния (соответственно
, а в этих случаях, согласно уравнениям 1-го закона термодинамики, количество теплоты выражается разностями функций состояния (соответственно 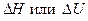 ) и поэтому не зависит от характера процесса.
) и поэтому не зависит от характера процесса.
Пример. Тепловой эффект реакции образования ацетилена С2Н2 из элементов составляет 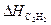 = 226860 кДж/кмоль; тепловые эффекты полного сгорания углерода и водорода соответственно равны -394000 и -242020 кДж/кмоль. Определить тепловой эффект реакции сгорания ацетилена.
= 226860 кДж/кмоль; тепловые эффекты полного сгорания углерода и водорода соответственно равны -394000 и -242020 кДж/кмоль. Определить тепловой эффект реакции сгорания ацетилена.
Решение. Реакция сгорания ацетилена:
С2Н2 + 2.5 О2 = 2СО2 + Н2О + D Н.
Нужно определить DН. Для этого дано: реакция образования ацетилена:
2С + Н2 = С2Н2 + 226860 кДж/кмоль.
Реакции сгорания углерода и водорода:
С + О2 = СО2 - 394000 кДж/кмоль,
Н2 + 0,5 О2 = Н2О – 242000 кДж/кмоль.
Скомбинируем последние три термохимических уравнения так, чтобы при их сложении получалось уравнение сгорания ацетилена:
С2Н2 = 2С + Н2 - 226860
2С + 2О2 = 2СО2 - 2 × 394000
Н2 + 0,5 О2 = Н2О – 242000
-----------------------------------------------
С2Н2 + 2.5 О2 = 2СО2 + Н2О + D Н
Видно, что одну и ту же реакцию можно провести двумя различными путями: первый путь - непосредственное сгорание ацетилена, а второй - поэтапное проведение реакции.
На основании закона Гесса получим:
D Н = –226860 – 2 × 394000 – 242000 = –1256880 кДж/кмоль.
Запишем этот результат в обозначениях:
D Н = –1× 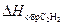 + 2×
+ 2× 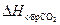 + 1×
+ 1× 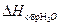 .
.
Это выражение записано через тепловые эффекты образования всех веществ, участвующих в реакции сгорания ацетилена.
Следствие из закона Гесса: тепловой эффект реакции равен алгебраической сумме произведений стехиометрических коэффициентов на тепловые эффекты образования веществ, участвующих в реакции, т.е.
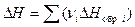 , кДж/кмоль. (6)
, кДж/кмоль. (6)
В этом выражении 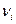 берутся со своими знаками.
берутся со своими знаками.
Это следствие из закона Гесса можно применить и к изохорному тепловому эффекту:
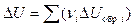 , кДж/кмоль. (7)
, кДж/кмоль. (7)
В таблицах термодинамических величин даются изобарные тепловые эффекты образования веществ при стандартных условиях 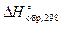 ; эта величина называется стандартной энергией Гиббса образования. Стандартные условия:
; эта величина называется стандартной энергией Гиббса образования. Стандартные условия: 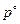 = 1 атм и Т 0 = 298,15 К. Стандартные условия отличаются от введенных ранее нормальных условий значением температуры.
= 1 атм и Т 0 = 298,15 К. Стандартные условия отличаются от введенных ранее нормальных условий значением температуры.
Стандартная энергия Гиббса реакции определяется по формуле:
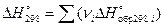 . (8)
. (8)
Поскольку в таблицах не приводятся стандартные энергии Гельмгольца образования веществ, то изохорные тепловые эффекты реакций образования при стандартных условиях определяются по уравнению:
 .
.
Зависимость теплового эффекта реакции от температуры (уравнение Кирхгофа).
Продифференцируем полученные из закона Гесса выражения
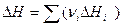 и
и 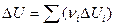
по температуре, первое - при 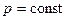 , а второе - при
, а второе - при 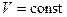 . Получим:
. Получим:
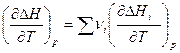 и
и 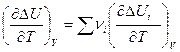 .
.
Так как 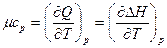 и
и 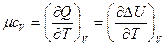 , кДж/кмоль×К,
, кДж/кмоль×К,
то
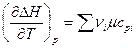 и
и  .
.
Полученные выражения называются уравнениями Кирхгофа. Они выражают зависимость теплового эффекта реакции от температуры. Здесь ni - стехиометрические коэффициенты, которые записываются со своими знаками, а 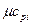 и
и 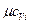 - молярные теплоемкости составляющих реакции.
- молярные теплоемкости составляющих реакции.
Поскольку для идеальных газов внутренняя энергия и энтальпия являются функциями только температуры, то имеем полные производные:
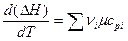 и
и 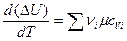 .
.
Используя общее обозначение Q для тепловых эффектов 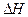 и
и 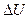 , запишем полученные выражения в обобщенном виде
, запишем полученные выражения в обобщенном виде

и произведем интегрирование:
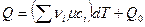 .
.
Здесь Q 0 - постоянная интегрирования. Чтобы выполнить интегрирование, нужно иметь зависимости истинных молярных теплоемкостей составляющих реакции от температуры. Теплоемкости задаются в виде следующих многочленов:
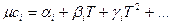
Интегрируя, ограничимся тремя членами этой зависимости и получим:
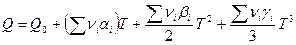 . (1)
. (1)
Постоянную интегрирования Q 0 можно было бы рассматривать как тепловой эффект при  К, но только в том случае, если бы принятые при интегрировании зависимости теплоемкости от температуры были справедливы вплоть до абсолютного нуля. Поскольку это не так, то для определения Q 0 нужно располагать значением теплового эффекта рассматриваемой реакции при какой-либо определенной температуре, для которой используемые зависимости теплоемкостей справедливы, т.е.требуются начальные условия.
К, но только в том случае, если бы принятые при интегрировании зависимости теплоемкости от температуры были справедливы вплоть до абсолютного нуля. Поскольку это не так, то для определения Q 0 нужно располагать значением теплового эффекта рассматриваемой реакции при какой-либо определенной температуре, для которой используемые зависимости теплоемкостей справедливы, т.е.требуются начальные условия.
Примем 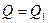 при
при 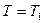 . Получим:
. Получим:
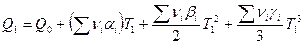 .
.
Выразим отсюда Q 0 и подставим его в уравнение (1):
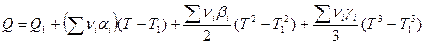 .
.
Пользуясь полученным уравнением, можно выразить и 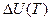 , и
, и 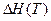 . Перепишем его применительно к изобарному тепловому эффекту
. Перепишем его применительно к изобарному тепловому эффекту 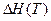 , а начальные условия выберем при стандартных условиях:
, а начальные условия выберем при стандартных условиях: 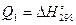 при Т 1 = 298 К. Тогда получим следующую формулу, выражающую зависимость изобарного теплового эффекта реакции от температуры:
при Т 1 = 298 К. Тогда получим следующую формулу, выражающую зависимость изобарного теплового эффекта реакции от температуры:
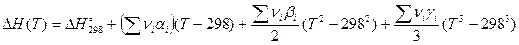 (А)
(А)
Чтобы подставить в эту формулу стандартную энергию Гиббса 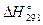 , ее нужно подсчитать по приведенной выше формуле
, ее нужно подсчитать по приведенной выше формуле
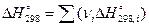 . (В)
. (В)
Значения 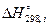 определяются по таблицам стандартных термодинамических величин.
определяются по таблицам стандартных термодинамических величин.
Химическое равновесие.
До тех пор, пока не рассматривались химические превращения, понятия «равновесие» и «обратимость» понимались однозначно. Но при переходе к химическим реакциям необходимо отличать понятия химического равновесия и химической обратимости от понятий термодинамического равновесия и термодинамической обратимости.
Запишем уравнение химической реакции:
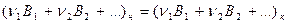 .
.
Перед проведением реакции в реакторе смешиваются начальные вещества (индекс «н»). Такое состояние реакции называется исходным, а состав - исходным составом. Молярный исходный состав реакции будем обозначать прописными буквами: 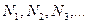 кмоль.
кмоль.
Исходная смесь веществ характеризуеся неоднородностью поля химического потенциала, в силу чего и происходит химическая реакция. В этой стадии реакция является химически неравновесной.
Некоторое время реакция идет в прямом направлении - в сторону образования конечных веществ (индекс «к»). Когда в реакторе появляется некоторое количество конечных веществ, реакция начинает идти не только в прямом, но и в обратном направлении[1], но в прямом интенсивнее, чем в обратном. Постепенно количества начальных веществ уменьшаются, а количества конечных веществ увеличиваются, т.е. на химически
неравновесной стадии реакции ее состав является переменным.
Важно учесть следующее обстоятельство. В действительности ни одна реакция не продолжается до полного израсходования начальных веществ. В каждой реакции при определенных Т и р с течением времени обязательно наступает такое состояние, в котором реакция начинает идти в прямом и обратном направлениях с одинаковой интенсивностью, поэтому ее состав становится постоянным. В этом состоянии реакция называется химически равновесной, а ее состав - равновесным составом. Молярный состав равновесной смеси будем обозначать строчными буквами: 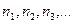 кмоль.
кмоль.
В обеих стадиях - химически неравновесной и химически равновесной - реакция рассматривается как термодинамически обратимая. Понятие термодинамической обратимости процесса было сформулировано выше. Под химической обратимостью понимается возможность протекания реакции как в прямом, так и в обратном направлениях. Любая реакция химически обратима.
Зависимость химического потенциала от давления. Мы будем рассматривать химические реакции, главным образом, в условиях 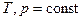 . В этих условях характеристической функцией является энергия Гиббса G.
. В этих условях характеристической функцией является энергия Гиббса G.
Запишем основное уравнение термодинамики для сложной системы через энергию Гиббса:
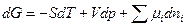 (1)
(1)
С другой стороны, поскольку
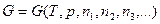 ,
,
то
 . (2)
. (2)
Учитывая, что  и
и 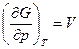 и сравнивая выражения (1) и (2), получаем
и сравнивая выражения (1) и (2), получаем
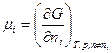 , кДж/кмоль.
, кДж/кмоль.
Продифференцируем это выражение по давлению:
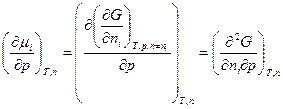 . (3)
. (3)
Так как результат дифференцирования не зависит от порядка дифференцирования, то
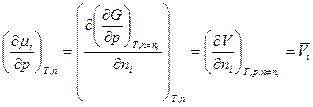 , м3/кмоль.
, м3/кмоль.
Здесь 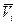 представляет собой парциальный молярный объем i -той составляющей реакции.
представляет собой парциальный молярный объем i -той составляющей реакции.
Таким образом, получено выражение зависимости химического потенциала от давления:
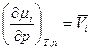 . (4)
. (4)
Химический потенциал составляющей реагирующей смеси идеальных газов. Парциальным называется объем, который занимала бы одна из составляющих смеси, имея давление и температуру смеси. Следовательно, уравнение состояния идеального газа можно записать следующим образом:
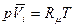 ,
,
откуда парциальный молярный объем
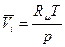 .
.
Подставим это выражение в уравнение (4) и получим
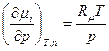
или
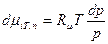 .
.
Если система представляет собой не смесь газов, а один газ, то парциальный молярный объем равен просто молярному объему, т.е. также 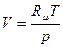 , следовательно, для одного газа можно записать:
, следовательно, для одного газа можно записать:
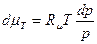 .
.
Проинтегрируем это выражение от некоторого давления 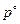 до текущего давления
до текущего давления 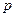 :
:
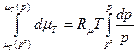 .
.
Получим при 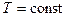 :
:
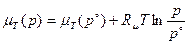 .
.
Поскольку химический потенциал зависит и от температуры, то теперь будем считать температуру не постоянной, а переменной величиной:
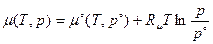 .
.
Здесь 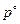 выступает в роли масштаба отнесения давлений. Принимая
выступает в роли масштаба отнесения давлений. Принимая 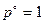 , получаем
, получаем
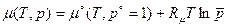 ,
,
где 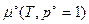 - постоянная интегрирования, представляющая собой химический потенциал газа при данной температуре и давлении
- постоянная интегрирования, представляющая собой химический потенциал газа при данной температуре и давлении 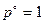 . Под знаком логарифма стоит относительная величина. Эта величина является безразмерной, если давление p и масштаб отнесения
. Под знаком логарифма стоит относительная величина. Эта величина является безразмерной, если давление p и масштаб отнесения 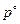 выражаются в одинаковых единицах. Из этого следует, что значение химического потенциала, вычисленное по последнему уравнению, зависит от того, в каких единицах подставляется в это уравнение давление и в каких - масштаб отнесения давления.
выражаются в одинаковых единицах. Из этого следует, что значение химического потенциала, вычисленное по последнему уравнению, зависит от того, в каких единицах подставляется в это уравнение давление и в каких - масштаб отнесения давления.
Если имеется смесь идеальных газов, то каждая составляющая этой смеси характеризуется своими парциальным давлением и химическим потенциалом:
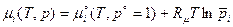 . (5)
. (5) 
В этом выражении  - безразмерное парциальное давление.
- безразмерное парциальное давление.
Условие химического равновесия. Условие химического равновесия установим из условия равновесия сложной системы:
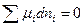 , кДж.
, кДж.
Выразим изменение количества вещества через меру реакции:
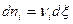 , кмоль
, кмоль
и подставим в условие равновесия сложной системы:
 .
.
Отнеся это уравнение к мере реакции, получим условие химического равновесия
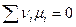 ,
,
которое заключается в том, что сумма произведений химических потенциалов составляющих реакции на их стехиометрические коэффициенты равна нулю.
Закон действующих масс. Подставим в условие химического равновесия выражение (5):
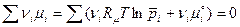
или
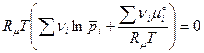 .
.
Отсюда получим:
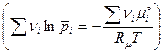 .
.
Очевидно, что
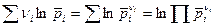 ,
,
следовательно
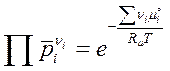 .
.
Видно, что для данной идеально-газовой реакции величина 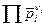 от давления не зависит и при постоянной температуре сохраняет постоянное значение. Эта постоянная величина обозначается
от давления не зависит и при постоянной температуре сохраняет постоянное значение. Эта постоянная величина обозначается 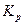 и называется константой химического равновесия. Константа
и называется константой химического равновесия. Константа 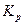 связывает между собой парциальные давления веществ в системе при химическом равновесии.
связывает между собой парциальные давления веществ в системе при химическом равновесии.
С учетом правила знаков стехиометрических коэффициентов можно написать
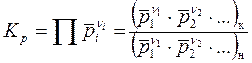 .
.
Поскольку в это выражение входят безразмерные давления, то и константа 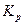 является величиной безразмерной, но ее значение зависит от того, в каких единицах выражается давление.
является величиной безразмерной, но ее значение зависит от того, в каких единицах выражается давление.
Можно написать подобное выражение не только через безразмерные парциальные давления 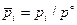 , но также через безразмерные концентрации
, но также через безразмерные концентрации 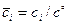 составляющих реакции, где
составляющих реакции, где 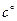 - масштаб отнесения концентраций:
- масштаб отнесения концентраций:
 .
.
Видно, что и  - величина безразмерная. Так как парциальные давления связаны с молярно-объемными концентрациями выражением
- величина безразмерная. Так как парциальные давления связаны с молярно-объемными концентрациями выражением 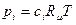 , то можно сделать заключение, что величина
, то можно сделать заключение, что величина  при постоянной температуре так же, как
при постоянной температуре так же, как 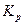 , величина постоянная (независящая от давления).
, величина постоянная (независящая от давления).
Сформулируем закон действующих масс:
В состоянии химического равновесия произведение концентраций или парциальных давлений реагирующих веществ в степенях, равных их стехиометрическим коэффициентам, есть величина постоянная при заданной температуре.
Получим соотношение между константами равновесия 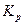 и
и  . Поскольку
. Поскольку
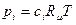 ,
, 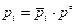 и
и 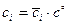 ,
,
то
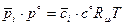 .
.
Отсюда
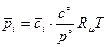 ,
,
следовательно,
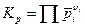 =
= 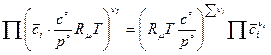
и
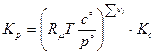 .
.
Можно записывать константы равновесия и через другие безразмерные характеристики состава системы:
через молярные доли: 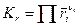 ;
;
через количество вещества: 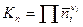 .
.
Все соотношения: 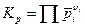 ,
, 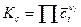 ,
, 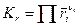 и
и 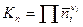 выражают закон действующих масс. Учитывая, что
выражают закон действующих масс. Учитывая, что 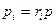 , откуда
, откуда 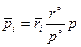 и что
и что 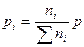 , откуда
, откуда 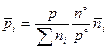 , получим еще две формулы связи между константами равновесия:
, получим еще две формулы связи между константами равновесия:
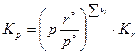 и
и 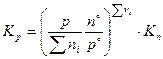 .
.
Здесь 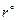 и
и 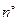 - масштабы отнесения соответствующих характеристик состава системы.
- масштабы отнесения соответствующих характеристик состава системы.
По полученным формулам видно, что константы 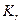 и
и 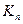 зависят от давления, при котором протекает химическая реакция, т.е. в отличие от
зависят от давления, при котором протекает химическая реакция, т.е. в отличие от 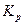 и
и  , сохраняющих постоянное значение при
, сохраняющих постоянное значение при 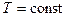 и любом давлении,
и любом давлении, 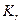 и
и 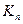 постоянны при
постоянны при 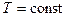 и
и  .
.
Константа равновесия как характеристика полноты реакции. Химическая реакция называется полной, если в смеси присутствуют только продукты реакции, а начальные вещества израсходованы. Но, как уже было сказано, реакция достигает состояния равновесия еще до израсходования всех начальных веществ.
Равновесному состоянию реакции может соответствовать разная степень полноты. В одних случаях состояние равновесия может быть таким, что в реагирующей смеси присутствует больше продуктов реакции, чем начальных веществ, а в других - наоборот. О степени полноты реакции можно судить по значению константы равновесия.
Запишем, например, выражение константы равновесия 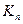 :
:
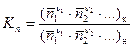 .
.
По этому выражению видно, что чем меньше 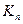 , тем в равновесной смеси присутствует больше начальных веществ, и наоборот, чем
, тем в равновесной смеси присутствует больше начальных веществ, и наоборот, чем 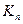 больше, тем больше конечных веществ. Очевидно, что полной реакции соответствовало бы бесконечно большое значение константы равновесия
больше, тем больше конечных веществ. Очевидно, что полной реакции соответствовало бы бесконечно большое значение константы равновесия 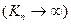 .
.
Определение равновесного состава реагирующей смеси. Константа равновесия может быть подсчитана, если известен равновесный состав смеси. Но можно решить и обратную задачу - определить равновесный состав смеси, исходя из известного значения константы равновесия.
Допустим, что значение константы равновесия задано, Тогда задача определения равновесного состава реакции решается в следующем порядке. Воспользуемся соотношением между константами равновесия 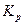 и
и 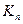 :
:
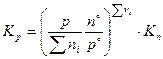 .
.
Выберем масштабы отнесения давления и количества вещества. От выбора масштабов отнесения зависит, в каких единицах следует подставлять в формулы 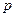 и
и 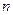 . Так как за единицу количества вещества мы принимаем киломоль, то
. Так как за единицу количества вещества мы принимаем киломоль, то 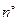 = 1 кмоль. В термодинамике и в химии принимают
= 1 кмоль. В термодинамике и в химии принимают 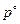 = 1 физ. атм., т.е. давление, соответствующее нормальным и стандартным условиям. Следовательно, значения
= 1 физ. атм., т.е. давление, соответствующее нормальным и стандартным условиям. Следовательно, значения 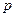 и
и 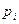 нужно подставлять также в физ. атм. Однако можно выбрать
нужно подставлять также в физ. атм. Однако можно выбрать 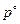 и в других единицах (1 бар, 1 Па, 1 кПа и т.п.), но соблюдать безразмерность
и в других единицах (1 бар, 1 Па, 1 кПа и т.п.), но соблюдать безразмерность  .
.
Итак, с учетом масштабов отнесения
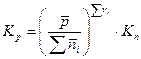 . (А)
. (А)
Поскольку масштабы единичные, то 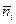 численно равны
численно равны 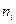 .
.
Выразим 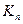 через равновесный состав:
через равновесный состав: 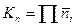 , а равновесный состав - через меру реакции. Мера реакции равна изменению числа кмоль, деленному на стехиометрический коэффициент:
, а равновесный состав - через меру реакции. Мера реакции равна изменению числа кмоль, деленному на стехиометрический коэффициент:
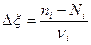 . (6)
. (6)
В этом уравнении 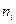 - число кмоль i -того вещества в равновесной смеси,
- число кмоль i -того вещества в равновесной смеси, 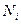 - число кмоль этого вещества перед началом реакции. Величина
- число кмоль этого вещества перед началом реакции. Величина  , выражаемая через равновесный состав, характеризует степень полноты (завершенности) реакции.
, выражаемая через равновесный состав, характеризует степень полноты (завершенности) реакции.
Из уравнения (6) выразим равновесный состав реакции:
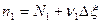 ,
,
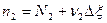 ,
,
........ (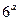 )
)
........
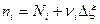 ,
,
........
и подставим его в 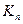 :
:
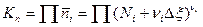 . (7)
. (7)
Далее подставим выражение (7) в уравнение (А):
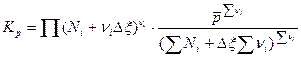 . (8)
. (8)
Здесь 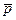 - безразмерное давление смеси,
- безразмерное давление смеси, 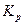 - заданное значение константы равновесия. Уравнение (8) решается относительно величины Dx способом последовательных приближений. По полученному значению меры реакции определим равновесный состав реагирующей смеси, пользуясь уравнениями (
- заданное значение константы равновесия. Уравнение (8) решается относительно величины Dx способом последовательных приближений. По полученному значению меры реакции определим равновесный состав реагирующей смеси, пользуясь уравнениями (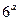 ).
).
Химическое сродство.
При исследовании химической реакции в первую очередь необходимо выяснить, способны ли данные вещества в данных условиях вступать в реакцию, а если способны, то в каком направлении пойдет реакция - в прямом или в обратном. Для решения этого вопроса необходимо выработать соответствующие термодинамические соотношения.
Способность различных веществ вступать в химическое взаимодействие называется химическим сродством. Условиями, в которых исследуется сродство, являются, во-первых, температура и давление, при которых происходит реакция, и во-вторых, исходные и равновесные концентрации или парциальные давления. Для того, чтобы связать химическое сродство с условиями протекания реакции, необходимо это сродство выразить количественно, т.е. иметь меру химического сродства.
Критерий, который мог бы служить мерой химического сродства, был найден не сразу. В начале было выдвинуто насколько неудачных предложений. Первым правильную точку зрения по этому вопросу высказал Дж.В. Гиббс (1878), который предложил использовать в качестве меры химического сродства максимальную работу, т.е. ту работу, которую можно получить за счет данной реакции при ее термодинамически обратимом проведении в данных условиях. Позже нидерландский ученый Я. Вант-Гофф (1885) независимо от Гиббса выдвинул такое же предложение.
В разделе «Характеристические функции» было выяснено, что максимальная работа выражается через изменение соответствующей характеристической функции. В применении к реакциям 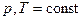 это означает, что мерой химического сродства является изменение энергии Гиббса
это означает, что мерой химического сродства является изменение энергии Гиббса 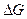 , в применении к реакциям
, в применении к реакциям 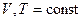 - изменение энергии Гельмгольца
- изменение энергии Гельмгольца  .
.
Допустим, что взяты вещества В1 и В2 и при взаимодействии между ними образуются вещества В3 и В4:
n1В1 + n2В2 = n3В3 + n4В4 .
Мы знаем, что в сложной системе процесс перераспределения масс может идти только в сторону уменьшения характеристической функции. В данном случае перераспределением масс является превращение веществ В1 и В2 в вещества В3 и В4 - прямая реакция. Следовательно, если при некоторых условиях при переходе реакции из химически неравновесного состояния в равновесное окажется, что 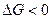 или
или 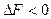 , то это будетозначать, что реакция пойдет в прямом направлении. При этом значения
, то это будетозначать, что реакция пойдет в прямом направлении. При этом значения 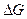 и
и  будут выражать химическое сродство между веществами В1 и В2.
будут выражать химическое сродство между веществами В1 и В2.
Если же условия протекания реакции изменятся так, что характеристическая функция будет увеличиваться ( ,
, 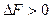 ), то это будет означать, что реакци пойдет в обратном направлении, т.е. с образованием веществ В1 и В2, а значения
), то это будет означать, что реакци пойдет в обратном направлении, т.е. с образованием веществ В1 и В2, а значения 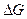 и
и  будут тогда выражать химическое сродство между веществами В3 и В4.
будут тогда выражать химическое сродство между веществами В3 и В4.
Мы видим, что величины 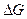 и
и  удовлетворяют тем требованиям, которые могут быть предъявлены к величине, характеризующей химическое сродство:
удовлетворяют тем требованиям, которые могут быть предъявлены к величине, характеризующей химическое сродство:
1) они не зависят от пути, по которому протекает реакция, а зависят только от свойств реагентов и от того их состояния, в котором реакция начинается и оканчивается;
2) знаки 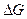 и
и  определяют направление, в котором протекает реакция.
определяют направление, в котором протекает реакция.
Теперь мы можем сформулировать определение понятия «химическое сродство»:
Химическое сродство измеряется значением изменения характеристической функции при переходе реакции из неравновесного состояния в равновесное; при этом знак изменения характеристической функции указывает направление реакции.
Уравнение изотермы реакции. Свяжем химическое сродство с условиями протекания реакции. Уравнение
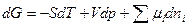 , кДж
, кДж
представим в конечной форме:
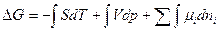 .
.
При 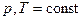
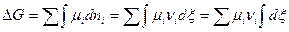
или
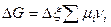 , кДж.
, кДж.
Отнесем это уравнение к мере реакции и получим
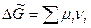 , кДж/кмоль,
, кДж/кмоль,
но попрежнему откажемся от обозначения 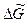 и будем записывать без волны:
и будем записывать без волны:
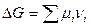 , кДж/кмоль (1)
, кДж/кмоль (1)
Исходным состоянием реакции будем считать некоторое промежуточное состояние, когда в смеси присутствуют не только начальные вещества, но и конечные, а равновесие еще не наступило. Обозначим через 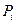 парциальные давления составляющих реакции в неравновесной смеси, а через
парциальные давления составляющих реакции в неравновесной смеси, а через 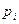 - в равновесной. Используем полученное выше выражение (6) для химического потенциала i -той составляющей:
- в равновесной. Используем полученное выше выражение (6) для химического потенциала i -той составляющей:
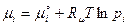 ,
,
подставив его в уравнение (1). Тогда для неравновесной смеси
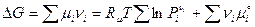 (2)
(2)
и для равновесной
 . (3)
. (3)
Из последнего уравнения получим
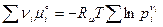 . (4)
. (4)
Как было выяснено выше, величина 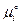 зависит только от температуры, поэтому в выражениях (2) и (3) она одна и та же. Поэтому подставив (4) в (2), будем иметь
зависит только от температуры, поэтому в выражениях (2) и (3) она одна и та же. Поэтому подставив (4) в (2), будем иметь
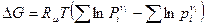
или
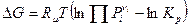 . (5)
. (5)
Полученное уравнение называется уравнением изотермы реакции. Аналогично можно получитьуравнение изотермы для условий 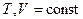 :
:
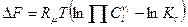 . (6)
. (6)
Здесь 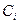 - концентрации реагирующих веществ в неравновесной смеси, а
- концентрации реагирующих веществ в неравновесной смеси, а  - константа равновесия.
- константа равновесия.
Замечание. Можно выразить 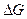 через концентрации и
через концентрации и  , а
, а  через парциальные давления и
через парциальные давления и 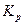 , но более употребительны формул, полученные выше.
, но более употребительны формул, полученные выше.
Уравнения изотермы реакции связывают химическое сродство с условиями протекания реакции, а именно, по уравнениям (5) и (6) видно, что химическое сродство изменяется в зависимости от исходных (произвольных) и равновесных (определяющих значение 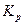 ) парциальных давлений или концентраций и от температуры. По этим уравнениям можно определить возможное направление протекания реакции в данных условиях.
) парциальных давлений или концентраций и от температуры. По этим уравнениям можно определить возможное направление протекания реакции в данных условиях.
Пример. Для реакции
СО + Н2О = СО2 + Н2
При температуре Т = 1500 К константа равновесия 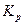 = 0,3 (р, бар). Определить, в каком направлении реакция
= 0,3 (р, бар). Определить, в каком направлении реакция 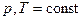 будет протекать при следующих значениях парциальных давлений веществ в неравновесной смеси: а)
будет протекать при следующих значениях парциальных давлений веществ в неравновесной смеси: а)  бар,
бар, 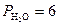 бар,
бар, 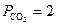 бар,
бар, 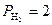 бар и б)
бар и б) 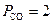 бар,
бар, 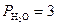 бар,
бар,  бар,
бар, 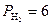 бар.
бар.
Решение. Составим уравнение изотермы реакции:
 .
.
Случай а) 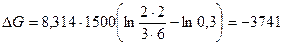 кДж/кмоль, т.е.
кДж/кмоль, т.е. 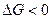 .
.
Выражение в скобке показывает: чтобы реакция пришла к равновесию (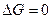 ) при заданных парциальных давлениях равновесной смеси (т.е. при заданном значении
) при заданных парциальных давлениях равновесной смеси (т.е. при заданном значении 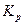 ), нужно, чтобы логарифм со знаком плюс (слева) увеличивался, т.е. чтобы неравновесные парциальные давления СО2 и Н2 увеличивались, а СО и Н2О - уменьшались. Это соответствует протеканию реакции в сторону образования СО2 и Н2 (вправо), следовательно, значение
), нужно, чтобы логарифм со знаком плюс (слева) увеличивался, т.е. чтобы неравновесные парциальные давления СО2 и Н2 увеличивались, а СО и Н2О - уменьшались. Это соответствует протеканию реакции в сторону образования СО2 и Н2 (вправо), следовательно, значение 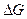 выражает сродство между СО и Н2О.
выражает сродство между СО и Н2О.
Случай б) 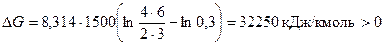 .
.
Чтобы в этом случае реакция пришла к равновесию, нужно, чтобы неравновесные парциальные давления СО2 и Н2 уменьшались. Это соответствует протеканию реакции в сторону образования СО и Н2О (влево), следовательно, значение 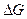 выражает сродство между СО2 и Н2.
выражает сродство между СО2 и Н2.
Придерживаясь принятого здесь правила знаков стехиометрических коэффициентов, можно просто утверждать: если 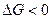 , то реакция пойдет слева направо; если
, то реакция пойдет слева направо; если  - то справа налево. Но при этом необходимо уметь объяснять, из чего видно, что это именно так.
- то справа налево. Но при этом необходимо уметь объяснять, из чего видно, что это именно так.
Нормальное химическое сродство. По уравнению изотермы реакции видно, что химическое сродство для одной и той же реакции при одной и той же температуре имеет различные значения в зависимости от исходных (неравновесных) парциальных давлений или концентраций. Поэтому для определенности вводится понятие нормального химического сродства.
Нормальным химическим сродством называется значение изменения энергии Гиббса или энергии Гельмгольца, получаемое при заданной температуре и при условии, что исходные парциальные давления (в первом случае) или концентрации (во втором случае) всех составляющих реакции имеют единичные значения.
В этом случае слагаемые 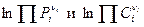 в уравнениях (5) и (6) становятся равными нулю, и мы получаем выражения для нормального химического сродства:
в уравнениях (5) и (6) становятся равными нулю, и мы получаем выражения для нормального химического сродства:
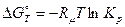 и
и 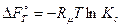 . (7)
. (7)
Индекс «Т» соответствует температуре, при которой происходит реакция.
Если значение нормального химического сродства известно, то можно вычислить значение константы равновесия при температуре Т:
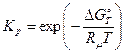 и
и 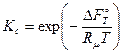 . (Х)
. (Х)
Стандарное химическое сродство образования. Химическое сродство некоторой химической реакции (Б) удобно выражать через значения химического сродства реакций образования веществ, участвующих в реакции (Б). Химическое сродство реакций образования (или просто химическое сродство образования) для различных веществ сводят в таблицы, для чего его определяют при стандартных условиях (р ° = 1 атм, Т 0 = 298,15 К) и называют стандартным химическим сродством образования.
Стандартным химическим сродством образования вещества называется нормальное сродство реакции образования этого вещества из элементов при стандартных условиях. В зависимости от вида реакции - 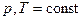 или
или 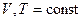 - стандартное химическое сродство образования обозначается
- стандартное химическое сродство образования обозначается 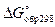 (стандартная энергия Гиббса) или
(стандартная энергия Гиббса) или 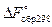 (стандартная энергия Гельмгольца).
(стандартная энергия Гельмгольца).
В термодинамических таблицах приведены значения стандартной энергии Гиббса 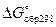 . Значения
. Значения 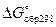 для элементов приняты равными нулю.
для элементов приняты равными нулю.
Значения 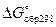 получают экспериментально, проводя соответствующую реакцию в лабораторных условиях. Наиболее точно они определяются по ЭДС гальванического элемента в связи с тем, что в гальваническом элементе можно проводить химическую реакцию практически обратимо, т.е. получать максимальное значение полезной работы
получают экспериментально, проводя соответствующую реакцию в лабораторных условиях. Наиболее точно они определяются по ЭДС гальванического элемента в связи с тем, что в гальваническом элементе можно проводить химическую реакцию практически обратимо, т.е. получать максимальное значение полезной работы  .
.
Максимальная полезная работа связана с электродвижущей силой гальванического элемента уравнением:
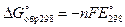 ,
,
где n - число молей электронов, приходящееся на один моль прореагировавшего вещества и протекших через внешнюю цепь при стандартных условиях; F = = 9,65×107 Кл/кмоль - постоянная Фарадея, 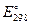 - электродвижущая сила. Измеряя ЭДС, получают значение энергии Гиббса.
- электродвижущая сила. Измеряя ЭДС, получают значение энергии Гиббса.
Замечания. 1) ЭДС представляет собой максимальное значение напряжения гальванического элемента, соответствующее обратимому протеканию химической реакции.
2) Получаемое значение 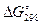 относится к тому веществу, которое является продуктом реакции в данном гальваническом элементе с определенным (щелочным или кислым) электролитом. Например, в воздушно-цинковом элементе со щелочным электролитом (NaOH) протекает реакция Zn + ½ O2 + 2NaOH = Na2ZnO2 + H2O. Это реакция образования Na2ZnO2, к нему и относится
относится к тому веществу, которое является продуктом реакции в данном гальваническом элементе с определенным (щелочным или кислым) электролитом. Например, в воздушно-цинковом элементе со щелочным электролитом (NaOH) протекает реакция Zn + ½ O2 + 2NaOH = Na2ZnO2 + H2O. Это реакция образования Na2ZnO2, к нему и относится 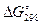 .
.
Стандартное химическое сродство 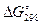 реакции между различными веществами подсчитывается по значениям
реакции между различными веществами подсчитывается по значениям 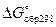 по следующей формуле:
по следующей формуле:
 . (А)
. (А)
Эта формула написана по аналогии с формулой для стандартного значения теплового эффекта [формула (8) в разделе «Закон Гесса»], так как величина G, как и Н, является функцией состояния, т.е. ее изменение не зависит от пути проведения реакции.
Пример. Константа равновесия реакции
Н2 +I2 = 2HI
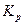 = 50 при температуре 717 К. Определить нормальное химическое сродство при этой температуре и направление реакции.
= 50 при температуре 717 К. Определить нормальное химическое сродство при этой температуре и направление реакции.
Решение. По формуле (7)
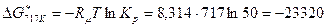 кДж/кмоль.
кДж/кмоль.
Реакция протекает в сторону образования HI.
Зависимость химического сродства от температуры.
Как было выяснено в разделе «Сложные системы», уравнения Гиббса-Гельмгольца имеют вид:
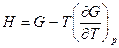 и
и 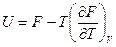 .
.
Будем рассматривать условия 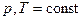 и перепишем первое уравнение иначе:
и перепишем первое уравнение иначе:
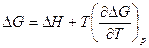 .
.
Поскольку 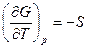 , то
, то
 . (В)
. (В)
Здесь 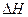 - изобарный тепловой эффект и
- изобарный тепловой эффект и 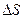 - изменение энтропии в реакции. Чтобы получить зависимость
- изменение энтропии в реакции. Чтобы получить зависимость 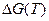 , нужно воспользоваться выражениями
, нужно воспользоваться выражениями 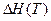 и
и 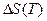 . Зависимость теплового эффекта от температуры
. Зависимость теплового эффекта от температуры 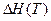 была получена раньше при условии. что теплоемкости реагирующих веществ выражаются многочленами:
была получена раньше при условии. что теплоемкости реагирующих веществ выражаются многочленами:
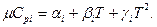
Теперь получим выражение для изменения энтропии в зависимости от температуры. Для этого нужно проинтегрировать выражение
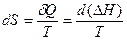 .
.
По уравнению Кирхгофа
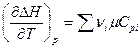 ,
,
откуда для реагирующей смеси 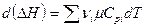 .
.
Учитывая принятую зависимость теплоемкости от температуры, получим:
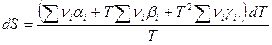 .
.
Проинтегрируем это выражение в пределах от стандартного состояния до состояния. соответствующего некоторой температуре Т и получим:
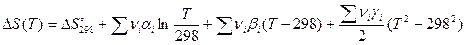 . (С)
. (С)
Величина  , входящая в
, входящая в 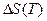 , определяется по табличным данным. Выражение
, определяется по табличным данным. Выражение 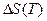 и полученное ранее выражение
и полученное ранее выражение 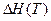 (см. раздел «закон Кирхгофа»)
(см. раздел «закон Кирхгофа»)
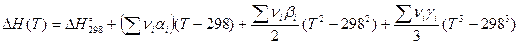
подставим в (В). В результате будем иметь:
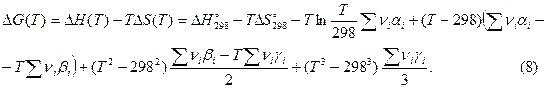
Зависимость константы равновесия от температуры.
Уравнения изобары и изохоры реакции. Уравнения изобары и изохоры реакции представляют собой дифференциальные уравнения, выражающие связь между константой равновесия, тепловым эффектом реакции и температурой.
Получим сначала уравнение изобары реакции. Для этого используем уравнение Гиббса-Гельмгольца и уравнение изотермы реакции:
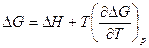 ;
;
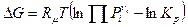 .
.
Из закона действующих масс следует, что константа равновесия зависит от температуры. Продифференцировав второе уравнение по температуре, будем иметь:
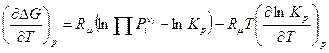 .
.
Подставим этот результат в уравнение Гиббса-Гельмгольца и получим:
 .
.
С учетом того, что
Date: 2015-09-18; view: 727; Нарушение авторских прав