Квантовая вероятность

⇐ ПредыдущаяСтр 170 из 239Следующая ⇒

Как нам уже известно, Эйнштейн не разделял выводов квантовых физиков о вероятностной структуре процессов, идущих во Вселенной. Эйнштейн и Планк, до конца своих жизней остались верны принципам полной математической предсказуемости процессов в Объективной реальности[67]. Об этом пишет Б.Грин (выделено нами):

«Ушли те дни, когда Вселенная представлялась работавшим как часы механизмом, объекты которого, приведённые в движение в какой-то момент в прошлом, покорно следовали к неизбежному, единственным образом определяемому пункту назначения. Согласно квантовой механике Вселенная развивается в соответствии со строгими и точными математическими законами, но эти законы определяют только вероятность того, что может наступить то или иное конкретное будущее, и ничего не говорят о том, какое будущее наступит в действительности.

Многие сочтут этот вывод обескураживающим или даже совершенно неприемлемым. Одним из таких людей был Эйнштейн. В одном из наиболее известных в истории физики высказываний он предостерегал сторонников квантовой механики: «Бог не играет в кости со Вселенной» [68]. Он считал, что вероятность появляется в фундаментальной физике по той же причине, по которой она появляется в игре в рулетку: вследствие существенной неполноты нашего знания. С точки зрения Эйнштейна, во Вселенной нет места для будущего, точное содержание которого включает элементы вероятности. Физики должны предсказывать, как будет развиваться Вселенная, а не определять вероятность того, что события могут пойти каким-то путём. Но эксперимент за экспериментом (некоторые из наиболее впечатляющих были выполнены уже после его смерти) убедительно подтверждали, что Эйнштейн был не прав. Как заметил однажды по этому поводу британский физик‑теоретик Стивен Хокинг. «Заблуждался Эйнштейн, а не квантовая теория».

Итак, признав, что Эйнштейн заблуждался, квантовые физики всё-таки взяли на вооружение не что-то свежее, а Общую теорию относительности и приспособили её к квантовому миру. К тому же, если рассмотреть знаменитое высказывание Эйнштейна «Он [Бог] не бросает кости» вне контекста того, как это понимал сам Эйнштейн[69] — он оказался прав: Бог действительно не следует «воле случая», но по-крупному. Он задал наперёд не однозначный результат развития, а Матрицу (Меру) возможных состояний. В общем-то к этому выводу и подводили учёных их же опыты на уровне квантового мира весь период развития науки после «эпохи Эйнштейна». Однако, если А.Эйнштейн вообще не давал никакой свободы развития интеллектуальным элементам Вселенной, то квантовые физики своими выводами создали «научную» почву, на базе которой возникла очередная научно-атеистическая безмерная эсхатологическая иллюзия (к тому же весьма опасная своей научно обоснованной вседозволенностью)[70]. Общая теория относительности с её космологической доктриной[71] объединила физиков «эпохи Эйнштейна» и квантовых физиков конца XX – начала XXI вв.

Рассмотрим как квантовые физики разрушали старые планковско-эйнштейновские представления о поведении Объективной реальности[72]. Начнём с некоторых широко известных вещей. Известная всем волновая теория света началась с опытов, поставленных членом Лондонского королевского общества Томасом Юнгом. В 1801 г. он объяснил явление интерференции света, дал интерпретацию «колец Ньютона». История развития исследований в области волновой теории света хорошо описана у Б.Грина:

«Представим, что вместо световых волн мы рассматриваем волны на поверхности воды. Это не повлияет на результат, но такие волны более наглядны. Когда волна сталкивается с преградой, то, как показано на рисунке ниже, от каждой щели распространяется новая волна, похожая на ту, которая возникает, если бросить камешек в пруд. (Это легко проверить, используя картонный лист с двумя прорезями, помещенный в чашку с водой.) Когда волны, идущие от каждой щели, накладываются друг на друга, происходит интересное явление. При наложении двух волновых максимумов высота волны в соответствующей точке увеличивается — она равна сумме высот максимумов двух наложившихся волн. Аналогично, при наложении двух минимумов глубина впадины, образовавшейся в этой точке, также увеличивается. Наконец, если максимум одной волны совпадает с минимумом другой, они взаимно гасят друг друга. (На этом основана конструкция фантастических шумопоглощающих наушников — они определяют форму пришедшей звуковой волны и генерируют другую, форма которой в точности «противоположна» первой, что приводит к подавлению нежелательного шума.) Между этими крайними случаями — максимум с максимумом, минимум с минимумом и максимум с минимумом — расположен весь спектр частичного усиления и частичного ослабления. Если вы с компанией друзей сядете в небольшие лодки, выстроите их в линию параллельно преграде и каждый из вас будет сообщать, насколько сильно его качает при прохождении волны, результат будет похож на тот, который изображен на рисунке.

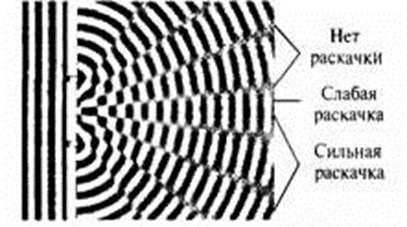
Круговые волны на воде, идущие от каждой щели, накладываются одна на другую; это приводит к тому, что в одних местах результирующая волна будет усиливаться, а в других ослабляться.

Точки с сильной качкой будут расположены там, где накладываются максимумы (или минимумы) волн, приходящих от разных щелей. Участки с минимальной качкой или полным ее отсутствием окажутся там, где максимумы волны, идущей от одной щели, будут совпадать с минимумами волны, идущей от другой щели».

Юнг провёл подобный опыт, но не с водой, а со светом, то есть с электромагнитным полем.

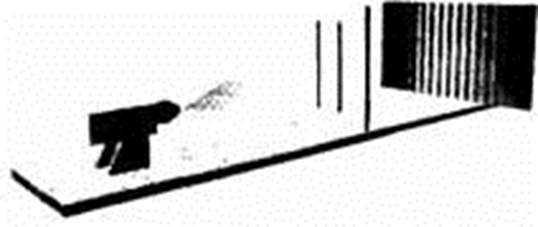
«Самые яркие участки на рисунке представляют области, в которых максимумы (или минимумы) световых волн, пришедших от разных щелей, совпадают. Тёмными являются участки, в которых максимум одной волны складывается с минимумом другой, приводя к взаимному погашению. Такая последовательность светлых и тёмных полос известна под названием интерференционной картины.

Подобный эксперимент был выполнен Юнгом, и его результат совпал с картиной, показанной на предыдущем рисунке, тем самым подтвердив волновую природу света. Ньютоновская теория корпускулярной природы света была отвергнута (хотя потребовалось некоторое время, прежде чем все физики согласились с этим). Доминирующая волновая теория света впоследствии получила надёжное математическое обоснование в теории Максвелла».

После этого Эйнштейн вместе с Планком, принявшие волновую теорию света, внесли в неё новую «корпускулярную составляющую», введя понятие фотона — минимального кванта света, частиц света. Опять возникла неопределённость: свет (электромагнитное излучение) — это волна или частица, или и то и другое сразу? Фотоны оказались частицами, обладающими волновыми свойствами. Об этом пишет Б.Грин (выделено нами):

«Эксперименты показали, что частицы света Эйнштейна довольно существенно отличаются от частиц Ньютона. Каким-то образом фотоны — хотя они и являются частицами — обладают также и волновыми свойствами света. Тот факт, что энергия этих частиц определяется параметром, используемым для описания волн, т. е. частотой, является первым признаком того, что это странное объединение действительно имеет место. Однако фотоэффект и эксперимент с двумя щелями ещё более озадачивают нас. Фотоэффект показывает, что свет имеет свойства частиц[73]. Эксперимент с двумя щелями демонстрирует, что свет также проявляет интерференционные свойства, характерные для волн. Вместе они показывают, что свет обладает и волновыми, и корпускулярными свойствами. Микромир требует, чтобы при попытке его описания мы отказались от наших интуитивных представлений [74] о том, что любой объект представляет собой либо волну, либо частицу, и чтобы мы учитывали возможность того, что он может быть волной и частицей одновременно. Это один из тех случаев, когда высказывание Фейнмана о том, что «никто не понимает квантовую механику», является особенно актуальным. Мы можем произносить слова типа «корпускулярно‑волновой дуализм». Мы можем преобразовать эти слова в математическую модель, которая воспроизведёт экспериментальные данные с поразительной точностью. Но добиться глубокого, интуитивного понимания[75] этой ошеломляющей особенности микромира необычайно трудно.

В 1923 г. молодой французский аристократ, князь Луи де Бройль, добавил новый элемент в квантовую мешанину, который вскоре помог разработать математический аппарат современной квантовой механики и принёс ему Нобелевскую премию 1929 г. по физике. Вдохновлённый цепочкой рассуждений, восходящих к специальной теории относительности Эйнштейна, де Бройль предположил, что корпускулярно‑волновой дуализм применим не только к свету, но и к веществу. Его аргументы, если опустить детали, состоят в том, что эйнштейновское уравнение Е = mс2 связывает массу с энергией; но с другой стороны, Планк и Эйнштейн связали энергию с частотой волн. Объединяя эти два факта, можно прийти к выводу, что масса должна иметь и волновое воплощение».

Прервём цитирование, чтобы ещё раз обратить внимание на неразрывную связь массы вещества (частицы) с энергией. Ранее было высказано, что масса представляет собой «замороженную» энергию, что свидетельствует о единой сущности энергии и вещества, которая называется предельно обобщённым понятием «материя». В то же время волновая характеристика («частота волны»), зависимость от которой «порций энергии» физики стали наблюдать с момента введения Планком понятия квант — стала проявляться всё отчётливее по мере проведения дальнейших исследований. Про них пишет Б.Грин:

«После долгих размышлений де Бройль предположил, что так же, как свет является волновым явлением, которое, как показывает квантовая теория, имеет равно обоснованное корпускулярное описание, так и электрон, который мы обычно считаем частицей, может иметь равно обоснованное волновое описание. Эйнштейн сразу принял идею де Бройля, поскольку она была естественным развитием его собственного вклада в теорию относительности и теорию фотонов. Однако без экспериментального подтверждения всё равно нельзя было обойтись. Такое подтверждение было вскоре получено в работах Клинтона Дэвиссона и Лестера Джермера.

В середине 1920‑х гг. Дэвиссон и Джермер, физики‑экспериментаторы из лаборатории телефонной компании Белл, исследовали рассеяние электронов на атомах никеля. Для нас их исследования интересны тем, что кристаллы никеля в этих экспериментах действовали во многом подобно щелям в опыте, описанном и проиллюстрированном в предыдущем разделе [76]. На самом деле можно считать эксперименты практически идентичными, за исключением того, что вместо луча света использовался пучок электронов. Дэвиссон и Джермер исследовали электроны, пропуская их через две щели, сквозь которые они могли попадать на фосфоресцирующий экран, оставляя на нём светящиеся точки, точно так же, как на экране телевизора, и обнаружили поразительное явление. На экране появлялась картина, очень похожая на ту, которая показана на рисунке выше. Эксперимент, таким образом, показывал, что электроны создают интерференционную картину, которая является неоспоримым признаком волн».

Опять прервём цитирование чтобы ещё раз обратить внимание на выявленный эффект: «твёрдые» микрочастицы частицы вещества (в данном случае электроны) ведут себя, проявляя признаки волн. Иными словами их физическая траектория в процессе опыта является некой «волновой функцией» движения частицы в пространстве с присущей волнам интерференционной картиной. Знакомые физикам пространственно-временные характеристики траекторий микрочастиц оказались не единственными параметрами, задающими «координаты» движения и места дислокации частиц на экране. Последнее говорит о том, что пространственные и временные ориентиры не являются всеми необходимыми данными для описания динамического поведения и дислокации относительного «покоя» чего-то материального. Для этого нужно точно знать всю «волновую функцию», или полный набор дополнительных (к пространственно-верменным) характеристик, определяющих состояние материальной субстанции. Одной из таких характеристик является частота излучения (длина волны). То есть, есть нечто, объединяющее все частные характеристики, с помощью чего можно описать полную картину “материализации” волновой функции (на опыте Дэвиссона и Джермера картина представлена окончательным расположением электронов на экране).

«В тёмных точках на фосфоресцирующем экране электроны каким-то образом «нейтрализовали» друг друга, совсем как при наложении гребней и впадин волн, распространяющихся по поверхности волны. Даже если «сжать» пучок электронов до такой степени, что один электрон будет излучаться один раз в десять секунд, отдельные электроны по-прежнему будут образовывать яркие и темные полосы — по одному пятну за один раз. Как и фотоны, отдельные электроны каким-то образом «интерферируют» сами с собой в том смысле, что с течением времени отдельные электроны воссоздают интерференционную картину, которая ассоциируется с волнами. Мы с неизбежностью вынуждены заключить, что наряду с более привычным описанием на языке частиц каждый электрон проявляет и волновые свойства.

Описанные выше эксперименты относятся к электронам, однако схожие эксперименты позволяют сделать вывод о том, что всё вещество имеет волновые свойства.

Но как это согласуется с нашим повседневным опытом, говорящим о том, что вещество — это нечто сплошное и твёрдое, и уж никак не похожее на волны? Де Бройль предложил формулу для длины волны частиц вещества [77], которая показывает, что длина волны пропорциональна постоянной Планка h. (Если говорить более точно, длина волны определяется как частное от деления на импульс материального тела.) Поскольку величина очень мала, длина волны также является очень малой по обычным масштабам. Именно по этой причине волновые характеристики материи становятся наблюдаемыми только в высокоточных микроскопических исследованиях. Точно так же, как большая величина скорости света «с» скрывает истинные свойства пространства и времени, малость маскирует волновые свойства материи в окружающем нас мире.

Явление интерференции, открытое Дэвиссоном и Джермером, реально продемонстрировало, что электроны подобны волнам. Но при этом возникает естественный вопрос: волнам чего? Одно из первых предположений на эту тему, сделанное австрийским физиком Эрвином Шрёдингером, заключалось в том, что эти волны представляют собой «размазанные» электроны. Это предположение отчасти улавливало «сущность» электронной волны, но было слишком неточным. Когда вы размазываете что-нибудь, часть его находится здесь, а другая часть в другом месте. Однако никому и никогда не приходилось иметь дело с половиной или с третью, или с иной частью электрона. Это усложняло понимание того, что представляет собой размазанный электрон. В 1926 г. немецкий физик Макс Борн существенно уточнил предложенную Шрёдингером интерпретацию электронной волны, и именно этой интерпретацией, усиленной Бором и его коллегами, мы пользуемся и сегодня. Утверждение Борна касается одного из самых странных свойств квантовой теории, тем не менее, оно подтверждается огромным количеством экспериментальных данных. Согласно этому утверждению электронная волна должна интерпретироваться с точки зрения вероятности. В тех областях, где амплитуда (или, точнее, квадрат амплитуды) волны больше, обнаружение электрона более вероятно; в местах, где амплитуда мала, вероятность обнаружить электрон меньше. Пример показан на рисунке».

Волна, ассоциированная с электроном, имеет наибольшую амплитуду в тех местах, где обнаружение электрона наиболее вероятно; амплитуда волны убывает по мере уменьшения вероятности обнаружения электрона».

Что это, как не матрица (мера) возможных положений электрона на поверхности экрана — в основе которой лежит непрерывный волновой процесс[78]? Эта матрица возможных положений чисто гипотетически должна описываться с помощью определённого количества параметров (амплитуды, частоты волны, координат и т.п.) — являющихся величинами, определяющими всю матрицу (меру), или частными мерами, с помощью которых можно описать всю меру (если, конечно все их знать). Но вообразить у себя в психике матрицу возможных состояний можно и без построения абстрактной модели, выведенной на базе математического описания всех частных мер. Матрицу возможных состояний можно вообразить на основе ощущения этих частных мер. Это легко увидеть, глядя на вышерасположенный рисунок — вероятностную матрицу расположения электрона на экране. Эта матрица, перенесённая на экран опытным путём, имеет чёткий образ. Глядя на этот образ, можно получить полную информационную “картинку” о матрице возможных положений электрона без абстрактных расчётов и параметров. Но мы знаем, что “картинка”, изображённая на рисунке, получена опытным путём [79]. Иными словами, образ чего-то можно создать на бумаге, представить на экране, в пространстве (либо в голове) с помощью его абстрактного описания либо с помощью опыта — достаточно лишь взглянуть на полученную опытную “картинку”. В принципе с этого момента (1926 год)[80] у учёных были все основания высказаться в пользу неразрывного триединства Вселенной материя-информация-мhра. Но, как это часто бывает, базовые мировоззренческие открытия делают не физики, а «лирики»[81].

Следующий за вышеприведённым рисунком текст книги Б.Грина — яркое свидетельство того, что «западный учёный ум» не может себе вообразить Вероятностную Предопределённость как основной закон “теории поля” Объективной реальности — Вселенной[82]:

«Какое отношение имеет вероятность к формулировке фундаментальных законов физики? Мы привыкли к тому, что вероятность присуща лошадиным бегам, подбрасыванию монеты или игре в рулетку, но в этих случаях она просто является отражением неполноты нашего знания. Если мы точно знаем скорость колеса рулетки, вес и твёрдость шарика, который бегает по нему, положение и скорость шарика в тот момент, когда он падает на колесо, свойства материала ячеек и т. п., и если мы используем для наших вычислений достаточно мощные компьютеры, мы можем, в соответствии с законами классической физики, совершенно точно предсказать, где остановится шарик. В казино полагаются на неспособность игрока получить всю эту информацию и провести необходимые вычисления перед тем, как сделать ставку. Однако ясно, что вероятность, с которой приходится сталкиваться во время игры в рулетку, не отражает никаких фундаментальных свойств Вселенной. Напротив, квантовая механика вводит понятие вероятности в устройство мироздания на гораздо более глубоком уровне. Согласно утверждению Борна, подкрепленному собранными более чем за полвека экспериментальными данными, наличие у материи волновых свойств подразумевает, что фундаментальное описание материи должно иметь вероятностный характер. Закон де Бройля показывает, что для макроскопических объектов, таких как кофейная чашка или рулеточное колесо, волновые свойства являются практически ненаблюдаемыми, и в обычных ситуациях связанная с ними квантово‑механическая вероятность может полностью игнорироваться. Но этот же закон говорит, что на микроскопическом уровне мы, в лучшем случае, можем указать только вероятность того, что электрон будет обнаружен в любом заданном месте».

«Вероятность» в смысле выпадения чего-то определённого в результате подбрасывания монеты и игры в рулетку и даже «вероятность» в смысле точного математического «фундаментального описания материи» — это далеко не матрица возможных состояний материи. Тем более это не Вероятностная Предопределённость. Даже в случае «точного» математического «фундаментального описания материи» (т.е. законов Вселенной, как следует из контекста рассуждений автора книги) неизбежны ошибки, связанные с неадекватностью ограниченного математического аппарата, ограниченностью интеллекта учёных и возможностей опытного подтверждения — огромному количеству параметров “настройки” Вселенной (из которых складывается вся Вероятностная Предопределённость).

В результате теоретического выведения законов такой математической вероятности, всегда будет оставаться место для неопределённости (как на микроскопическом уровне, так и на макроскопическом), вызванной, как правило, неучтёнными при расчетах, но объективно существующими параметрами “настройки” Вселенной. И, как бы западные учёные не “рыли землю” в поисках всё меньших частиц, они не учитывают в своей деятельности ряд самых важных и первоприоритетных параметров настройки Вселенной (о них разговор пойдёт далее). Иными словами, наука уже давно пытается через математику и опыты «ухватить Бога за бороду» для выявления механизма функционирования Вселенной («отразить фундаментальные свойства Вселенной»), отрицая Бога-Вседержителя или не веря Ему.

Следующая цитата из книги Б.Грина подтверждает это. Мы видим, что может получиться, если переносить изведанные наукой вероятностные законы поведения микромира на фундаментальные свойства всей Вселенной:

«Допустим, что электронные волны [83] обладают теми же свойствами, что и все другие волны, например, они могут сталкиваться с препятствиями и образовывать вторичные волны. Однако в рамках вероятностного описания из этого не следует, что сам электрон распадается на части. Это означает лишь, что имеются области, в которых электрон может появиться с ненулевой вероятностью. На практике это означает, что если мы будем снова и снова повторять совершенно одинаковым образом какой-либо эксперимент с электроном, касающийся, например, измерения его положения, мы не будем всегда получать одинаковый результат. Повторяющиеся эксперименты дадут набор различных результатов, в которых частота появления электрона в заданном месте будет функцией плотности вероятности электронной волны. Если функция плотности вероятности для волны (или, точнее, квадрат плотности вероятности) для точки А в два раза больше, чем для точки В, то при многократном повторении опыта мы увидим, что электрон будет обнаруживаться в точке А в два раза чаще, чем в точке В. Точный результат эксперимента не может быть предсказан; лучшее, что можно сделать — предсказать вероятность данного возможного исхода».

Теперь допустим, (чисто гипотетически), что нам, как экспериментаторам, более желательно, чтобы электрон оказался в точке «В», где плотность вероятности в два раза меньше. Если не оказывать никакого влияния на ход проведения эксперимента, то в точке «А» он будет обнаруживаться в два раза чаще. Если суметь оказать влияние на траекторию электрона в сторону точки «В»[84], всё равно полного «математически точного» влияния на желаемый результат не будет, поскольку помимо более вероятного положения «А» существует ещё выведенная учёными неопределённость. Иными словами, в научно-математической постановке данного вопроса с позиций квантовой вероятности никогда не существует полной гарантии получения желаемого результата.

Именно с последним и не мог согласиться Эйнштейн, который также являлся представителем атеистической науки. Он и подобные ему учёные искали и ищут до сих пор математические модели гарантированного просчёта работы Вселенной во всех её аспектах — от макромира до микромира[85]. Эйнштейн до конца своих дней был сторонником научно точного получения однозначных результатов поведения материи. Правда он теоретически этого результата не достиг, ограничившись выражением «Он [Бог] не бросает кости».

Парадокс в том, что принципиально это выражение верно, т.е. Вселенная это не хаос случайностей. Определённость состоит в том, в том, что существует Матрица возможных состояний материи, которую учёные увидели как квантовую вероятность или меру неопределённости поведения микрочастицы. И всё-таки учёные пошли по пути Эйнштейна, продолжив поиск математически точной универсальной “формулы” работы Вселенной (Теория суперструн), допустив в её работу вероятностную составляющую «размазанных частиц»:

«Однако если математическое выражение для функции плотности вероятности известно точно, то даже при такой неопределённости исходов вероятностный прогноз может быть проверен путём многократного повторения эксперимента, что позволяет экспериментально определить вероятность того или иного конкретного результата. Всего через несколько месяцев после появления гипотезы де Бройля, Шрёдингер сделал важный шаг в этом направлении, предложив уравнение, которое определяет форму и эволюцию таких вероятностных волн, или, как они теперь называются, волновых функций. Вскоре уравнение Шрёдингера и вероятностная интерпретация были использованы для получения фантастически точных предсказаний. Таким образом, к 1927 г. классическая наивность была утрачена. Ушли те дни, когда Вселенная представлялась работавшим как часы механизмом, объекты которого, приведённые в движение в какой-то момент в прошлом, покорно следовали к неизбежному, единственным образом определяемому пункту назначения. Согласно квантовой механике Вселенная развивается в соответствии со строгими и точными математическими законами, но эти законы определяют только вероятность того, что может наступить то или иное конкретное будущее, и ничего не говорят о том, какое будущее наступит в действительности».

Вот в этом месте учёным бы и задаться вопросом: а кто, что, какие факторы устойчиво по предсказуемости управляют выбором конкретного будущего из всей вероятностной картины и можно ли определить не только вероятностную картину будущего, но и метод управления его конкретным выбранным вариантом? Ведь выбирает же каждая отдельная частица своё место на общей картине распределения плотностей вероятности. Точного ответа на эти вопросы наука не даёт, да и не может дать: это не в компетенции научных изысканий[86]. Мнения учёных разделились и согласно каждому из мнений стали развиваться околонаучные идейные течения, одно из которых мы рассмотрим в следующей главе (это идеи книги «Что мы вообще знаем?»).

«Тем не менее, споры о том, что же в действительности представляет собой квантовая механика, не утихают. Все согласны в том, как использовать уравнения квантовой механики для получения точных предсказаний. Нет согласия в вопросах о том, что в действительности представляют собой волновые функции, каким образом частица «выбирает», какому из многих вариантов будущего ей следовать. Нет согласия даже в вопросе о том, действительно ли она выбирает или вместо этого разделяется, подобно разветвляющемуся руслу реки, и живёт во всех возможных будущих, в вечно расширяющемся мире параллельных вселенных. Эти интерпретации сами по себе заслуживают отдельной книги, и, в действительности, есть немало превосходных книг, пропагандирующих тот или иной взгляд на квантовую теорию. Но совершенно определённым кажется тот факт, что независимо от интерпретации квантовой механики, она неопровержимо доказывает, что Вселенная основана на принципах, которые являются неестественными с точки зрения повседневного опыта».

⇐ Предыдущая 165 166 167 168 169170171 172 173 174 Следующая ⇒

Date: 2015-09-18; view: 336; Нарушение авторских прав

mydocx.ru - 2015-2024 year. (0.015 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию