Калибровочные поля

Калибровочные поля - поля обеспечивающие инвариантность теории относительно калибровочных преобразований. Простейший пример калибровочного поля –электромагнитное поле 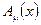связанное с абелевой (коммутативной) калибровочной группой .

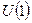Калибровочные преобразования –преобразования полей, зависящих от пространственно-временной точки х, которые описывают переход к новому базису в пространстве внутренних симметрий. сопровождающийся появлением дополнительного, калибровочного, поля.

Требование локальной калибровочной инвариантности выполняется только в том случае, когда во всех производных, действующих на свободные поля в лагранжиане осуществлена замена:

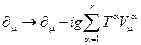
где 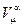–калибровочные поля; 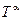-генераторы группы симметрии в матричном представлении, соответствующем свободому полю; 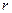- размерность группы.

Расслоения являются геометрической конструкцией адекватной идее калибровочного поля. Калибровочное поле есть связность в главном расслоении со структурной группой 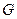определяющей калибровочное преобразование.

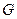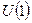
В классической электродинамике группа ~ -унитарная группа

В теории Янга-Миллса 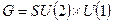полупростая группа Ли.

Геометрическая формулировка теории калибровочных полей.

Согласно физическому принципу относительности реальной физической конфигурации отвечает класс калибровочно эквивалентных конфигураций. Условие выбора однозначного представителя в каждом классе эквивалентных конфигураций, необходимое при вычислении континуальных интегралов, эквивалентно построению сечений в соответствующем расслоении. Локально такие сечения всегда существуют. Глобальных сечений (калибровок) построить нельзя. Это означает, например, что «не существует рыбы со сплошной чешуей».

Пример 3. В каждой точке многообразия М вводят репера из ортонормированных касательных векторов 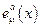. где ,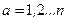

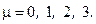
метрика плоского пространства.

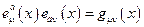-метрический тензор на М.

Вектора 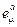-образуют базис касательного пространства 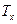состоящего из всех векторов касательных к М в точке 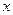.Этот репер называется тетрадой.

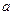-«лоренцовый» индекс, поднимает и опускает .

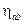индекс пространства-времени поднимает и опускает .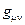

Date: 2015-09-05; view: 581; Нарушение авторских прав