Приложение 1 Суперматематика. Алгебра Грассмана. Расслоение. Калибровочные поля

Суперматематика -математический аппарат суперсимметричных теорий состоящий из алгебры и анализа с коммутирующими и антикоммутирующими переменными.

Рассмотрим ассоциативную алгебру А порожденную образующими 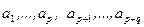. Первые р образующие являются четными. Остальные 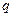образующие нечетные. Справедливы следующие правила:

1.число чет. элемент = чет. элемент

2.число нечет. элемент = нечет. элемент

3чет элем+чет элем= чет элем

4.нечет элем+нечет элем=нечет элем

5.чет 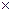чет=чет элем

6.нечет 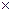нечет=чет элем

7.чет 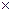нечет=нечет 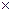чет=нечет элем

Любой элемент алгебры А может быть представлен единственным образом в виде суммы четного и нечетного элементов.

Алгебра А, в которой определено понятие четности называется 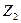-градуированной алгеброй.

Алгебра Грассмана – алгебра, порожденная антикоммутирующими образующими 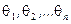, одна из простейших градуированных ассоциированных алгебр с единицей.

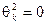, для любого к.

Размерность алгебры Грассмана как линейного пространства равна .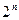

базис состоит из 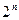одночленов:

1, , , ,…, .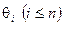

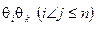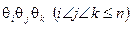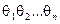Любой элемент алгебры Грассмана можно представить в виде конечной суммы

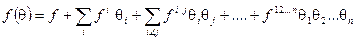
Интеграл на грассмановой алгебре задается правилами Березина

,

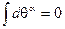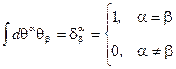
Кратный интеграл понимается как повторный. Возможно интегрирование по частям.

Справедлива формула для любого грассманового числа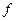

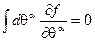
Интегрирование по грассмановым переменным эквивалентно дифференцированию:

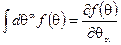
Интегрирование по грассмановым переменным позволяет построить функциональный интеграл, представляющий функцию Грина фермионных полей.

Дельта-функция Грассмана 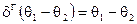действует как обычная дельта-функция:

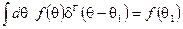
и удовлетворяет равенству .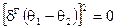

Расслоение (расслоенное пространство) – нетривиальная топологическая структура необходимая при описании взаимодействия между пространственными и внутренними степенями свободы физической системы.

Расслоение 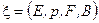-составной объект, включающий:

Е –пространство расслоения,

В – база расслоения,

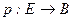-непрерывное отображение пространства расслоения Е в базу В,

пространство 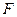- слой отображения.

Над каждой точкой базы можно определить полный прообраз 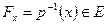, принадлежащий пространству расслоения Е.

Множество называется слоем над точкой х.

Локально расслоение устроено как прямое произведение .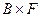

В расслоении можно определить обратное к р непрерывное отображение 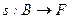, такое что 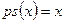для любой точки .

Отображение 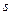называется сечением в расслоении пространства Е.

Наиболее интересны расслоения, у которых в слое действует группа преобразований слоя 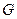. Слои над различными точками должны быть гомеоморфны друг другу. (преобразовываться друг в друга).

Интуитивно расслоение – это объединение слоев параметризованных точками базы и склеенных под действием группы преобразования слоев 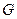. Наглядно это «рыба покрытая многослойной чешуей». 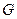-структурная группа расслоения.

Расслоение 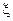называется главным, если слой расслоения совпадает с группой .

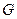Date: 2015-09-05; view: 726; Нарушение авторских прав