Комментарии. Возможность того, что наша Вселенная представляет собой лист, парящий в многомерном пространстве, восходит к статье двух знаменитых советских физиков В

Возможность того, что наша Вселенная представляет собой лист, парящий в многомерном пространстве, восходит к статье двух знаменитых советских физиков В. А. Рубакова и М. Е. Шапошникова «Do We Live Inside a Domain Wall?» (V A. Rubakov and М. E. Shaposhnikov, «Physics Letters В» 125 (May 26, 1983): 136) и не использует теорию струн. Рассматриваемый в главе 5 сценарий возникает из теоретико-струнных построений середины 1990-х годов.

Эта цитата взята из мартовского выпуска «Literary Digest» 1933 года. Следует отметить, что точность цитаты недавно была поставлена под сомнение датским историком науки Хельге Крагхом (см. его книгу: Helge Kragh, «Cosmology and Controversy». Princeton: Princeton University Press, 1999), который считает, что она может являться перефразировкой более ранней заметки в газете «Newsweek» того же года, где Эйнштейн высказывался о происхождении космических лучей. Однако доподлинно известно, что в этом же году Эйнштейн отрёкся от веры в статичную вселенную и принял динамичную космологию, возникающую из его исходных уравнений общей теории относительности.

Этот закон определяет силу гравитационного притяжения F между двумя объектами с заданными массами m 1 и m 2 и расстоянием r между ними. Математически закон имеет вид F = Gm 1 m 2/ r 2, где G обозначает константу Ньютона — экспериментально измеренное число, характеризующее силу гравитационного взаимодействия.

Для математически подкованного читателя приведём уравнения Эйнштейна:

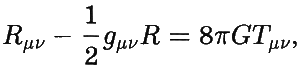
где g — это метрика пространства-времени, Rμν — тензор кривизны Риччи, R — скалярная кривизна, G — константа Ньютона, Tμν — тензор энергии-импульса.

За десятилетия, прошедшие с момента этого знаменитого подтверждения общей теории относительности, возникли вопросы, касающиеся надёжности полученных результатов. Чтобы увидеть световой луч от удалённой звезды, огибающий Солнце, наблюдения должны были проводиться во время солнечного затмения; к сожалению, плохая погода затруднила получение чётких фотографий затмения 1919 года. Вопрос в том, могли ли Эддингтон и его сотрудники внести систематическую ошибку под влиянием ожидаемого результата: отбраковывая фотографии, кажущиеся ненадёжными по причине интерференции, вызванной погодными условиями, они могли бы исключить несоразмерное количество фотографий с данными, которые казались противоречащими теории Эйнштейна. Недавнее подробное исследование Даниэля Кеннефика (см.: www.arxiv.org, paper arXiv:0709.0685, в котором, помимо прочих рассмотрений, делается современная переоценка фотографических пластинок, сделанных в 1919 году) убедительно свидетельствует что подтверждение теории, сделанное в 1919 году, на самом деле является надёжным.

Для заинтересованного читателя приведём уравнения Эйнштейна общей теории относительности, которые в рассматриваемом случае выглядят так:

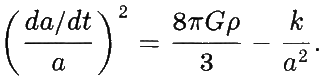
Переменная a (t) является масштабным фактором вселенной — её значение, как указывает название, устанавливает масштаб расстояния между объектами (если значения a (t) в два разных момента времени отличаются, например, в 2 раза, то расстояние между двумя частными галактиками будет отличаться между этими временами также в 2 раза), G — это константа Ньютона, ρ — плотность материи/энергии, и k является параметром, значение которого может быть 1, 0 или −1, в зависимости от того, является ли форма пространства сферической, евклидовой («плоской») или гиперболической. Обычно считается, что вид этого уравнения был найден Александром Фридманом и, собственно, называется уравнением Фридмана.

Внимательный читатель может отметить два момента. Во-первых, в общей теории относительности, как правило, мы определяем координаты, которые сами зависят от находящегося в пространстве вещества: мы используем галактики в качестве носителей координат (как будто на каждой галактике «нарисован» частный набор координат — так называемые движущиеся системы координат). Поэтому для задания определённой области пространства обычно ссылаются на присутствующую в ней материю. Тогда более точная перефразировка текста такова: область пространства, в которой находится некоторая группа из N галактик в момент времени t 1, будет иметь больший объём в более поздний момент времени t 2. Во-вторых, интуитивно понятное утверждение, касающееся плотности материи и энергии, изменяющиеся при расширении или сжатии пространства, содержит неявное предположение насчёт уравнения состояния материи и энергии. Есть ситуации и скоро мы столкнёмся с одной из них, когда пространство может расширяться или сжиматься, а плотность некоторого вклада энергии — плотность энергии так называемой космологической постоянной — остаётся неизменной. Действительно, есть даже более экзотические сценарии, в которых пространство расширяется а плотность энергии при этом растёт. Такое происходит, потому что при определённых обстоятельствах гравитация служит источником энергии. Важный момент этого параграфа состоит в том, что уравнения общей теории относительности в исходном виде противоречат статичной вселенной.

Вскоре мы увидим, что Эйнштейн отказался от статичной вселенной, столкнувшись с астрономическими данными, согласно которым вселенная расширяется. Однако, следует отметить, что его опасения насчёт статичной вселенной предшествовали получению этих данных. Физик Виллем де Ситтер указал Эйнштейну, что его статичная вселенная нестабильна: стоит её слегка толкнуть, и она начнёт расти или сжиматься. Физики избегают решений, которые могут существовать лишь в идеальных, неискажённых условиях.

В модели Большого взрыва расширение пространства вовне во многом подобно движению вверх подброшенного мяча: сила притяжения гравитации тянет обратно движущийся вверх мяч, и тем самым замедляет его движение; аналогичным образом сила притяжения гравитации действует на разлетающиеся галактики и тем самым тормозит их движение. Ни в одном из случаев движение вперёд не требует отталкивающей силы. Однако вы всё равно можете спросить: мяч был запущен вверх рукой, а что «запустило» пространство и его расширение вовне? Мы вернёмся к этому вопросу в главе 3, где увидим, что современная теория постулирует непродолжительную вспышку гравитационного отталкивания, действующего в самые ранние моменты космической истории. Мы также увидим, что более точные данные свидетельствуют о том, что расширение пространства не замедляется со временем, что приводит к удивительному — и это станет ясно в последующих главах — воскрешению потенциально глубокого смысла космологической постоянной.

Открытие пространственного расширения стало поворотным пунктом в современной космологии. Помимо открытий Хаббла, это достижение основывалось на работе и идеях многих других учёных, включая Весто Слайфера, Харлоу Шэпли и Мильтона Хумасона.

Двумерный тор обычно изображается как пустой бублик. Двухшаговый процесс показывает, что эта картинка согласована с приведённым в тексте книги описанием. Когда, достигнув правого края экрана, вы попадаете назад на левый край, это равносильно отождествлению всего правого края с левым краем. Если бы экран был гибким (например, из тонкого пластика), то такое отождествление могло бы быть буквальным, если скатать экран в цилиндр и объединить вместе правый и левый края. Когда, ступив на верхний край, вы попадаете в нижний, то это тоже равносильно отождествлению этих краёв. Это достигается явным образом на втором шаге, в котором мы скручиваем цилиндр и соединяем верхний и нижний круговые края. Получившаяся фигура выглядит как обычный бублик. Обманчивый аспект этих манипуляций состоит в том, что поверхность бублика выглядит искривлённой; если его поверхность покрыть отражающей краской, то ваше отражение будет искажено. Это артефакт реализации тора в виде объекта, расположенного в объемлющем трёхмерном пространстве. В действительности, являясь двумерной поверхностью, тор не искривлён. Он плоский. Что очевидно, если его представить в виде плоского экрана для видеоигр. Именно поэтому в тексте книги я выбрал более фундаментальное описание в виде фигуры, края которой попарно отождествляются.

Искушённый в математике читатель заметит, что под словами «подходящим образом нарезать и скомпоновать» я подразумеваю факторпространства, которые возникают при факторизации односвязных накрывающих пространств по дискретным группам изометрии.

Приведённое количество справедливо для текущей эры. В более ранней Вселенной критическая плотность была выше.

Если бы Вселенная была статична, то свет, путешествующий в течение последних 13,7 миллиардов лет и только сейчас достигший нас, действительно был бы излучён с расстояния в 13,7 миллиардов световых лет. В расширяющейся вселенной, в то время, пока свет находится в пути, испустивший его объект продолжает отдаляться миллиарды лет. Таким образом, на момент, когда мы принимаем этот свет, объект находится ещё дальше — значительно дальше, — чем 13,7 миллиардов световых лет. Вычисления с помощью общей теории относительности показывают, что этот объект (допустим, что он всё ещё существует и постоянно движется вместе с расширяющимся пространством) будет теперь находиться на расстоянии примерно 41 миллиарда световых лет. В этом смысле, наблюдаемая Вселенная имеет диаметр примерно 82 миллиарда световых лет. Свет от объектов, находящихся дальше, ещё не успел до нас дойти, и поэтому они находятся за пределами нашего космического горизонта.

Образно говоря, можно считать, что в силу квантовой механики частицы всегда находятся в состоянии, которое мне нравится называть «квантовым дрожанием»: что-то вроде неизбежных случайных квантовых вибраций, что придаёт самому понятию частицы с определённым положением и скоростью (импульсом) приближённый смысл. В этом смысле изменения в положении/скорости, достаточно малые, чтобы быть на равных с квантовыми флуктуациями, являются квантово-механическим «шумом» и, следовательно, не имеют значения.

На более точном языке, если погрешность в измерениях положения умножить на погрешность в измерениях импульса, то результат — неопределённость — всегда больше, чем число, называемое постоянной Планка (в честь Макса Планка, одного из пионеров квантовой физики). Это, в частности, означает, что точное разрешение в процессе измерения положения частицы (небольшая погрешность) обязательно приведёт к большой неопределённости при измерении импульса частицы и, за компанию, её энергии. Поскольку энергия всегда ограничена, разрешение при измерении положения, таким образом, тоже является ограниченным.

Также отметим, что эти понятия всегда будут применяться в конечной пространственной области — как правило, в областях, размер которых сопоставим с современным космическим горизонтом (как в следующем разделе). Область конечного размера, пусть даже большая, подразумевает максимальную неопределённость при измерении положения. Если предполагается, что частица находится в данной области, то неопределённость её положения конечно же будет не больше размера самой области. Согласно принципу неопределённости, такая максимальная неопределённость в положении приводит к минимальной неопределённости при измерении импульса. Помимо ограниченного разрешения при измерении местоположения, мы видим редукцию от бесконечного к конечному числу возможных различных конфигураций положений и скоростей частицы.

Вы всё ещё можете задаваться вопросом о том, что препятствует построению прибора, способного измерять положения частицы с ещё большей точностью. Это также касается энергии. Как описано в книге, если вы хотите измерить положение частицы с большей точностью, необходимо использовать более точный прибор. Для определения местоположения мухи в комнате можно включить обычный верхний свет. Для определения положения электрона необходимо осветить его узким лучом мощного лазера. Для ещё более точного определения положения электрона надо использовать ещё более мощный лазер. Когда более мощный лазер бьёт по электрону, его скорость сильно искажается. Таким образом, ключевой момент здесь в том, что точность определения положения частицы достигается за счёт огромных изменений скорости частицы — и, следовательно, огромных изменений её энергии. Если есть предел того, сколько энергии может иметь частица, а такой предел есть всегда, то также есть предел того, насколько точно можно измерить её положение.

Таким образом, ограниченность энергии в ограниченной пространственной области приводит к конечному разрешению при измерении как положения, так и скорости.

Наиболее прямой способ проделать это вычисление состоит в использовании результата, который без привлечения технических подробностей будет описан в главе 9: энтропия чёрной дыры — логарифм числа различных квантовых состояний — пропорциональна площади её поверхности, измеренной в единицах планковской площади. Заполняющая наш космический горизонт чёрная дыра будет иметь радиус примерно 1028 сантиметра, или примерно 1061 планковских длин. Таким образом, её энтропия будет примерно 10122 в единицах планковской площади. Следовательно, полное число различных состояний составляет примерно 10, возведённое в степень 10122, или 1010122.

Можно поинтересоваться, почему не учитываются поля. Как мы увидим, описания частиц и полей дополнительны друг к другу — поле может описываться в терминах определённых частиц, из которых оно состоит, подобно тому как океанские волны могут описываться в терминах составляющих их молекул воды. Выбор описания в терминах частиц или полей является в основном вопросом удобства.

Расстояние, проходимое светом за заданный промежуток времени, сильно зависит от скорости расширения пространства. В последующих главах мы обсудим доводы, указывающие на то, что темп пространственного расширения ускоряется. Если так, то существует предел того, насколько далеко свет может распространиться в пространстве, даже если ждать сколь угодно долго. Удалённые области пространства будут удаляться от нас так быстро, что излучаемый нами свет не сможет достичь их; аналогичным образом испущенный ими свет не сможет достичь нас. Это будет означать, что космические горизонты — та часть пространства, с которой можно обмениваться световыми сигналами, — не будут расти бесконечно. (Заинтересовавшийся читатель может найти соответствующие формулы в комментарии 66.)

Дж. Эллис и Дж. Бандрит исследовали повторяющиеся миры в бесконечной классической вселенной; Ж. Гаррига и А. Виленкин изучали такие миры в квантовом контексте.

В ранних работах Дикке рассматривал идею осциллирующей Вселенной, которая многократно проходит через вереницу циклов Большой взрыв—расширение—сжатие—схлопывание и снова Большой взрыв. В любом цикле будет присутствовать заполняющее пространство остаточное излучение.

Следует отметить, что хотя у галактик нет реактивных двигателей, в общем случае они движутся чуть быстрее, чем ожидается из расширения пространства — как правило, это результат крупномасштабных межгалактических гравитационных сил, а также внутреннего движения вращающегося газового облака, из которого образуются звёзды в галактиках. Скорость такого движения называется пекулярной и, как правило, она достаточно мала, поэтому в космологическом анализе ею можно смело пренебречь.

Проблема горизонта довольно тонкая, и приведённое мной описание решения на основе инфляционной космологии несколько отличается от стандартного, поэтому, возможно, читателя заинтересует чуть более подробное обсуждение этого вопроса. Сначала опять постановка проблемы: рассмотрим две области в ночном небе, настолько удалённые друг от друга, что они никогда не вступали в контакт. Для определённости скажем, что в каждой области находится наблюдатель, который контролирует термостат, поддерживающий температуру в его области. Эти наблюдатели хотят, чтобы две данные области имели одинаковую температуру, но поскольку наблюдатели не имели возможности контактировать, они не знают на какую температуру устанавливать свои термостаты. Естественная идея состоит в том, что поскольку миллиарды лет назад наблюдатели находились гораздо ближе, то тогда им было проще установить контакт и сравнять температуры в своих областях. Однако, как отмечалось в основном тексте, в стандартной теории Большого взрыва эти рассуждения не проходят. И этому есть причины. В стандартной теории Большого взрыва Вселенная расширяется, но в силу гравитационного притяжения темп расширения со временем замедляется. Это очень похоже на подбрасывание мяча вверх. Во время подъёма он сначала быстро удаляется от вас, но в силу притяжения Земли постепенно замедляется. Замедление пространственного расширения имеет серьёзные последствия. Для пояснения я воспользуюсь аналогией с подброшенным мячом. Представьте, что мяч достигает верхней точки за шесть секунд. Поскольку изначально (после того как отрывается от вашей руки) он двигался быстро, он может пройти первую половину расстояния за две секунды, но из-за уменьшения скорости пройдёт четыре секунды, прежде чем он одолеет вторую половину пути. Таким образом, на половине временного интервала, через три секунды, он пролетел больше половины пути. Аналогичным образом происходит процесс замедляющегося во времени пространственного расширения: в середине космической истории два наших наблюдателя будут разделены расстоянием бо́льшим, чем половина современного расстояния между ними. Давайте подумаем, что это значит. Два наблюдателя будут ближе друг к другу, но им будет тяжелее — а не легче — установить контакт. Посылаемый одним из наблюдателей сигнал будет располагать половиной от прошедшего интервала времени для достижения второго наблюдателя, но расстояние, которое он должен будет преодолеть, больше половины от современного расстояния. Половина времени для взаимодействия на расстоянии, превышающем половину текущего расстояния между ними, осложняет установление контакта между наблюдателями.

Таким образом, расстояние между наблюдателями — лишь один из факторов при анализе возможности наблюдателей влиять друг на друга. Другой фактор — время, прошедшее с момента Большого взрыва, поскольку это ограничивает дальность распространения сигнала. В стандартной теории Большого взрыва, хотя в прошлом всё действительно располагалось ближе друг к другу, Вселенная также и расширялась быстрее, поэтому, пропорционально говоря, для распространения влияния было меньше времени.

Решение этого вопроса, предложенное в инфляционной космологии, состоит в добавлении некоторой фазы в самые ранние моменты космической истории, в которой темп расширения не замедляется, как скорость подброшенного вверх мяча; наоборот, пространственное расширение начинается неспешно, а затем постепенно наращивает скорость: расширение ускоряется. Согласно только что приведённым рассуждениям, на половине пути такой инфляционной фазы два наших наблюдателя будут разделены расстоянием меньшим половины расстояния между ними в момент завершения инфляционной фазы. А если есть половина времени для распространения сигнала на менее чем половину расстояния, это означает, что в ранние моменты времени контакт мог быть легче установлен. Можно сказать, что ускорение расширения в более ранние моменты времени означает, что для распространения сигнала было больше времени, а не меньше. Это позволяло удалённым на настоящий момент областям легко контактировать в ранней Вселенной, что объясняет их одинаковую температуру сейчас.

Поскольку по сравнению со стандартной теорией Большого взрыва ускоренное расширение приводит к ещё большему пространственному расширению, эти области будут гораздо ближе в начальный момент при инфляции, чем в аналогичный момент времени в стандартной теории Большого взрыва. Эта разница в расстоянии в ранней Вселенной является эквивалентным способом для понимания того, почему контакт между областями, невозможный при стандартном Большом взрыве, легко достигается в инфляционной теории. Если в некоторый момент после начала расстояние между двумя областями меньше, им легче обмениваться сигналами.

Применяя уравнения, описывающие расширение в произвольные ранние моменты времени (представьте, для определённости, что пространство имеет форму сферы), мы увидим, что две области в инфляционной модели будут удаляться друг от друга медленнее, чем при стандартном Большом взрыве: именно поэтому они удаляются на меньшее расстояние по сравнению с теорией Большого взрыва. В этом смысле в инфляционном подходе есть период времени, когда темп разлёта областей меньше, чем в картине обычного Большого взрыва.

При описании инфляционной космологии очень часто всё внимание целиком сосредоточено на фантастическом увеличении скорости расширения по сравнению со стандартными подходами, а не на уменьшении. Различие в описании возникает из того, какие физические свойства двух подходов сравниваются. Если сравнить траектории двух областей, расположенных в ранней Вселенной на некотором расстоянии друг от друга, то в инфляционной теории эти области разлетаются гораздо быстрее, чем в стандартной теории Большого взрыва; на сегодняшний день они находятся гораздо дальше друг от друга, чем после обычного Большого взрыва. Но если рассматривать области, расположенные на определённом расстоянии сегодня (подобно двум участкам в противоположных концах ночного неба), то становится важным приведённое мной описание. А именно: в определённый момент времени в очень ранней Вселенной эти области были гораздо ближе друг к другу, и в теории с инфляционным расширением разлетались гораздо медленнее, чем в теории без такового. Роль инфляционного расширения в том, чтобы компенсировать медленный старт, разгоняя затем эти области быстрее и быстрее, гарантируя, что они окажутся в тех же местах на небе как и в стандартной теории Большого взрыва.

Более полное обсуждение проблемы горизонта включало бы подробное рассмотрение условий возникновения инфляционного расширения, а также последующих процессов, которые, например, приводят к возникновению реликтового излучения. Однако цель приведённых выше рассуждений — подчеркнуть существенное различие между ускоряющимся и замедляющимся расширением.

Отметим, что, сжимая пакет, вы добавляете в систему энергию, и поскольку масса и энергия приводят к гравитационному искривлению, то увеличение веса будет частично происходить благодаря увеличению энергии. Однако увеличение давления также даёт вклад в увеличение веса. (Точности ради заметим, что следует представлять этот «эксперимент» в вакуумной камере, поэтому нет необходимости рассматривать выталкивающую силу со стороны воздуха вокруг пакета.) В повседневных примерах обсуждаемое увеличение веса крайне мало. Однако на космических масштабах оно может оказаться весьма значительным. На самом деле, оно играет роль при объяснении того, почему в определённых ситуациях звёзды обязательно схлопываются в чёрные дыры. Как правило, равновесие в звёздах поддерживается благодаря балансу между давлением, направленным наружу, порождённым ядерными процессами в звёздном ядре, и направленной внутрь гравитацией, порождаемой массой звезды. По мере того как звезда расходует ядерное топливо, положительное давление падает, что приводит к её сжатию. При этом вещество внутри звезды сжимается плотнее, вследствие чего гравитационное притяжение возрастает. Для избежания дальнейшего сжатия, необходимо дополнительное давление наружу (что называется положительным давлением, как в следующем абзаце в основном тексте). Однако дополнительное положительное давление само создаёт дополнительную силу гравитационного притяжения и таким образом приводит к необходимости ещё большего дополнительного положительного давления. В определённых ситуациях это приводит к спиральной нестабильности, и положительное давление, на котором обычно держится противодействие звезды внутреннему гравитационному сжатию, настолько усиливает внутреннее притяжение, что становится неизбежным полный гравитационный коллапс. Звезда коллапсирует, и образуется чёрная дыра.

В описанном только что подходе к инфляции нет фундаментального объяснения, почему значение поля инфлатона должно находиться на возвышенной части кривой потенциальной энергии, а также нет объяснения, почему кривая потенциальной энергии имеет именно такую форму. Всё это предположения теории. В последующих версиях теории инфляции, в особенности версии, разработанной Андреем Линде, которая называется хаотическая инфляция, более «обычная» кривая потенциальной энергии (параболическая форма без плоских участков, выводимая из простейших математических уравнений для потенциальной энергии) также может приводить к инфляции. Для запуска инфляционного расширения значение поля инфлатона также должно находиться высоко на этой кривой потенциальной энергии, однако неимоверно горячая среда в ранней Вселенной естественным образом создаёт для этого все условия.

Внимательного читателя заинтересует следующая подробность. Быстрое расширение пространства в инфляционной космологии приводит к сильному остыванию (подобно тому как быстрое сжатие пространства, или чего-нибудь ещё, вызывает повышение температуры). Однако, когда инфляция подходит к завершению, поле инфлатона колеблется около минимума своей кривой потенциальной энергии, трансформируя свою энергию в газ частиц. Этот процесс называется «повторным разогревом», потому что порождённые таким образом частицы получают кинетическую энергию и, следовательно, могут характеризоваться температурой. По мере того как пространство продолжает расширяться обычным (не-инфляционным) способом, в сценарии Большого взрыва температура газа частиц постепенно снижается. Однако важный момент в том, что возникшая при инфляции однородность задаёт однородные условия для этого процесса, и поэтому приводит к однородным результатам.

Алан Гут осознал бесконечную природу инфляции; Пол Стейнхард предложил её математическую реализацию в определённом контексте; Александр Виленкин описал её в самых общих терминах.

Значение поля инфлатона определяет количество энергии и отрицательное давление, которыми оно наполняет пространство. Чем больше энергия, тем быстрее темп расширения пространства. В свою очередь быстрое расширение пространства оказывает обратное влияние на само поле инфлатона: чем быстрее расширение пространства, тем сильнее флуктуации значений поля инфлатона.

Давайте рассмотрим вопрос, который, возможно, уже возникал у вас, и к которому мы вернёмся в главе 10. Когда пространство испытывает инфляционное расширение, его полная энергия возрастает: чем больше объём пространства, заполненного полем инфлатона, тем больше полная энергия (если пространство бесконечно, энергия тоже бесконечна — в этом случае следует говорить об энергии, содержащейся в конечной области пространства, по мере того как эта область растёт). Что естественным образом приводит к следующему вопросу: где источник энергии? В аналогичной ситуации с бутылкой шампанского источник дополнительной энергии в бутылке обеспечивается усилиями ваших мускулов. Что играет роль мускулов в расширяющемся космосе? Ответ — гравитация. Подобно тому как ваши мускулы обеспечивают расширение доступного пространства в бутылке (путём вытаскивания пробки), гравитация является движущей силой расширения доступного пространства в космосе. При этом важно понимать, что энергия гравитационного поля может быть сколь угодно отрицательно большой. Рассмотрим две частицы, падающие друг на друга при взаимном гравитационном притяжении. Гравитация заставляет эти частицы приближаться друг к другу всё быстрее, при этом их кинетическая энергия становится всё более положительной. Гравитационное поле может обеспечить частицы такой положительной энергией за счёт расходования своего собственного энергетического резерва, который в таком процессе становится сколь угодно отрицательным: чем сильнее частицы сближаются, тем более отрицательной становится гравитационная энергия (эквивалентно, тем более положительна энергия, которую надо приложить, чтобы преодолеть силу гравитации и заново разнести частицы). Таким образом, гравитация подобна банку, который предоставляет безграничную кредитную линию и может давать бесконечное число денег; гравитационное поле может дать бесконечное количество энергии, потому что его собственная энергия может становиться при этом всё более отрицательной. Именно в этом состоит источник энергии, запускающий инфляционное расширение.

Термин «ячейка-вселенная» не менее наглядно изображает процесс возникновения Вселенной в объемлющей среде, заполненной инфлатоном (был предложен Аланом Гутом).

Для математически подготовленного читателя отметим, что более точное описание горизонтальных осей на рис. 3.5 таково: рассмотрим двумерную сферу, состоящую из точек пространства в момент времени, когда реликтовое излучение начало свободно распространяться. Подобно любой двумерной сфере, удобный набор координат на этой поверхности — это угловые переменные сферической системы координат. Тогда температура реликтового излучения может рассматриваться как функция этих угловых переменных и, соответственно, может быть разложена в ряд Фурье по сферическим гармоникам Ylm (θ, ϕ). Вертикальная ось на рис. 3.5 отражает величину коэффициента каждой моды в этом разложении — перемещение вправо вдоль горизонтальной оси соответствует уменьшению углового разделения. Технические подробности могут быть найдены, например, в отличной книге Додельсона: Scott Dodelson, «Modern Cosmology». San Diego, Calif.: Academic Press, 2003.

Если более точно, не сила гравитационного поля сама по себе определяет замедление времени, а величина гравитационного потенциала. Например, если вы зависните внутри сферической полости в центре массивной звезды, то не будете вообще чувствовать гравитационную силу, но поскольку вы находитесь глубоко внутри ямы гравитационного потенциала, время для вас будет течь медленнее, чем для того, кто находится за пределами звезды.

Этот результат (и родственные идеи) был получен рядом исследователей в различных контекстах и наиболее чётко выражен Александром Виленкиным, а также Сидни Коулменом и Фрэнком де Луччией.

Напомним, что при обсуждении лоскутной мультивселенной предполагалось, что компоновки частиц варьируются случайным образом от лоскутка к лоскутку. Связь между лоскутной и инфляционной мультивселенными также позволяет прояснить это предположение. Пузырёк-вселенная образуется в данной области, когда падает значение поля инфлатона; когда это происходит, энергия инфлатона трансформируется в частицы. Точный набор этих частиц в любой момент времени определяется точным значением инфлатона во время процесса трансформации. Поскольку поле инфлатона испытывает квантовые флуктуации, при спускании оно начинает испытывать случайные колебания — такие же случайные колебания, которые приводят к образованию структуры из чуть более горячих и чуть более холодных пятнышек на рис. 3.4. Применительно к лоскуткам внутри пузырька-вселенной это будет соответствовать тому, что на значении инфлатона будут отражаться случайные квантовые колебания. Такая случайность обеспечит случайность получающихся распределений частиц. Именно поэтому мы ожидаем, что любая конфигурация частиц, например такая, которая отвечает за то, что мы видим вокруг нас прямо сейчас, будет повторяться так же часто, как любая другая.

Я благодарен Вальтеру Исааксону за личное обсуждение этого и ряда других исторических вопросов, связанных с Эйнштейном.

Давайте рассмотрим этот вопрос подробнее. Глэшоу, Салам и Вайнберг предположили, что электромагнитное и слабое взаимодействия являются проявлениями единого электрослабого взаимодействия. Электрослабая теория была подтверждена в экспериментах на ускорителе в конце 1970-х и начале 1980-х годов. Глэшоу и Джорджи пошли дальше и предложили, что электрослабое и сильное взаимодействия являются проявлениями ещё более фундаментального взаимодействия, в рамках подхода, который был назван великим объединением. Однако простейшая версия великого объединения была отброшена, когда учёным не удалось экспериментально подтвердить одно из предсказаний — что протоны должны время от времени распадаться. Тем не менее есть много других вариантов великого объединения, которые пока экспериментально не отвергнуты, например потому, что предсказываемая ими скорость распада протона настолько мала, что чувствительность современного экспериментального оборудования недостаточна для обнаружения распада. Однако даже если великое объединение не подкрепляется экспериментальными данными, уже нет никаких сомнений, что три негравитационных взаимодействия могут быть описаны на едином математическом языке квантовой теории поля.

Открытие теории суперструн дало толчок к развитию других, тесно связанных теоретических подходов, направленных на поиски единой теории фундаментальных взаимодействий. В частности, суперсимметричная квантовая теория поля и её гравитационное расширение (супергравитация) глубоко изучались в середине 1970-х годов. Суперсимметричная квантовая теория поля и супергравитация основаны на новом принципе суперсимметрии, который был открыт в рамках теории суперструн, но эти подходы подключают суперсимметрию к обычным теориям точечных частиц. Позже в этой главе мы кратко обсудим суперсимметрию, но для заинтересовавшихся читателей я здесь замечу, что суперсимметрия — это самая последняя из имеющихся симметрий (помимо вращательной симметрии, трансляционной симметрии, симметрии Лоренца и, в общем случае, симметрии Пуанкаре) в нетривиальной теории элементарных частиц. Она связывает частицы различных квантово-механических спинов и вскрывает глубокое математическое родство между частицами-переносчиками взаимодействий и частицами, из которых состоит материя. Супергравитация — это расширение суперсимметрии посредством включения гравитационного поля. В ранний период исследований по теории струн учёные осознали, что суперсимметрия и супергравитация возникают в низкоэнергетическом пределе теории струн. При низких энергиях протяжённость струны разглядеть нельзя, поэтому она выглядит как точечная частица. Соответственно, как будет обсуждаться в этой главе, применительно к низкоэнергетическим процессам математический аппарат теории струн преобразуется в аппарат квантовой теории поля. Учёные обнаружили, что поскольку суперсимметрия и гравитация выживают при таком преобразовании, то низкоэнергетические теории струн приводят к суперсимметричным квантовым теориям поля и супергравитации. Как будет обсуждаться в главе 9, связь между суперсимметричной теорией поля и теорией струн впоследствии стала ещё более глубокой.

Осведомлённый читатель может не согласиться с моим утверждением, что каждое поле ассоциируется с частицей. Более точное утверждение звучит так: малые флуктуации поля около локального минимума его потенциала обычно интерпретируются как возбуждения частиц. Этого определения будет достаточно для наших обсуждений. К тому же осведомлённый читатель заметит, что локализация частицы в точке сама по себе является идеализацией, потому что для этого потребуется — из принципа неопределённости — бесконечный импульс и энергия. Опять же суть в том, что в квантовой теории поля нет, в принципе, предела того, как можно в конце концов локализовать частицу.

Исторически математическая техника, известная как перенормировка (или ренормализация), была развита для устранения количественных проявлений жёстких (высокоэнергетичных) колебаний квантового поля на малых расстояниях. При применении к квантово-полевым теориям трёх негравитационных взаимодействий перенормировка устранила бесконечные величины, возникающие при различных вычислениях, что позволило физикам сделать фантастически точные предсказания. Однако, когда перенормировку применили к квантовым флуктуациям гравитационного поля, она оказалась неэффективной: метод не смог устранить бесконечности, возникающие при квантовых вычислениях с учётом гравитации.

С более современных позиций эти бесконечности рассматриваются несколько иначе. Физики осознали, что на пути к более глубокому пониманию законов природы разумно придерживаться той точки зрения, что любая теория приблизительна — если вообще значима — и скорее всего может описывать физические явления только вплоть до некоторого определённого масштаба (или только до некоторого энергетического масштаба). Явления за его пределами не могут описываться данной теорией. Согласно этой точке зрения, безрассудно применять данную теорию на расстояниях, меньших чем область применимости теории (или на энергиях, превышающих область применимости). С учётом таких встроенных отсеканий (подобно тем, что описаны в основном тексте) бесконечности никогда не будут возникать. Наоборот, все вычисления проводятся в теории, диапазон применимости которой обозначен с самого начала. Это означает, что предсказательная сила ограничена явлениями, находящимися в установленных теорией пределах, а на очень коротких расстояниях (больших энергиях) теория не работает. Окончательная цель полной теории квантовой гравитации состоит в устранении встроенных пределов и распространении предсказательной силы теории на произвольные масштабы.

Чтобы понять, откуда берутся эти конкретные числа отметим, что квантовая механика (см. главу 8) сопоставляет частице волну, и чем тяжелее частица, тем короче длина волны (расстояние между последовательными гребнями). Общая теория относительности Эйнштейна также сопоставляет длину произвольному объекту — это размер, до которого надо сжать объект, чтобы он стал чёрной дырой. Чем тяжелее объект, тем больше этот размер. А теперь возьмите частицу, которая описывается квантовой механикой, и представьте, что её масса медленно растёт. При этом квантовая волна частицы укорачивается, а её «размер чёрной дыры» увеличивается. При некоторой массе квантовая длина волны и размер чёрной дыры совпадут, что задаст тот уровень массы и размера, при котором квантово-механические и гравитационные рассмотрения одновременно важны. При проведении численной оценки такого мысленного эксперимента масса и размер оказываются равными тем значениям, которые озвучены в основном тексте — планковской массе и планковской длине соответственно. Забегая вперёд, скажу, что в главе 9 мы будем обсуждать голографический принцип. Основываясь на общей теории относительности и физике чёрных дыр, этот принцип утверждает, что существует очень определённое ограничение на количество физических степеней свободы, которые могут существовать внутри произвольной области пространства (это более точная версия рассуждений из главы 2 относительно количества различных конфигураций частиц в заданном объёме пространства; это также обсуждается в комментарии 15). Если этот принцип верен, то конфликт между общей теорией относительности и квантовой механикой может возникнуть прежде, чем расстояния станут малыми, а кривизны большими. Огромный объём пространства, заполненный газом частиц даже малой плотности, будет обладать, согласно квантовой теории, значительно бо́льшим количеством степеней свободы, чем позволяет голографический принцип (основанный на общей теории относительности).

Квантово-механический спин является достаточно тонким понятием. Трудно представить, что значит «вращающийся», особенно в квантовой теории поля, где частицы считаются точками. На самом деле, из экспериментов следует, что частицы могут обладать внутренним свойством, очень похожим на постоянный угловой момент. Более того, из квантовой теории следует, и эксперименты это подтверждают, что частицы могут иметь угловой момент, который является только целым кратным некоторой фундаментальной величины (константы Планка, делённой на 2). Поскольку классические вращающиеся объекты обладают внутренним угловым моментом (который, однако, не является постоянным — он изменяется при изменении вращательной скорости объекта), теоретики заимствовали название «спин» и применили его к аналогичной квантовой ситуации. Отсюда название «спиновый угловой момент». Хотя выражение «вращающийся как волчок» создаёт подходящий зрительный образ, более точно будет представлять, что частицы характеризуются не только их массой, электрическим зарядом, зарядом ядра, а также внутренним неизменным спиновым угловым моментом. Подобно тому как электрический заряд частицы является одним из её фундаментальных определяющих свойств, эксперименты демонстрируют, что таким же свойством является её спиновый угловой момент.

Напомним, что причиной напряжённости между общей теорией относительности и квантовой механикой являются мощные квантовые флуктуации гравитационного поля, которые сотрясают пространство-время настолько сильно, что традиционные математические методы перестают работать. Квантовая неопределённость говорит нам, что эти флуктуации становятся тем сильнее, чем меньше расстояние (именно поэтому эти флуктуации в обычной жизни не видны). Вычисления показывают, что именно энергичные флуктуации на расстояниях, меньше планковского масштаба, расстраивают наши математические инструменты (чем меньше расстояние, тем больше энергия флуктуаций). Поскольку в рамках квантовой теории поля частицы описываются как точки, не имеющие пространственного размера, расстояния, достижимые этими частицами, могут быть сколь угодно малыми, и, следовательно, ощущаемые ими квантовые флуктуации могут быть сколь угодно энергичными. В теории струн ситуация изменяется. Струны не являются точками — у них имеется пространственный размер. Это означает, что есть предел малости достижимого расстояния, даже в принципе, так как струна не может уместиться на расстоянии меньшем, чем её длина. В свою очередь самое малое достижимое расстояние задаёт предел того, насколько энергичными могут быть квантовые флуктуации. Этот предел оказывается достаточным, чтобы приручить неуправляемую математику, позволяя теории струн соединить квантовую механику и общую теорию относительности.

Если некий объект был бы по-настоящему одномерным, мы не смогли бы его видеть, потому что у него нет поверхности, от которой могли бы отражаться фотоны, и он не мог бы сам порождать фотоны посредством атомных переходов. Поэтому когда я говорю «увидеть», то подразумеваю все возможные способы наблюдения или экспериментирования, которые могли бы подтвердить пространственную протяжённость объекта. Тогда утверждение состоит в том, что любое пространственное измерение, меньшее чем разрешающая способность оборудования, не может быть обнаружено на эксперименте.

«What Einstein never knew», NOVA documentary, 1985.

Более точно, та составляющая компонента Вселенной, которая наиболее существенна для нашей формы жизни, была бы разительно другой. Поскольку известные частицы и объекты, из которых они состоят — звёзды, планеты, люди и так далее, — сводятся к менее чем 5 процентам массы Вселенной, такое нарушение не будет влиять на бо́льшую часть Вселенной, по крайней мере в том, что касается её массы. Однако, если рассматривать это влияние на жизнь в привычном нам виде, разница будет огромной.

Существуют некоторые умеренные ограничения, которые квантовая теория поля накладывает на свои внутренние параметры. Во избежание определённых типов неприемлемого физического поведения (нарушения закона сохранения, нарушения определённых преобразований симметрии и так далее) могут накладываться ограничения на заряды (электрические, а также ядерные) частиц теории. Более того, поскольку сумма вероятностей во всех физических процессах обязана быть равной 1, массы частиц также не могут быть любыми. Но даже при этом допустимые значения характеристик частиц варьируются достаточно широко.

Некоторые исследователи могут заметить, что хотя ни квантовая теория поля, ни текущее состояние теории струн не дают объяснения свойств частиц, этот вопрос более насущен для теории струн. Он достаточно сложен, но для заинтересованных читателей приведём краткое резюме. Свойства частиц в квантовой теории поля — например, их массы — задаются числами, которые подставляются в уравнения теории. Сам факт того, что уравнения квантовой теории поля допускают варьирование таких чисел, является математическим способом сказать, что квантовая теория поля не определяет массы частиц, а, наоборот, использует их в качестве начальных данных. В теории струн гибкость в выборе масс частиц имеет схожее математическое происхождение — уравнения допускают свободное варьирование некоторых чисел, — однако проявление этой гибкости более значимо. Свободно изменяющиеся числа — числа, которые могут изменяться без каких-либо затрат энергии — соответствуют наличию в теории безмассовых частиц. (Если вернуться к главе 3 к языку кривых потенциальной энергии, то представьте совершенно плоскую кривую, то есть горизонтальную линию. Подобно тому как прогулка по совершенно плоской поверхности не меняет вашей потенциальной энергии, изменение значения такого поля не приведёт к затратам энергии. Поскольку масса частицы соответствует кривизне кривой потенциальной энергии квантового поля вблизи её минимума, то кванты таких полей являются безмассовыми.) Избыточное число безмассовых частиц является особенно неприятным свойством любой предлагаемой теории, потому что есть строгие ограничения на такие частицы, вытекающие из экспериментальных данных, полученных на ускорителях, и космологических наблюдений. Чтобы теория струн была жизнеспособной, безмассовым частицам необходимо придать массу. В течение последних лет было предложено несколько механизмов генерации масс, основанных на потоках, пронизывающих дырки в пространствах Калаби–Яу дополнительных измерений. Я вернусь к этому в главе 5.

Возможно, что в экспериментах будут получены данные, которые сильно пошатнут нашу веру в теорию струн. Структура теории струн гарантирует, что определённые базовые принципы должны соблюдаться во всех физических явлениях. Среди них унитарность (сумма вероятностей всех возможных результатов в данном эксперименте должна быть равна 1) и локальная Лоренц-инвариантность (в достаточно малой области справедлива специальная теория относительности), а также более технические свойства, такие как аналитичность и кроссинг-симметрия (результат столкновения частиц должен зависеть от импульсов частиц таким образом, чтобы удовлетворялся некоторый набор математических критериев). Если будет обнаружено — возможно, на Большом адронном коллайдере, — что любой из этих принципов нарушается, то примирить полученные данные с теорией струн станет трудной задачей. (Согласовать эти данные со Стандартной моделью физики частиц, которая также использует эти принципы, будет столь же проблематично; однако здесь спасает допущение, что при достаточно высоких энергиях Стандартная модель должна уступить место некой новой физике, поскольку она не включает в себя гравитацию. Но если мы получим данные, конфликтующие с любым из перечисленных выше принципов, это будет указывать на то, что новая физика — это не теория струн.)

Когда говорят о центре чёрной дыры, то часто создаётся впечатление, что это некое место в пространстве. Но это не так. Центром чёрной дыры следует считать определённый момент времени. При пересечении горизонта событий чёрной дыры время и пространство (радиальное направление) меняются ролями. Если вы падаете в чёрную дыру, ваше радиальное движение являет собой движение во времени. Таким образом, вас толкает в центр чёрной дыры точно так же, как вас толкает к следующему моменту времени. В этом смысле центр чёрной дыры похож на последний момент времени.

По многим причинам энтропия является ключевым понятием в физике. В обсуждаемом случае энтропия используется как диагностика того, не упускает ли теория струн какую-нибудь существенную физику при описании чёрных дыр. Если бы так случилось, то результат вычислений беспорядка внутри чёрной дыры на основе струнной математики оказался бы неверным. Тот факт, что ответ точно совпадает с тем, что Бекенштейн и Хокинг вывели с помощью совсем других рассуждений, указывает на то, что теория струн успешно ухватила фундаментальное физическое описание. Это очень обнадёживающий результат. Более подробно об этом можно прочитать в книге «Элегантная Вселенная», глава 13.

Первое указание на парность форм Калаби–Яу возникло в работе Ланса Диксона, а также в независимой работе Вольфганга Лерхе, Николаса Уорнера и Кумруна Вафы. В моей работе с Роненом Плессером был предложен метод построения первого конкретного примера таких пар, которые мы назвали зеркальными парами, а соотношение между ними — зеркальной симметрией. Плессер и я также показали, что трудная задача, такая как определение числа сфер, которые можно упаковать в данную форму, неподъёмная при использовании одного из партнёров по паре, может стать гораздо легче на зеркальной форме. Этот результат был подхвачен Филиппом Канделасом, Ксенией де ла Осой, Полом Грином и Линдой Паркерс — они развили технику вычислений, основанную на равенстве, которое Плессер и я установили между «трудными» и «простыми» формулами. С помощью простой формулы они получили информацию о трудном партнёре, включая числа, связанные с упаковкой сфер, приведённые в основном тексте книги. За последующие годы зеркальная симметрия стала отдельной областью исследований, где было получено много важных результатов. Детальная история этого вопроса приведена в книге Шин-Туна Яу и Стива Надиса: Shing-Tung Yau and Steve Nadis, «The Shape of Inner Space». New York: Basic Books, 2010.

Утверждение теории струн об успешном соединении квантовой механики и общей теории относительности основывается на множестве вычислений, а также на убедительных результатах, описанных в главе 9.

Классическая механика: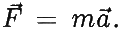

Электромагнетизм: d * F = * J; dF = 0. Квантовая механика:

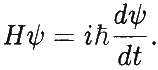
Общая теория относительности:

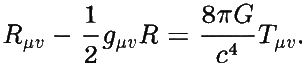
Я имею в виду постоянную тонкой структуры, α = e 2/ ħc, численное значение которой (при характерных энергиях электромагнитных процессов) примерно равно 1/137, что приближённо составляет 0,0073.

Согласно Виттену, когда константа связи в теории струн типа I становится большой, эта теория преобразуется в O-гетеротическую теорию с малой константой связи, и наоборот; теория типа IIB с большой константой связи преобразуется в себя, в теорию типа IIB, но с малой константой связи. В случае E-гетеротической и теории типа IIA ситуация более тонкая (более подробно см.: «Элегантная Вселенная», глава 12), но общая картина такова, что все пять теорий являются участниками целой сети взаимосвязей.

Для подготовленного читателя отметим, что особенность струн — одномерных объектов — состоит в том, что описывающая их движение физика основана на некоторой бесконечномерной группе симметрии. Так как при движении струна заметает двумерную поверхность, то струнный функционал действия, на основе которого выводятся уравнения движения, определяет двумерную квантовую теорию поля. Классически, такие двумерные действия являются конформно-инвариантными (инвариантными относительно сохраняющих углы растяжений двумерной поверхности), и при наложении некоторых ограничений (таких как число измерений пространства-времени, в котором движется струна) конформная симметрия может сохраняться на квантовом уровне. Конформная группа преобразований симметрии бесконечномерная и это существенно для математической согласованности пертурбативного квантового анализа движущейся струны. Например, бесконечное число возбуждений движущейся струны, которые иначе имели бы отрицательную норму (возникающую из отрицательного знака временной компоненты пространственно-временной метрики), может быть устранено с помощью преобразований «вращения» из бесконечномерной группы симметрии. Более подробно можно прочитать в книге: М. Green, J. Schwarz, and Е. Witten, «Superstring Theory». Vol. 1. Cambridge: Cambridge University Press, 1988.

Подобно истории многих открытий, заслуживают славы те, чьи идеи легли в основу, и те, кто указали на их важность. Большую роль в открытии бран в теории струн сыграли Майкл Дафф, Пол Хов, Такео Иннами, Келлог Стелле, Эрик Бергшофф, Эргин Жегин, Пол Таунсенд, Крис Халл, Крис Поп, Джон Шварц, Ашок Сен, Эндрю Строминджер, Куртис Калан, Джо Польчински, Петр Хоржава, Джин Дай, Роберт Лей, Герман Николаи и Бернард Девитт.

Внимательный читатель может сказать, что в инфляционной мультивселенной время также было вплетено фундаментальным способом, потому что, в конце концов, граница нашего пузырька служит отметкой начала времени в нашей Вселенной; за пределами нашего пузырька означает за пределами нашего времени. Это безусловно так, но здесь идея носит более общий характер — все обсуждавшиеся до сих пор мультивселенные были основаны на анализе, сфокусированном на процессах, происходящих в пространстве. В обсуждаемой мультивселенной главную роль с самого начала играет время.

Александр Фридман, «Мир как пространство и время», 1923.

Отметим как интересную деталь, что авторы циклической модели с бранами нашли вполне утилитарное применение тёмной энергии (тёмная энергия будет подробно обсуждаться в главе 6). В последнюю фазу каждого цикла присутствие тёмной энергии в мирах на бранах гарантирует согласие с современными наблюдениями ускоряющегося расширения; в свою очередь, это ускоряющееся расширение разбавляет плотность энтропии, что даёт начало следующему космологическому циклу.

Потоки с большими значениями также приводят к дестабилизации заданной формы Калаби–Яу. То есть потоки стремятся заставить форму Калаби–Яу увеличиваться в размерах, что сразу приводит к противоречию с критерием малости дополнительных измерений.

George Gamow, «My World Line». New York: Viking Adult, 1970; J. C. Pecker, Letter to the Editor, «Physics Today». May 1990, p. 117.

Albert Einstein, «The Meaning of Relativity». Princeton: Princeton University Press, 2004, p. 127. Отметим, что вместо принятого сейчас названия «космологическая постоянная» Эйнштейн использовал термин «космологический член»; в процитированном тексте я воспользовался этой заменой для наглядности.

«The Collected Papers of Albert Einstein», edited by Robert Schulmann et al. Princeton: Princeton University Press, 1998, p. 316.

Конечно же, некоторые вещи действительно изменяются. Как отмечалось в примечаниях к главе 3, у самих галактик есть небольшие скорости, сверх скорости пространственного расширения. На космологическом масштабе времени такое дополнительное движение может изменить взаимное расположение; оно также может привести к разным интересным астрофизическим событиям, таким как столкновение и слияние галактик. Однако для объяснения космических расстояний эти усложнения можно благополучно проигнорировать.

Есть одно усложнение, которое не влияет на основную идею, но которое начинает играть существенную роль при детальном научном анализе. При движении фотонов от сверхновой звезды к нам, плотность числа фотонов рассеивается описанным выше способом. Однако есть и другая причина для уменьшения. В следующем разделе будет рассказано, что растяжение пространства заставляет растягиваться длины волн фотонов, вследствие чего их энергии падают — эффект, называемый красным смещением. Астрономы используют данные по красному смещению для установления размера Вселенной в момент испускания этих фотонов — важный шаг в определении того, как расширение пространства меняется с течением времени. Но растяжение фотонов — уменьшение их энергии — проявляет себя ещё и другим способом: удалённый источник тускнеет. Поэтому для правильного определения расстояния до сверхновой путём сравнения видимой и собственной яркости астрономы должны учитывать не только рассеивание плотности числа фотонов (как описано в основном тексте), но дополнительно также и уменьшение энергии, вызванное красным смещением. (Если быть более точным, то дополнительный фактор уменьшения следует применить дважды; второй фактор красного смещения описывает степень растяжения длины фотона из-за космического расширения в момент приёма.)

В определённом смысле и второй вариант ответа на то, какое расстояние измеряется, также может считаться правильным. В примере раздувающейся поверхности Земли, города Нью-Йорк, Остин и Лос-Анджелес удаляются друг от друга, но их географическое положение на Земле остаётся при этом неизменным. Города удаляются друг от друга, потому что поверхность Земли раздувается, а не потому, что их выкапывают гигантским ковшом, кладут на прицеп и перевозят на новое место. Аналогично, хотя галактики из-за космического расширения разлетаются, их положение в пространстве остаётся неизменным. Представим себе, что галактики — это блёстки на космической ткани. Если ткань растягивать, блёстки начинают разъезжаться, но каждая из них остаётся пришитой к тому же самому месту, что и ранее. Поэтому если на первый взгляд второй и третий варианты ответа и кажутся разными — во втором речь идёт о расстоянии между нами и положением удалённой галактики миллиарды лет назад, когда сверхновая излучила свет, дошедший до нас сейчас, а в третьем рассматривается расстояние в данный момент между нами и текущим положением галактики, — на самом деле это не так. Положение удалённой галактики в пространстве оставалось неизменным как в настоящий момент, так и в течение миллиардов лет. Только движение через пространство, а не свободный дрейф по волнам пространственного расширения может изменить её положение. В этом смысле второй и третий ответы действительно одинаковы.

Поясним подготовленному читателю, как вычислить расстояние — сейчас, в момент времени t наст, — которое свет прошёл с момента излучения во время t изл. Мы будем рассматривать модель, в которой пространственная часть пространства-времени является плоской, и поэтому метрика может быть записана в виде

ds 2 = c 2 dt 2 − a 2(t) dx 2,

где a (t) — это масштабный фактор Вселенной в момент времени t, а c — скорость света. Используемые координаты называются сопутствующими. На образном языке этой главы их можно рассматривать как координаты, соответствующие точкам на статичной карте, а масштабный фактор даёт информацию, приведённую в легенде карты.

Траектории светового луча характеризуется тем, что ds 2 = 0 (это эквивалентно тому, что скорость света всегда равна c), откуда следует, что

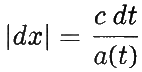
или, выбирая конечный интервал времени между t изл и t наст:

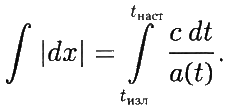
Левая часть этого уравнения задаёт расстояние, пройденное светом по статичной карте от момента излучения до настоящего момента. Чтобы перевести это в расстояние в реальном пространстве, необходимо перемасштабировать формулу с учётом современного масштабного фактора; поэтому полное расстояние, проходимое светом, будет равно

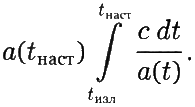
Если пространство не расширяется, полное пройденное расстояние будет

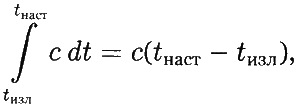
как и ожидалось. Таким образом, при вычислении расстояния, пройденного в расширяющейся Вселенной, мы видим, что каждый участок траектории светового луча умножается на фактор a (t наст)/ a (t), который характеризует то, как на настоящий момент увеличился участок траектории с того момента, как через него прошёл свет.

Более точно примерно 7,12 × 10−30 грамма/кубический сантиметр.

Пересчёт составляет 7,12 × 10−30 грамма/кубический сантиметр = (7,12 × 10−30 грамма/кубический сантиметр) × (4,6 × 104 планковская масса/грамм) × (1,62 × 10−33 сантиметр/планковская длина)3 = 1,38 × 10−123 планковская масса/кубический планковский объём.

Гравитационное отталкивание при инфляции является кратким и интенсивным. Это объясняется огромной энергией и отрицательным давлением, обусловленными полем инфлатона. Однако если изменить форму кривой потенциальной энергии квантового поля, то количество энергии уменьшится и отрицательное давление снизится, что снизит интенсивность ускоренного расширения. Кроме того, при подходящей модификации кривой потенциальной энергии можно продлить период ускоренного расширения. А такой менее интенсивный и более продолжительный период ускоренного расширения — именно то, что требуется для объяснения данных по сверхновым. Однако за более чем десять лет с момента первого наблюдения ускоренного расширения, наиболее убедительным объяснением остаётся наличие у космологической постоянной небольшого отличного от нуля значения.

Вдумчивый читатель заметит, что каждая флуктуация даёт вклад в энергию, обратно пропорциональный её длине волны, откуда следует, что сумма по всем возможным длинам волн приводит к бесконечной энергии.

Заметим, что сокращение происходит благодаря тому, что суперсимметрия спаривает бозоны (частицы с целым спином) и фермионы (частицы с полуцелым (нечётным) спином). Так как бозоны описываются коммутирующими переменными, а фермионы описываются антикоммутирующими переменными, это приводит к противоположным знакам их квантовых флуктуаций.

Хотя утверждение о том, что изменения физических свойств нашей Вселенной не будут благоприятствовать жизни в привычном виде, широко признано научной общественностью, некоторые учёные полагают, что диапазон значений, совместимых с жизнью, может быть шире, чем принято думать. Эти вопросы широко обсуждались в литературе. См., например: John Barrow and Frank Tipler, «The Anthropic Cosmological Principle». New York: Oxford University Press, 1986; John Barrow, «The Constants of Nature». New York: Pantheon Books, 2003; Paul Davies, «Th

Date: 2015-09-05; view: 284; Нарушение авторских прав