По закону Архимеда

Архимед (287–212 до н. э.), один из самых великих математиков древности, родился в Сиракузах, греческой колонии на острове Сицилия. Отцом его был Фидий, придворный астроном правителя города царя Гиерона II, дожившего до 90 лет и сумевшего уберечь свою родину от завоевания Римом и Карфагеном.

Архимед

Отец дал сыну отличное образование, включая первоначальные знания по астрономии и математике. А потом Архимед, как и многие другие древнегреческие ученые, учился в Александрии, где правители Египта в то время собрали лучших ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку. Есть данные, что Архимед общался и даже был дружен с Кононом Самосским (280–220 до н. э.), служившим придворным астрономом у правителя Птолемея III. Считается, что именно под его влиянием Архимед начал серьезно заниматься математикой.

После учебы в Александрии Архимед вновь вернулся в Сиракузы, где унаследовал должность своего отца.

Основные научные работы Архимеда касались всевозможных практических применений математики, физики, гидростатики и механики. В частности, в сочинении «Параболы квадратуры» он обосновал метод расчета площади параболического сегмента. Удивительно, но сделано это было за 2000 лет до открытия интегрального исчисления. В своем труде «Об измерении круга» Архимед впервые предложил математический способ вычисления числа «пи» (отношения длины окружности к длине ее диаметра) и доказал, что оно одинаково для любого круга.

Для этого Архимед вписывал в окружность и описывал около нее правильные многоугольники. Принимая диаметр окружности за единицу, он рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. На примере правильного 96‑угольника Архимеду удалось получить следующие значения числа «пи»:

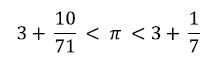
Как видим, согласно Архимеду, значение числа «пи» находится в диапазоне от 3,1408 до 3,1428. В настоящее время вычислено огромное количество знаков после запятой, и число «пи» признано равным 3,14159265…

А еще мы до сих пор пользуемся придуманной Архимедом системой наименования целых чисел.

Важнейшим достижением Архимеда являются теоретические изыскания и практические работы в области механики. Фактически Архимед является создателем механики как науки, изучающей законы движения, покоя и равновесия тел. В течение многих веков фундаментом механики была теория рычага, изложенная Архимедом в сочинении «О равновесии плоских фигур». В основе этой теории лежат следующие постулаты:

...

«Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине.

Если при равновесии тяжестей на каких‑нибудь длинах к одной из тяжестей будет что‑нибудь прибавлено, то они не будут уравновешиваться, но перевесит та тяжесть, к которой было прибавлено.

Точно так же, если от одной из тяжестей будет отнято что‑нибудь, то они не будут уравновешиваться, но перевесит та тяжесть, от которой не было отнято».

Даже по формулировкам видно, что эти постулаты были проверены на опыте, а не придуманы исключительно «за письменным столом». Основываясь на них, Архимед сделал следующие утверждения:

...

«Соизмеримые величины уравновешиваются на длинах, которые будут обратно пропорциональны тяжестям.

Если величины будут несоизмеримы, то они точно так же уравновесятся на длинах, которые обратно пропорциональны этим величинам».

В этих словах содержится первая точная формулировка закона рычага. Кроме того, в книге «О равновесии плоских фигур» содержатся примеры определения центров тяжести треугольника, параллелограмма, трапеции и других фигур. Кстати сказать, Архимед описывал центр тяжести следующим образом:

...

«Центром тяжести каждого тела является некоторая расположенная внутри его точка – такая, что если за нее мысленно подвесить тело, то оно остается в покое и сохраняет первоначальное положение».

Учение о гидростатике Архимед развил в своем труде «О плавающих телах», в котором было сказано:

...

«Предположим, что жидкость имеет такую природу, что из ее частиц, расположенных на одинаковом уровне и прилежащих друг к другу, менее сдавленные выталкиваются более сдавленными, и что каждая из ее частиц сдавливается жидкостью, находящейся над ней по отвесу, если только жидкость не заключена в каком‑нибудь сосуде и не сдавливается еще чем‑нибудь другим».

Основываясь на этом, Архимед математически доказал, что:

...

«Тела, равнотяжелые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости, и не будут двигаться вниз.

Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, не погружается целиком, но некоторая часть его остается над поверхностью жидкости.

Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погруженной [части тела], имел вес, равный весу всего тела.

Тела, более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела.

Тела, более тяжелые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела».

Последнее утверждение фактически и содержит общеизвестный закон Архимеда, важный закон гидростатики, согласно которому каждое тело, погруженное в жидкость, теряет столько своего веса, сколько весит вытесненная им жидкость (на тело, погруженное в жидкость, действует сила, равная весу вытесненной им жидкости).

Отметим, что знаменитое восклицание «Эврика!» («Я нашел!») относится к первому практическому применению этого самого закона Архимеда.

Согласно легенде, однажды к Архимеду обратился недоверчивый правитель Сиракуз, подозревавший своего ювелира в обмане. Он попросил проверить, соответствует ли вес изготовленной для него золотой короны весу отпущенного им на нее золота.

Рассказ об этом приведен у древнеримского автора второй половины I века до н. э. Марка Витрувия Поллиона в его трактате «Десять книг об архитектуре»:

...

«Исходя из своего открытия, он, говорят, сделал два слитка, каждый такого же веса, какого была корона, – один из золота, другой из серебра. Сделав это, он наполнил водой сосуд до самых краев и опустил в него серебряный слиток, и вот, какой объем слитка был погружен в сосуд, соответственное ему количество вытекло воды. Вынув слиток, он долил в сосуд такое количество воды, на какое количество стало там ее меньше, отмеряя вливаемую воду секстарием [1], чтобы, как и прежде, сосуд был наполнен водой до самых краев. Так отсюда он нашел, какой вес серебра соответствует какому определенному количеству воды.

Произведя такое исследование, он после этого таким же образом опустил золотой слиток в полный сосуд. Потом, вынув его и добавив той же мерой вылившееся количество воды, нашел на основании меньшего количества секстариев воды, насколько меньший объем занимает слиток золота по сравнению с одинаково с ним весящим слитком серебра. После этого, наполнив сосуд и опустив в ту же воду корону, нашел, что при погружении короны вытекло больше воды, чем при погружении золотой массы одинакового с ней веса; и таким образом на основании того заключения, что короной вытеснялось большее количество воды, чем золотым слитком, он вскрыл примесь в золоте серебра и обнаружил явное воровство поставщика».

Итак, Архимед сделал два слитка: один из золота, другой из серебра, и каждый – такого же веса, что и корона. Затем он поочередно положил их в сосуд с водой, отметив, насколько поднялся ее уровень. Опустив в сосуд корону, Архимед установил, что ее объем превышает объем золотого слитка, а это значило, что корона изготовлена не из чистого золота, а из сплава золота с серебром.

Я. Г. Дорфман в своей «Всемирной истории физики» отмечает:

...

«Это выдающееся открытие Архимеда знаменует собой первое в истории применение физического измерительного метода к контролю и анализу химического состава без нарушения целостности изделия. Огромное практическое значение этого открытия в эпоху, когда еще никаких других методов подобного рода не было, естественно, привлекло к себе всеобщее внимание и стало предметом дальнейших исследований и практических использований на протяжении многих последующих веков».

Но Архимед не ограничился описанным выше достаточно примитивным экспериментом, а перешел к более точному количественному измерению. По словам жившего в первой половине XII века среднеазиатского физика, астронома и математика Ал‑Хазини, ссылавшегося на не дошедший до нас трактат грека Менелая Александрийского, Архимед «изобрел механическое приспособление, которое, благодаря своему тонкому устройству, позволило ему определить, сколько золота и сколько серебра содержится в короне, не нарушая ее формы».

Ал‑Хазини привел схему этих «весов Архимеда». На них имелся подвижный груз, с помощью которого можно было, сравнивая веса упомянутых слитков, определять численное отношение удельных весов золота и серебра. А это, в свою очередь, позволяло установить относительное количество золота и серебра в короне.

Потом, основываясь на принципах Архимеда, грек Синезий из Кирены, живший в IV веке, изобрел гидроскоп – прибор для определения удельного веса жидкостей. Этот прибор, изготовленный из бронзы, имел насечки, и по ним можно было находить точные значения, используя специальные таблицы удельных весов различных жидкостей. К сожалению, подобные таблицы до наших дней не сохранились.

Наряду с фундаментальной наукой, Архимед много времени уделял практике. Он по праву считался одним из крупнейших инженеров своего времени.

Страстно увлеченный механикой, Архимед создал и проверил теорию пяти простых механизмов: рычага, клина, блока, бесконечного винта (он используется в современной мясорубке) и лебедки.

Архимед говорил: «Дайте мне точку опоры, и я сдвину Землю». Кстати сказать, ученые потом подсчитали, что теоретически это возможно, но для этого надо иметь рычаг, у которого один отрезок длиннее другого в 1023 раз.

В древности Архимеду приписывали около 40 открытий в области практической механики. Из того, что описано его биографами, известно, что на основе бесконечного винта Архимед изобрел машину для поливки полей (так называемую «улитку»), устройство для откачки воды из трюмов и шахт и, наконец, пришел к изобретению болта, сконструировав его из винта и гайки.

Но наиболее успешно Архимед придумывал конструкции военных машин. И это понятно. Могущественные соседи – Рим и Карфаген – прилагали немало усилий для того, чтобы подчинить себе Сиракузы. В свою очередь, царь Гиерон и его преемники делали все, чтобы сохранить независимость, поэтому в оборонительных планах Сиракуз военная техника занимала особое место.

Известно, что под руководством Архимеда сиракузцы построили множество устройств: это были и мощные метательные машины, и подъемные механизмы для переворачивания атакующих кораблей противника, и т. д. В основе всех этих конструкций лежал рычаг, позволявший поднимать большие тяжести, затрачивая относительно небольшие усилия. Отсюда, кстати, и пошло название «механика», что в переводе с греческого означает «искусство построения машин».

В очередной раз римляне, под командованием полководца Марка Клавдия Марцелла, осаждали Сиракузы во время второй Пунической войны. При этом Архимед был душой сопротивления. Он сконструировал несколько боевых машин, которые позволили горожанам в течение трех лет отражать атаки превосходящего в живой силе противника.

К сожалению, даже знания Архимеда не смогли спасти его родину от печальной участи: в 212 году до н. э. римляне вторглись в Сиракузы и подвергли город грабежу. При этом сам Архимед погиб: его зарубил мечом римский солдат. Согласно легенде, произошло это в тот момент, когда старик ученый был поглощен поисками решения очередной технической задачи. Он сидел на полу, посыпанном песком, на котором были начерчены какие‑то замысловатые геометрические фигуры. Когда римлянин подбежал к нему, Архимед якобы встретил его словами: «Только не трогай моих фигур!».

Смерть Архимеда

Информация о жизни и смерти Архимеда известна нам из сочинений античных философов и историков Полибия, Тита Ливия, Цицерона, Плутарха и других. Но никто из них, как известно, не был современником Архимеда, поэтому достоверность их сведений оценить не всегда представляется возможным. Тем не менее, многие эпизоды явно имеют мифический оттенок. Возьмем для примера так называемые «зажигательные зеркала» Архимеда. Считается, что великий сиракузец хорошо знал о зажигательном действии вогнутых зеркал. Следовательно, чисто теоретически он вполне мог использовать эти зеркала в борьбе с римским флотом, поджигая корабли сфокусированными солнечными лучами.

«Зажигательное зеркало» Архимеда

Тем не менее, в дошедших до нас описаниях штурма города нет никаких упоминаний о сожжении римских кораблей. Эта легенда появилась позднее. Например, четыре века спустя вопрос о «зажигательных зеркалах» разбирал византийский математик и архитектор Анфимий, который в сочинении «О чудесных механизмах» попытался дать реконструкцию изобретений Архимеда. При этом «о зеркалах божественного Архимеда» он писал следующее:

...

«При помощи многих плоских зеркал можно отразить в одну точку такое количество солнечного света, что его объединенное действие вызовет загорание».

Анфимию вторит и византиец Евстахий Солунский. В его «Комментариях к Илиаде» читаем:

...

«Архимед при помощи правил катоптрики [2] сжег римский флот на расстоянии полета стрелы».

А вот византийский историк XII века Иоанн Зонара в своих «Анналах» рассказывает:

...

«Этот геометр, собрав солнечные лучи на зеркале, с помощью этих лучей, собранных и отраженных затем толщиной и гладкостью зеркала, воспламенил воздух и разжег большое пламя, которое он затем направил на корабли, входившие в сферу его действия. Корабли были все обращены в пепел».

В своей «Истории» другой византиец конца XII века Цеци уточняет: Архимед действовал «шестиугольным зеркалом, составленным из небольших четырехугольных зеркал, которые можно было двигать при помощи шарниров и металлических планок».

Долгое время этому оставалось только верить. Но вот в XVII веке немецкий астроном Иоганн Кеплер (1571–1630) и французский математик Рене Декарт (1596–1650) обосновали невозможность создания таких фантастических зеркал.

С другой стороны, в 1747 году знаменитый французский естествоиспытатель Жорж‑ Луи де Бюффон (1707–1788) в своем труде «Изобретение зеркал для воспламенения предметов на больших расстояниях» сообщил, что произвел опыты и соорудил составное зеркало, которое подожгло дерево на расстоянии 50 метров. Этими опытами он подтвердил тот факт, что Архимед вполне мог создать грозное орудие – мощный гелиоконцентратор или «солнечный лазер». К сожалению, это могло быть лишь теоретически, ибо во времена Архимеда еще не существовало зеркал такого качества, с которыми проводились опыты де Бюффона.

После этого некоторые итальянские историки высказали предположение, что зеркала Архимеда существовали, но были предназначены не для поджога, а для наведения на цель. Они якобы били в глаза римлянам отраженным солнечным светом и «скрывали» от них полет зажигающих стрел сиракузцев.

Естественно, это всего лишь предположение, и стопроцентно доказать ничего невозможно. Впрочем, и того, что реально дошло до нас, совершенно достаточно, чтобы обессмертить память об Архимеде.

Недаром древнеримский политик и философ Марк Туллий Цицерон, величайший из ораторов древности, дал Архимеду следующую оценку:

...

«Этот сицилиец обладал гением, которого, казалось бы, человеческая природа не может достигнуть».

Date: 2015-09-05; view: 704; Нарушение авторских прав