Простейшие случаи движения микрочастиц

· Одномерное временное уравнение Шредингера

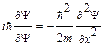
где i— мнимая единица (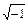); m— масса частицы; ψ (х, t)— волновая функция, описывающая состояние частицы.

Волновая функция, описывающая одномерное движение свобод­ной частицы,

W(x,t) = Aexp 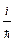(px – Et),

где А — амплитуда волны де Бройля; р — импульс частицы; Е — энергия частицы.

Одномерное уравнение Шредингера для стационарных состояний

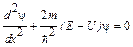
где Е — полная энергия частицы; U (x) - потенциальная энергия;

ψ (x) — координатная (или амплитудная) часть волновой функции

Для случая трех измерений ψ(x, y, z,) уравнение Шредингера

или в операторной форме

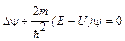, где 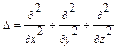— оператор Лапласа

При решении уравнения Шредингера следует иметь в виду стан­дартные условия которым должна удовлетворять волновая функция: конечность (во всем пространстве), однозначность, непроч­ность самой ψ - функции и ее первой производной.

· Вероятность d W обнаружить частицу в интервале от х до x + dx (в одномерном случае) выражается формулой

dW = [ ψ(x) ] ² d x

где [ y (x) ]²— плотность вероятности.

Вероятность W обнаружить частицу в интервале от х ₁ до х ₂находится интегрированием d W в указанных пределах

W= 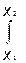[ y(x) ²­ d x

· Собственное значение энергии Е_n частицы, находящейся на n-м энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенициальеом ящике, определяется формулой

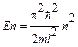(n = 1, 2, 3, …)

где l — ширина потенциального ящика.

Соответствующая этой энергии собственная волновая функция имеет вид

y_n (x) = 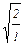sin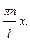

· Коэффициент преломления п воли де Бройля на границе низкого потенциального барьера бесконечной ширины * (рис. 46.1)

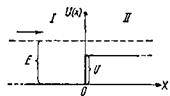
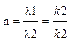где l₁ и l₂— длины волн де Бройля в областях I и II (частица дви­жется из области I во II ); k ₁— k ₂ — соответствующие значения волновых чисел.

· Коэффициенты отражения r и пропускания t волн де Бройля через низкий (U < E) потенциальный барь­ер бесконечной ширины

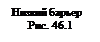r =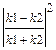

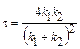
где k₁ и k ₂ — волновые числа волн де Бройля в областях I и II.

· Коэффициент прозрачности D прямоугольного потенциаль­ного барьера конечной ширины

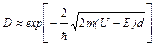, где U — высота потенциального барьера; Е — энергия частицы; d— ширина барьера.

Date: 2015-09-05; view: 557; Нарушение авторских прав