
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Характеристики синхронных машин
|
|
10.20.1. Основные характеристики
Рабочие свойства машины определяются ее характеристиками. Для генераторов основными характеристиками являются внешняя, регулировочная, U -образная и угловая, для двигателей — рабочие, U –образная и угловая. Для построения всех указанных характеристик используют векторные диаграммы [6].
Регулировочная характеристика генератора представляет собой зависимость 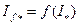 при
при  =const и
=const и 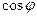 =const (рис. 10.39). Для построения этой характеристики задают ряд значений тока якоря
=const (рис. 10.39). Для построения этой характеристики задают ряд значений тока якоря 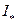 в пределах от 0 до 1 и при одних и тех же значениях
в пределах от 0 до 1 и при одних и тех же значениях  и
и 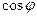 строят векторные диаграммы, из которых находят ток возбуждения. Ток возбуждения при
строят векторные диаграммы, из которых находят ток возбуждения. Ток возбуждения при 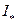 =0 определяют из характеристики холостого хода по заданному напряжению. Для регулировочной характеристики при
=0 определяют из характеристики холостого хода по заданному напряжению. Для регулировочной характеристики при  =1=const и
=1=const и 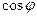 =
= 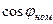 =const ток возбуждения, соответствующий номинальному току якоря, можно определить по векторной диаграмме, построенной раньше для нахождения МДС обмотки возбуждения (см. § 10.14). Эта МДС в относительных единицах равна току возбуждения
=const ток возбуждения, соответствующий номинальному току якоря, можно определить по векторной диаграмме, построенной раньше для нахождения МДС обмотки возбуждения (см. § 10.14). Эта МДС в относительных единицах равна току возбуждения 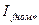 .
.
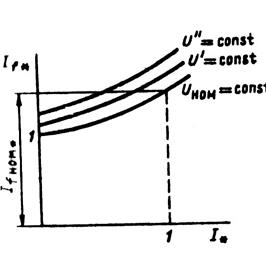
Рис. 10.39. Регулировочные характеристики
Внешняя характеристика 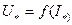 при
при 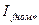 =const и
=const и 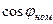 =const (рис. 10.40) определяет зависимость напряжения генератора от его нагрузки. Исходная точка этой характеристики имеет координаты
=const (рис. 10.40) определяет зависимость напряжения генератора от его нагрузки. Исходная точка этой характеристики имеет координаты  =1 и
=1 и 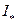 =1. При токе
=1. При токе 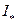 =0 напряжение
=0 напряжение  =
= 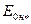 берут из векторной диаграммы, построенной для номинального режима машины. Промежуточные точки характеристики можно найти, построив ряд регулировочных характеристик при различных значениях напряжения
берут из векторной диаграммы, построенной для номинального режима машины. Промежуточные точки характеристики можно найти, построив ряд регулировочных характеристик при различных значениях напряжения 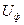 . Напряжения
. Напряжения  , при которых строят регулировочные характеристики, берут в пределах от
, при которых строят регулировочные характеристики, берут в пределах от 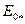 до 1, а
до 1, а 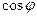 =
= 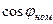 . Точки пересечения регулировочных характеристик с прямой, проведенной параллельно оси абсцисс, при
. Точки пересечения регулировочных характеристик с прямой, проведенной параллельно оси абсцисс, при 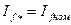 дают искомые точки внешней характеристики.
дают искомые точки внешней характеристики.
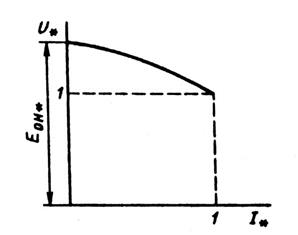
Рис. 10.40. Внешняя характеристика
U-образные характеристики 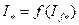 при
при 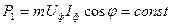 (рис. 10.41) можно получить путем построения ряда векторных диаграмм при
(рис. 10.41) можно получить путем построения ряда векторных диаграмм при 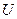 =1=const и
=1=const и 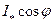 =const (рис. 10.42). Из построенных векторных диаграмм для каждого значения тока
=const (рис. 10.42). Из построенных векторных диаграмм для каждого значения тока 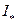 определяют ток возбуждения
определяют ток возбуждения 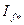 .
.
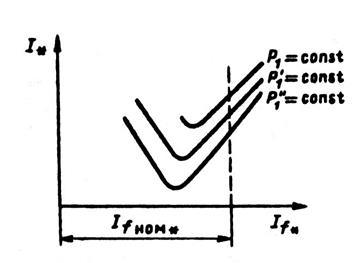
Рис. 10.41. U — образные характеристики

Рис. 10.42. К построению U — образных характеристик
Угловые характеристики дают зависимость активной мощности от 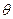 (угла нагрузки):
(угла нагрузки): 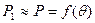 при
при  = 1 и
= 1 и 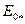 =const. Угол
=const. Угол 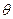 является углом между осями полюсов и результирующего магнитного поля или между векторами ЭДС
является углом между осями полюсов и результирующего магнитного поля или между векторами ЭДС 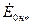 и напряжения
и напряжения 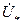 . Построение угловых характеристик с учетом насыщения машины связано с большими трудностями. Ниже приведен расчет этой характеристики без учета насыщения. Параметры в этом случае принимают постоянными, равными их значению для ненасыщенной машины, а
. Построение угловых характеристик с учетом насыщения машины связано с большими трудностями. Ниже приведен расчет этой характеристики без учета насыщения. Параметры в этом случае принимают постоянными, равными их значению для ненасыщенной машины, а 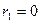 .
.
Характеристику при  = l в относительных единицах строят по уравнению
= l в относительных единицах строят по уравнению
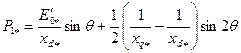 . (10.174)
. (10.174)
Электродвижущую силу 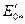 определяют по продолжению прямолинейной части характеристики холостого хода при токе возбуждения
определяют по продолжению прямолинейной части характеристики холостого хода при токе возбуждения 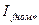 . При построении характеристики
. При построении характеристики 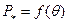 угол
угол 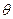 изменяется в пределах от 0 до
изменяется в пределах от 0 до 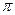 .
.
По угловой характеристике определяют статическую перегружаемость машины, равную отношению 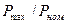 . Номинальная мощность
. Номинальная мощность 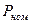 в относительных единицах равна
в относительных единицах равна 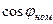 . Если пренебречь активным сопротивлением (что возможно для машин средней и большой мощности), то можно принять
. Если пренебречь активным сопротивлением (что возможно для машин средней и большой мощности), то можно принять
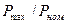 =
= 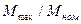 , (10.175)
, (10.175)
где 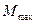 и
и  — максимальный и номинальный моменты.
— максимальный и номинальный моменты.
Статическую перегружаемость можно также рассчитать по формуле
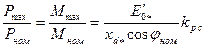 . (10.176)
. (10.176)
Коэффициент 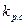 учитывает реактивные составляющие мощности и момента, обусловленные неодинаковыми индуктивными сопротивлениями
учитывает реактивные составляющие мощности и момента, обусловленные неодинаковыми индуктивными сопротивлениями  и
и 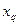 . Он принимается по рис. 10.43 в зависимости от отношения
. Он принимается по рис. 10.43 в зависимости от отношения 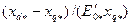 .
.
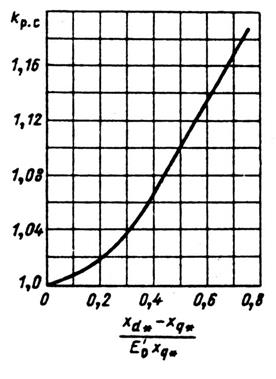
Рис. 10.43. К определению коэффициента 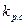
Как уже отмечалось ранее, статическая перегружаемость синхронных двигателей общего назначения должна быть не ниже 1,65.
Для синхронных двигателей U -образные и угловые характеристики строят так же, как и для генераторов, с использованием соответствующих векторных диаграмм.
Рабочие характеристики двигателей, т. е. зависимости 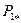 ,
, 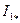 ,
, 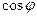 ,
, 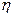 ,
, 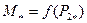 , при
, при  =1=const и
=1=const и 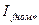 =const могут быть получены по U -образным характеристикам. Для этого необходимо построить несколько U -образных характеристик при различных значениях
=const могут быть получены по U -образным характеристикам. Для этого необходимо построить несколько U -образных характеристик при различных значениях 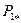 =const и
=const и  =1=const. По этим характеристикам при
=1=const. По этим характеристикам при 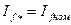 находят ток I при данном значении мощности
находят ток I при данном значении мощности 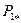 и
и 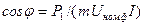 . Затем определяют мощность на валу:
. Затем определяют мощность на валу: 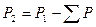 (
(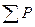 — потери в машине для данного режима работы),
— потери в машине для данного режима работы), 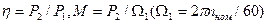 .
.
10.20.2. Токи короткого замыкания
При расчете механических усилий, воздействующих на лобовые части обмотки статора и на их бандажи, исходят из наибольшего мгновенного значения тока трехфазного короткого замыкания на выводах машины при данном значении возбуждения. Этот ток называется ударным током короткого замыкания.
Согласно ГОСТ 183 синхронная машина должна выдерживать ударный ток короткого замыкания при напряжении холостого хода, равном 105% номинального:
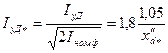 . (10.177)
. (10.177)
Коэффициент 1,8 учитывает затухание апериодической составляющей тока короткого замыкания.
Для машин без демпферной обмотки в (10.177) вместо 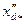 следует подставить
следует подставить 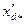 .
.
Практический интерес представляют кратности установившихся токов короткого замыкания. Под этим понимают отношение установившегося тока короткого замыкания к номинальному току обмотки якоря.
Кратность при возбуждении холостого хода, т. е. при возбуждении, которое при номинальной частоте вращения и разомкнутой обмотке якоря дает на выводах машины номинальное напряжение, обозначают ОКЗ (отношение короткого замыкания):
ОКЗ = 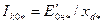 , (10.178)
, (10.178)
где 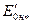 — ЭДС, определяемая по продолжению прямолинейной части характеристики холостого хода при
— ЭДС, определяемая по продолжению прямолинейной части характеристики холостого хода при 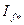 =1.
=1.
Кратность при номинальном токе возбуждения
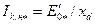 . (10.179)
. (10.179)
10.20.3. Пусковые характеристики
Основным методом пуска синхронных двигателей в настоящее время является асинхронный пуск. Для этого в полюсах ротора размещается пусковая обмотка по типу короткозамкнутой обмотки ротора асинхронного двигателя.
Оценку пусковых свойств двигателя производят по пусковым характеристикам, т. е. зависимостям тока в статоре и момента от скольжения 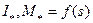 . Наибольший интерес на этих характеристиках представляют величины, соответствующие s =l: начальный пусковой ток
. Наибольший интерес на этих характеристиках представляют величины, соответствующие s =l: начальный пусковой ток 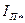 и начальный пусковой момент
и начальный пусковой момент 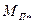 , а также момент при скольжении s =0,05 — входной момент в синхронизм
, а также момент при скольжении s =0,05 — входной момент в синхронизм 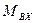 .
.
При расчете пусковых характеристик необходимо учитывать, что в отличие от ротора обычного асинхронного двигателя ротор синхронного явнополюсного двигателя имеет магнитную и электрическую несимметрии. Если условно подразделить пусковую обмотку на две части, то можно принять, что по продольной оси машины на роторе располагаются две обмотки, одной из которых является обмотка возбуждения, а другой — часть пусковой обмотки, представляющая ее эффект по продольной оси. По поперечной оси на роторе имеется только пусковая обмотка, представляющая ее эффект по поперечной оси. Необходимо также учитывать, что обмотка статора по продольной и поперечной осям имеет неодинаковые индуктивные сопротивления 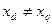 .
.
На основании сказанного полное сопротивление по продольной оси машины, которое зависит от скольжения s, будет равно:
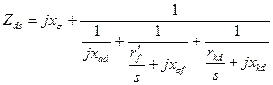 , (10.180)
, (10.180)
где 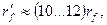 [
[ 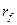 — по (10.135)].
— по (10.135)].
Полное сопротивление по поперечной оси
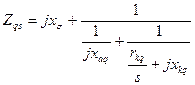 . (10.181)
. (10.181)
В приведенных формулах значения всех параметров принимают в относительных единицах (здесь и далее звездочка в обозначениях величин в относительных единицах опускается).
Вследствие магнитной и электрической несимметрий машины в статоре кроме тока I' основной частоты 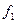 протекают токи I'' частоты 2 s— 1. Значения их могут быть найдены по следующим формулам:
протекают токи I'' частоты 2 s— 1. Значения их могут быть найдены по следующим формулам:
ток якоря частоты 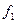
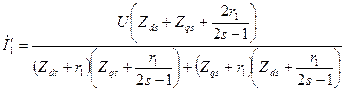 ; (10.182)
; (10.182)
ток якоря частоты 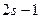
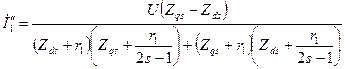 ; (10.183)
; (10.183)
действующее значение тока статора
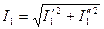 ; (10.184)
; (10.184)
момент вращения
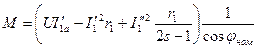 , (10.185)
, (10.185)
где 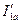 — активная составляющая тока
— активная составляющая тока 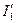 .
.
Последний член выражения в скобках соответствует моменту, создаваемому током 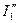 . При скольжениях s > 0,5 этот момент положительный, а при s < 0,5 — отрицательный, в результате чего в кривой
. При скольжениях s > 0,5 этот момент положительный, а при s < 0,5 — отрицательный, в результате чего в кривой  могут наблюдаться провалы. Из-за наличия провалов в кривой момента при разгоне двигатель может застрять на промежуточной скорости и не войти в синхронизм. Обычно для уменьшения провала в кривой момента обмотку ротора замыкают на добавочный резистор с сопротивлением, примерно в 10 раз большим сопротивления самой обмотки.
могут наблюдаться провалы. Из-за наличия провалов в кривой момента при разгоне двигатель может застрять на промежуточной скорости и не войти в синхронизм. Обычно для уменьшения провала в кривой момента обмотку ротора замыкают на добавочный резистор с сопротивлением, примерно в 10 раз большим сопротивления самой обмотки.
В этом случае при определении 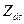 и
и 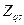 , как уже указывалось, сопротивление
, как уже указывалось, сопротивление 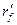 принимается равным (10-12)
принимается равным (10-12) 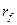 .
.
Расчет по приведенным формулам связан с большой вычислительной работой. Его можно упростить, если у машин средней и большой мощности пренебречь активным сопротивлением 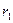 . Тогда получим
. Тогда получим
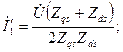
(10.186)
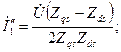
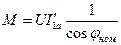 . (10.187)
. (10.187)
Погрешность такого расчета по сравнению с расчетом по (10.177) — (10.180) не превышает 4%.
Для построения пусковых характеристик задают ряд значений скольжения s в пределах от 1 до 0,05 и для каждого его значения определяют ток 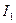 и М. Иногда можно ограничиться расчетом начального пускового и входного моментов и начального пускового тока.
и М. Иногда можно ограничиться расчетом начального пускового и входного моментов и начального пускового тока.
Промышленность выпускает двигатели со следующими значениями:
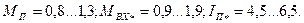
Пример расчета трехфазного синхронного двигателя
Проектное задание:
1. Номинальная мощность 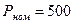 кВт.
кВт.
2. Номинальное напряжение (линейное) 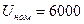 В.
В.
3. Номинальная частота вращения 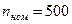 об/мин.
об/мин.
4. Частота 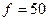 Гц.
Гц.
5. 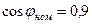 (опережающий).
(опережающий).
6. Кратность максимального момента 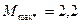 .
.
Режим работы — продолжительный. Конструкция — защищенная (IP11) с горизонтальным валом.
Номинальные величины
1. Номинальное фазное напряжение (предполагается, что обмотка статора соединена в звезду)
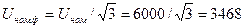 В.
В.
2. Номинальная полная мощность
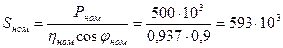 В·А
В·А
(по табл. 10.3, исходя из номинальных данных машины, определяем 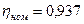 ).
).
3. Номинальный фазный ток
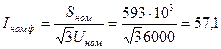 А.
А.
4. Число пар полюсов
 .
.
5. расчетная мощность
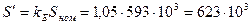 В·А.
В·А.
Размеры статора
6. По рис. 10.8 для 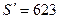 кВ·А при
кВ·А при 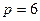 предварительно находим внутренний диаметр статора
предварительно находим внутренний диаметр статора  м.
м.
7. Внешний диаметр статора по (10.3)
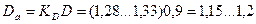 м.
м.
По табл. 10.7 ближайший нормализованный внешний диаметр статора 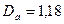 м (16-й габарит). Высота оси вращения
м (16-й габарит). Высота оси вращения 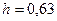 м.
м.
Поскольку найденный диаметр 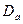 лежит в пределах, задаваемых коэффициентом
лежит в пределах, задаваемых коэффициентом 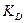 , то пересчет диаметра не производим.
, то пересчет диаметра не производим.
8. Полюсное деление по (10.4)
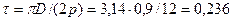 м.
м.
9. Расчетная длина статора. По рис. 10.9. для 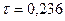 при
при 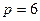 находим
находим 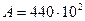 А/м,
А/м, 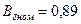 Тл. Задаемся
Тл. Задаемся 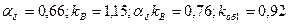 . По (10.5) определяем расчетную длину статора:
. По (10.5) определяем расчетную длину статора:
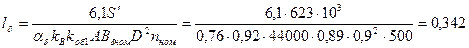 м.
м.
10. Находим 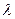 по (10.6):
по (10.6):
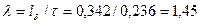 .
.
По рис. 10.11 устанавливаем, что найденное значение 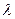 при
при 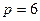 лежит в допустимых пределах, ограниченных кривыми.
лежит в допустимых пределах, ограниченных кривыми.
11. Действительная длина статора по (10.7)
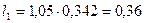 м.
м.
12. Число вентиляционных каналов по (10.8) при 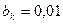 м.
м.
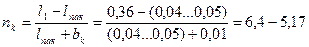 .
.
Принимаем 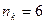 .
.
13. Длина пакета по (10.9)
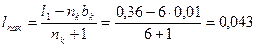 м.
м.
14. Суммарная длина пакетов магнитопровода по (10.10)
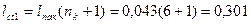 м.
м.
Зубцовая зона статора. Сегментировка
15. Число параллельных ветвей обмотки статора.
Так как 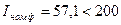 А, то выбираем
А, то выбираем 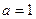 .
.
16. По рис. 10.13 (кривая 2) для 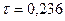 м находим
м находим 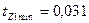 м;
м; 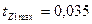 м.
м.
17. Максимальное число пазов (зубцов) магнитопровода статора
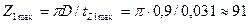 .
.
18. минимальное число пазов (зубцов) магнитопровода статора
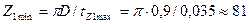 .
.
19. Число пазов магнитопровода статора.
Так как 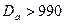 мм, то магнитопровод статора выполняется сегментированным. В диапазоне пазов
мм, то магнитопровод статора выполняется сегментированным. В диапазоне пазов 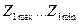 требованиям п. 1—4 § 10.6 удовлетворяет числа пазов
требованиям п. 1—4 § 10.6 удовлетворяет числа пазов 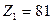 .
.
При этом
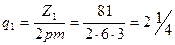 ;
; 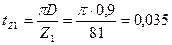 м
м
и
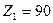
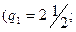
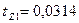 м
м 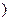 .
.
20. Расчет числа проводников в пазу 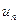 по (10.15), числа сегментов
по (10.15), числа сегментов 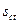 и хорды
и хорды 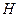 по (10.20), а также уточненной линейной нагрузки
по (10.20), а также уточненной линейной нагрузки 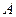 по (10.16) сводим в табл. 10.15.
по (10.16) сводим в табл. 10.15.
Наилучший результат дает вариант 3, который и принимаем для дальнейших расчетов.
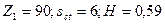 м (сегменты штампуются из листов 600
м (сегменты штампуются из листов 600 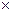 1500 мм);
1500 мм); 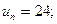
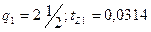 м;
м; 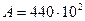 А/м.
А/м.
Таблица 10.15. Расчетные значения
| № варианта | Число пазов 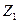
| Число сегментов 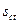
| Хорда 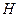 , м , м
| Число пазов в сегменте 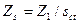
| Число пазов на полюс и фазу 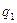
| Число параллельных ветвей 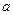
| Число проводников в пазу 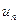
| Пазовое (зубцовое) деление 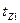 , м , м
| Линейная нагрузка 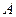 , А/м , А/м
|
| 81 = =3·3·3·3 | 0,402 | 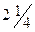
| 0,035 | ||||||
| 90 = =2·5·3·3 | 0,695 | 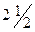
| 0,0314 | ||||||
| 90 = =2·5·3·3 | 0,59 | 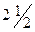
| 0,0314 | ||||||
| 90 = =2·5·3·3 | 0,402 | 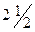
| 0,0314 |
Пазы и обмотка статора
21. Ширина паза (предварительно) по (10.21)
 м (12 мм).
м (12 мм).
22. Поперечное сечение эффективного проводника обмотки статора (предварительно) по (10.22)
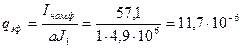 м2 (11,7 мм2),
м2 (11,7 мм2),
где
 А/м
А/м
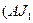 — по рис. 10.16, кривая 2
— по рис. 10.16, кривая 2 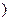 .
.
23. Возможная ширина изолированного проводника по (10.25)
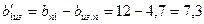 мм.
мм.
Изоляция катушек выбрана для класса нагревостойкости B по табл. 3.5. Двусторонняя толщина изоляции 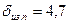 мм.
мм.
24. Размеры проводников обмотки. Принимаем, что эффективный проводник состоит из одного элементарного 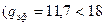 мм2
мм2 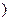 . Марка провода ПЭТВСД с толщиной двусторонней изоляции 0,5 мм. Ширина голого прямоугольного проводника (предварительная) 7,3…0,5 = 6,8 мм.
. Марка провода ПЭТВСД с толщиной двусторонней изоляции 0,5 мм. Ширина голого прямоугольного проводника (предварительная) 7,3…0,5 = 6,8 мм.
По табл. П3.3 размеры медного проводника равны 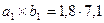 мм (с изоляцией
мм (с изоляцией 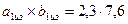 мм),
мм), 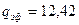 мм (12,42·10-6 мм2).
мм (12,42·10-6 мм2).
25. Ширина паза (уточненная) по (10.27)
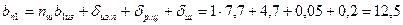 мм.
мм.
26. Высота паза по (10.28)
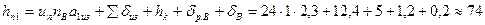 мм,
мм,
где
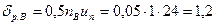 мм.
мм.
Масштабный эскиз паза дан на рис. 10.44, спецификация паза приведена в табл. 0.16.
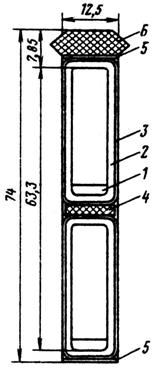
Рис. 10.44. Паз статора
Таблица 10.16. Спецификация паза (изоляция класса нагревостойкости B)
| Позиция на рис. 10.44 | Наименование | Число слоев | Толщина, мм | ||
| по ширине | по высоте | по ширине | по высоте | ||
Провод ПЭТВСД 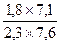 мм мм
| 1 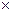 7,6 7,6
| 2(12 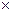 2,3) 2,3)
| |||
| Лента стеклослюдинитовая ЛС 0,13 мм | 6 слоев | Вполнахлеста | 4,5 | 4,5 | |
| Лента стеклянная ЛЭС (покровная) 0,1 мм | 1 слой | Встык | 0,2 | 0,2 | |
| Двусторонняя толщина изоляции одной катушки | — | — | 4,7 | 4,7 | |
| Стеклотекстолит СТ1 толщиной 1 мм | — | — | |||
| Стеклотекстолит СТ1 толщиной 0,5 мм | — | — | |||
| Общая толщина изоляции на паз | — | — | 4,7 | 12,4 | |
| Разбухание изоляции | — | — | 0,05 | 1,2 | |
| Допуск на укладку | — | — | 0,2 | 0,2 | |
| Клин | — | — | — | ||
| Всего | — | — | 12,5 |
27. Уточненное значение плотности тока в проводнике обмотки статора
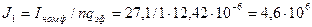 А/м2.
А/м2.
28. Проверка индукции в зубце статора (приближенно) по (10.31):
 Тл.
Тл.
29. Проверка индукции в ярме статора (приближенно) по (10.32):
 Тл;
Тл;
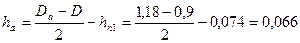 м;
м;
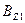 и
и 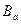 находят в допустимых пределах.
находят в допустимых пределах.
30. Перепад температуры в изоляции паза по (10.33);
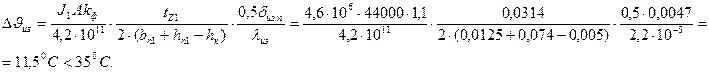
31. Градиент температуры в изоляции паза
 0 С/м.
0 С/м.
Проведенная проверка показала, что размеры паза выбраны удачно.
32. Витки фазы обмотки статора по (10.37)
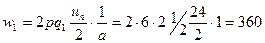 .
.
33. Шаг обмотки по (10.38)
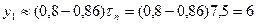 (из 1-го в 7-й паз);
(из 1-го в 7-й паз);
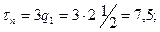
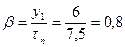 .
.
34. Коэффициент укорочения шага по (10.39)
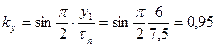 .
.
35. Коэффициент распределения обмотки статора по (10.40)
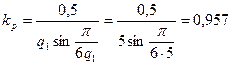 .
.
Так как 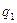 дробное, то в формулу вместо
дробное, то в формулу вместо 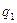 подставляется
подставляется 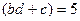 .
.
36. Обмоточный коэффициент по (10.41)
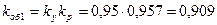 .
.
Воздушный зазор и полюсы ротора
37. Исходя из данных отношения 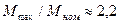 , по рис. 10.18. находим
, по рис. 10.18. находим 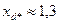 .
.
Приближенное значение воздушного зазора по (10.44)
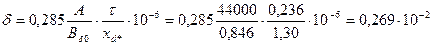 м;
м;
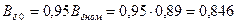 Тл.
Тл.
38. Принимаем воздушный зазор под серединой полюса равным 0,0027 м (2,7 мм). Зазор под краями полюса 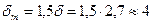 мм. Среднее значение воздушного зазора
мм. Среднее значение воздушного зазора
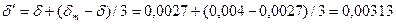 м (3,13 мм).
м (3,13 мм).
39. Ширина полюсного наконечника определяется по (10.47). Примем 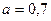 (см. § 10.9):
(см. § 10.9):
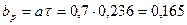 м.
м.
40. Радиус дуги полюсного наконечника по (10.45)
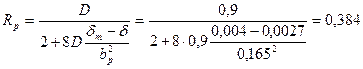 м.
м.
41. Высота полюсного наконечника по табл. 10.9 при 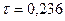 м
м
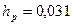 м.
м.
42. Длина сердечника полюса и полюсного наконечника
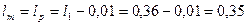 м.
м.
43. Расчетная длина сердечника полюса определяется по (10.52). Принимаем 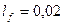 м:
м:
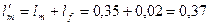 м.
м.
44. Предварительная высота полюсного сердечника по (10.48)
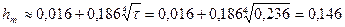 м.
м.
45. Коэффициент рассеяния полюсов находится по (10.50). При 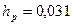 м,
м, 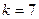 (см. с. 41):
(см. с. 41):
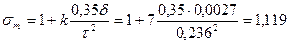 .
.
46. Ширина полюсного сердечника определяется по (10.51). Задаемся 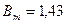 Тл;
Тл; 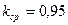 (полюсы выполнены из стали марки Ст3 толщиной 1 мм):
(полюсы выполнены из стали марки Ст3 толщиной 1 мм):
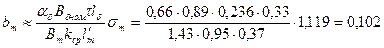 м.
м.
Выбираем 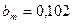 м.
м.
Эскиз полюсов дан на рис. 10.45. Так как
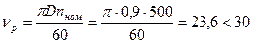 м/с,
м/с,
то принимаем крепление полюсов шпильками к ободу магнитного колеса.
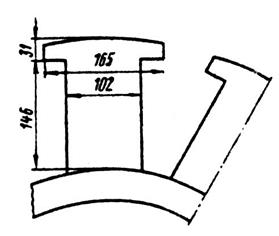
Рис. 10.45. Полюсы ротора
47. Длина ярма (обода) ротора по (10.53)
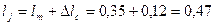 м.
м.
Выбрано 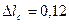 м.
м.
48. Минимальная высота ярма ротора по (10.54)
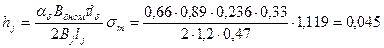 м.
м.
Принято 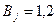 Тл;
Тл; 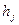 уточняется по чертежу.
уточняется по чертежу.
Пусковая обмотка
49. Число стержней пусковой обмотки на полюс
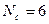
50. Поперечное сечение стержня пусковой обмотки по (10.55)
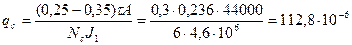 м2.
м2.
51. Диаметр стержня находим по (10.56), материал стержня — медь: 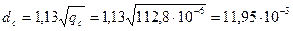 м (11,95 мм).
м (11,95 мм).
Вбираем 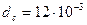 м, тогда
м, тогда 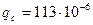 м.
м.
52. Зубцовый шаг на роторе определяется по (10.57). Принимаем 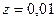 м:
м:
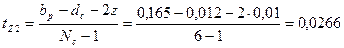 м (26,6 мм)
м (26,6 мм)
53. Проверяем условие (10.60)
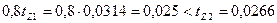 м;
м;
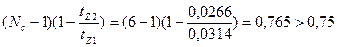 .
.
Пазы выбраны круглые. Полузакрытые.
54. Диаметр паза ротора
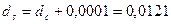 м (12,1 мм).
м (12,1 мм).
Раскрытие паза 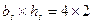 мм.
мм.
55. Длина стержня по (10.61)
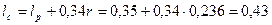 м.
м.
56. Сечение короткозамыкающего сегмента
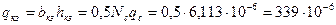 м2 (339 мм2).
м2 (339 мм2).
По табл. П3.6 выбираем прямоугольную медь 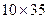 мм (сечение
мм (сечение 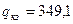 мм2).
мм2).
Расчет магнитной цепи
Для магнитопровода статора выбираем сталь марки 1511 толщиной 0,5 мм. Полюсы ротора выполняют из стали марки Ст3 толщиной 1 мм. Крепление полюсов к ободу магнитного колеса осуществляют с помощью шпилек и гаек. Толщину обода (ярма ротора) принимают 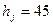 мм (см. выше) (см. приложение 1).
мм (см. выше) (см. приложение 1).
57. Магнитный поток в зазоре по (10.62)
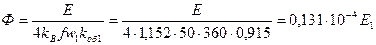 .
.
По рис. 10.21 при 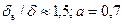 и
и 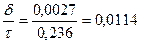 находим
находим 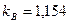 и
и 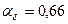 .
.
58. Уточненное значение расчетной длины статора по (10.64) равно:
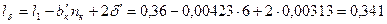 м;
м;
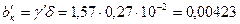 м;
м;
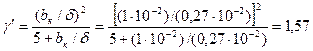 .
.
59. Индукция в воздушном зазоре по (10.63), Тл,
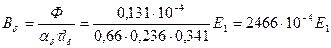 .
.
60. Коэффициент воздушного зазора статора по (10.67)
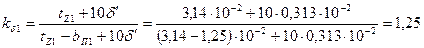 .
.
61. Коэффициент воздушного зазора ротора по (10.67)
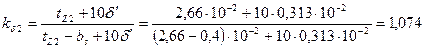 .
.
62. Коэффициент воздушного зазора по (10.66)
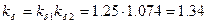 .
.
63. Магнитное напряжение воздушного зазора по (10.65), А,
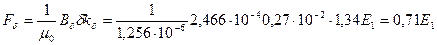 .
.
64. Ширина зубца статора на высоте 1/3 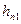 от его коронки по (10.70)
от его коронки по (10.70)
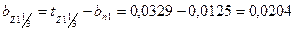 м;
м;
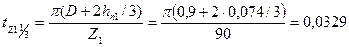 м.
м.
65. Индукция в сечении зубца на высоте 1/3 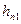 по (10.69), Тл,
по (10.69), Тл,
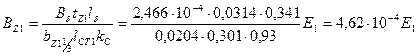 .
.
66. Магнитное напряжение зубцов статора по (10.68), А,
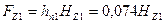 .
.
67. Индукция в спинке статора по (10.74), Тл,
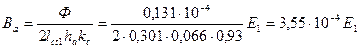 .
.
68. Магнитное напряжение спинки статора по (10.72), А,
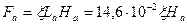 ;
;
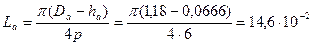 м;
м;
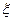 — по рис. 10.22.
— по рис. 10.22.
69. Высота зубцов ротора по (10.76)
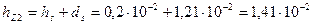 м.
м.
70. Ширина зубцов ротора по высоте 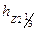 от его коронки по (10.78)
от его коронки по (10.78)

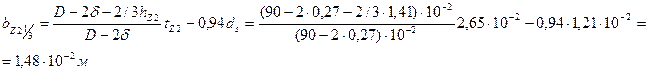
71. Индукция в зубце ротора по (10.77), Тл,
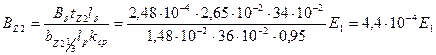 .
.
72. Магнитное напряжение зубцов ротора по (10.75), А,
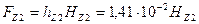 .
.
73. Удельная магнитная проводимость рассеяния между внутренними поверхностями сердечника полюсов по (10.81)
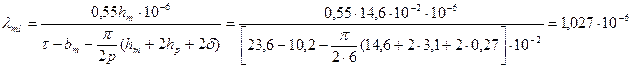 .
.
74. Удельная магнитная проводимость между внутренними поверхностями полюсных наконечников по (10.82)

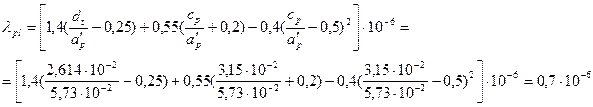
где
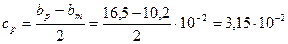 м;
м;
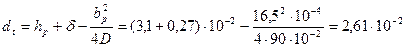 м;
м;
 м.
м.
75. Удельная магнитная проводимость рассеяния между торцевыми поверхностями по (10.83)
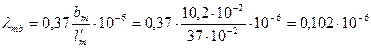 .
.
76. Удельная магнитная проводимость для потока рассеяния
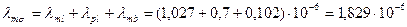 .
.
77. Магнитное напряжение ярма статора, зазора и зубцов полюсного наконечника, А,
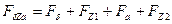 .
.
78. Поток рассеяния полюса по (10.80), Вб,
 .
.
79. Поток в сечении полюса у его основании, Вб,
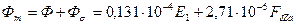 .
.
80. Индукция в полюсе по (10.84), Тл,
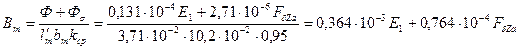 .
.
81. Магнитное напряжение полюса по (10.79), А,
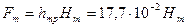 ,
,
где
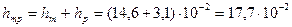 м.
м.
82. Магнитное напряжение стыка между полюсом и ярмом ротора по (10.86), А,
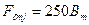 .
.
83. Индукция в ободе магнитного колеса (ярме ротора), по (10.88), Тл,
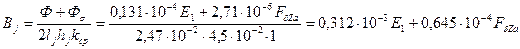 .
.
84. Магнитное напряжение в ободе магнитного колеса по (10.87), А,
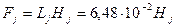 ,
,
где
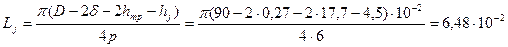 м.
м.
85. Сумма магнитных напряжений сердечника полюса, ярма ротора и стыка между полюсом и ярмом, А,
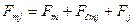 .
.
86. Сумма магнитных напряжений всех участков магнитной цепи, А, (10.89)
 .
.
Результаты расчета магнитной цепи сведены в табл. 10.17.
При переводе магнитных напряжений 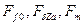 и потоков
и потоков 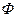 и
и 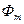 в относительные единицы за базовые значения соответственно приняты МДС
в относительные единицы за базовые значения соответственно приняты МДС 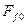 и
и 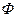 при
при 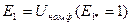 .
.
По табл. 10.17 на рис. 10.46 построена в относительных единицах характеристика холостого хода 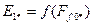 . На этом же рисунке приведена нормальная характеристика холостого хода.
. На этом же рисунке приведена нормальная характеристика холостого хода.
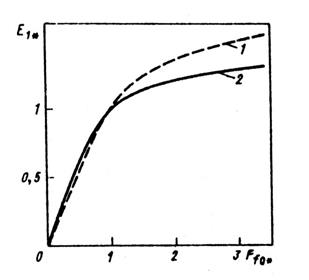
Рис. 10.46. Характеристика холостого хода:
1 — расчетная характеристика;
2 — нормальная характеристика
Таблица 10.17. Результаты расчета магнитной цепи
| Расчетная величина | Единица величины | 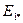 и и 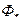
| ||||
| 0,5 | 1,1 | 1,2 | 1,3 | |||
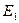
| В | 3814,8 | 4161,6 | 4508,4 | ||
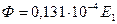
| Вб | 0,0227 | 0,0454 | 0,05 | 0,0545 | 0,0591 |
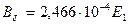
| Тл | 0,428 | 0,86 | 0,941 | 1,026 | 1,112 |
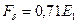
| А | 2462,3 | 2708,5 | 2954,7 | ||
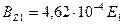
| Тл | 0,8 | 1,6 | 1,76 | 1,92 | 2,08 |
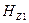
| А/м | |||||
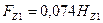
| А | 18,8 | 495,8 | |||
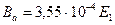
| Тл | 0,62 | 1,23 | 1,35 | 1,48 | 1,6 |
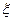
| 0,63 | 0,42 | 0,4 | 0,32 | 0,3 | |
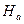
| А/м | |||||
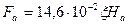
| А | 14,3 | 49,6 | 82,3 | 293,5 | |
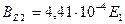
| Тл | 0,76 | 1,53 | 1,68 | 1,84 | 1,99 |
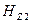
| А/м | |||||
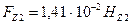
| А | 5,36 | 38,21 | 87,8 | 188,9 | 369,4 |
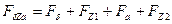
| А | 1269,5 | 3045,9 | 4284,6 | 5446,6 | 8377,9 |
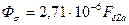
| Вб | 0,0034 | 0,0083 | 0,012 | 0,015 | 0,023 |
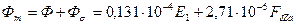
| Вб | 0,026 | 0,0537 | 0,062 | 0,07 | 0,082 |
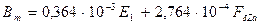
| Тл | 0,73 | 1,49 | 1,72 | 1,93 | 2,28 |
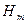
| А/м | |||||
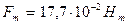
| А/м | 64,25 | 373,5 | |||
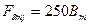
| А | 182,5 | 372,5 | 482,5 | ||
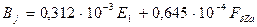
| Тл | 0,622 | 1,276 | 1,47 | 1,63 | 1,95 |
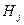
| А/м | |||||
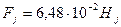
| А | 32,8 | 97,2 | 169,8 | 294,8 | |
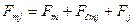
| А | 279,5 | 843,2 | 1440,8 | 2991,3 | |
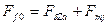
| А | 8437,9 | ||||
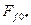
| — | 0,398 | 1,47 | 2,17 | 4,15 | |
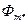
| — | 0,575 | 1,18 | 1,37 | 1,54 | 1,81 |
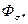
| — | 0,075 | 0,18 | 0,27 | 0,34 | 0,51 |
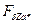
| 0,326 | 0,78 | 1,1 | 1,4 | 2,15 | |
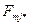
| 0,072 | 0,22 | 0,37 | 0,77 | ||
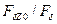
| 1,03 | 1,24 | 1,58 | 1,84 | 2,62 |
Примечания. 1. При определении магнитного напряжения зубцов в тех случаях, когда 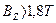 (
(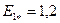 или
или 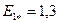 ), учитывалось ответвление потока в паз по коэффициентам:
), учитывалось ответвление потока в паз по коэффициентам:
для статора
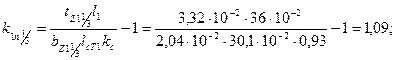
для ротора
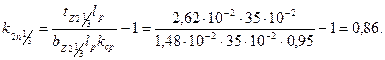
2. При 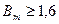 Тл магнитное напряжение полюса определялось по трем сечениям.
Тл магнитное напряжение полюса определялось по трем сечениям.
Параметры обмотки статора для установившегося режима
87. Средняя длина витка обмотки статора
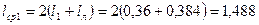 м.
м.
88. Длина лобовой части обмотки статора по (9.139)—(9.143) и рис. 9.49
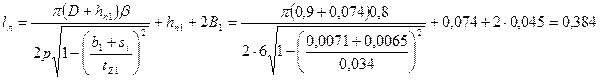 м.
м.
где 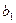 =0,0071 м — ширина проводника;
=0,0071 м — ширина проводника; 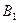 и
и  — по рис. 9.49.
— по рис. 9.49.
89. Активное сопротивление обмотки статора по (10.95)
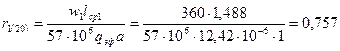 Ом
Ом
при 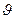 =200 С;
=200 С;
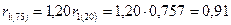 Ом
Ом
при 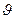 =750 С.
=750 С.
90. Активное сопротивление обмотки статора в относительных единицах по (10.96)
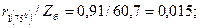
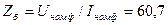 Ом.
Ом.
91. Индуктивное сопротивление рассеяния по (10.97)
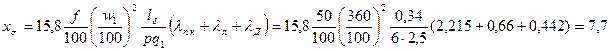 Ом.
Ом.
92. Коэффициент магнитной проводимости пазового рассеяния по (10.98)
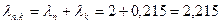 .
.
Коэффициент магнитной проводимости между стенками паза по табл. 9.24
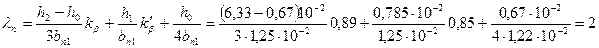
Размеры паза по рис. 8.50, 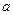 и 10.44:
и 10.44: 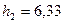 см;
см; 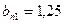 см;
см; 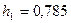 см;
см; 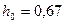 см.
см.
При 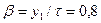 по (9.156) и (9.158)
по (9.156) и (9.158) 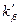 и
и 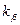 :
:
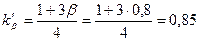 ;
;
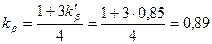 .
.
Коэффициент магнитной проводимости по коронкам зубцов по (10.99)
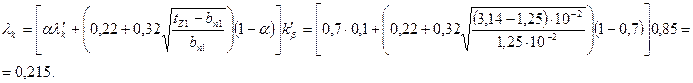
При 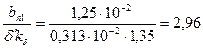 из рис. 10.26
из рис. 10.26 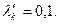
93. Коэффициент магнитной проводимости лобового рассеяния по (9.159)
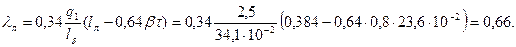
94. Коэффициент магнитной проводимости дифференциального рассеяния по (10.100)
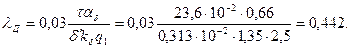
95. Индуктивное сопротивление рассеяния в относительных единицах
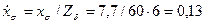 .
.
96. Индуктивное сопротивление продольной реакции якоря в относительных единицах по (10.102)
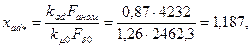
где
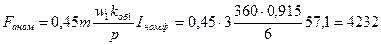 А
А
по (10.90); 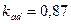 из рис. 10.24. По характеристике холостого хода (см. табл. 10.17) для
из рис. 10.24. По характеристике холостого хода (см. табл. 10.17) для 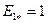 МДС
МДС 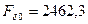 А.
А.
Для ЭДС 
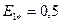

97. Индуктивное сопротивление поперечной реакции якоря в относительных единицах по (10.103)
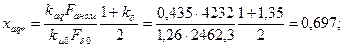
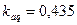 по рис. 10.24
по рис. 10.24
98. Синхронное индуктивное сопротивление по продольной оси в относительных единицах
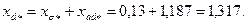
99. Синхронное индуктивное сопротивление по поперечной оси в относительных единицах
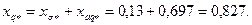
Магнитодвижущая сила обмотки возбуждения при нагрузке
100. По табл. 10.17. на рис. 10.47. построены частичные характеристики намагничивания 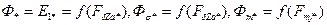 , а на рис. 10.48 — зависимость
, а на рис. 10.48 — зависимость 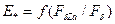 .
.
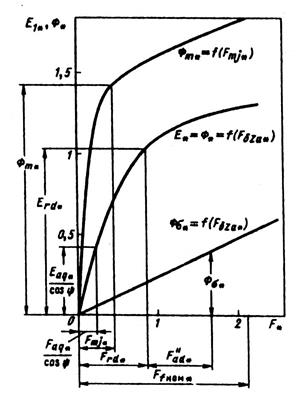
Рис. 10.47. Частичные характеристики намагничивания
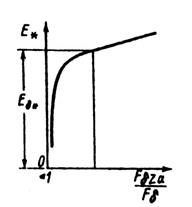
Рис. 10.48. Зависимость 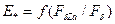
Из векторной диаграммы диаграммы для номинального режима 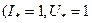 и
и 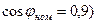 (рис. 10.49) определяем
(рис. 10.49) определяем 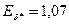 .
.
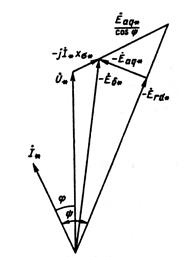
Рис. 10.49. Векторная диаграмма для номинальной нагрузки
Из рис. 10.48 по
Date: 2015-09-05; view: 643; Нарушение авторских прав