
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Префиксный код
Теорема Шеннона о кодировании источников устанавливает связь между средней длинной кодового слова и энтропией источника.
Для любого дискретного источника без памяти X с конечным алфавитом и энтропией H(X) существует D- ичный префиксный код, в котором средняя длинна кодового слова 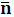 , удовлетворяет неравенству:
, удовлетворяет неравенству:

В префиксном коде никакое кодовое дерево не является префиксом другого кодового дерева. Это значит, что поток кодовых слов может использоваться без специального разделения этих слов. Например, если код 101 является кодом какой-то буквы, то в качестве кодов других букв нельзя использовать следующие комбинации: 1,10,10101, …и т.д.
Из теоремы Шеннона следует, что тем ближе длина кодового слова к энтропии источника, тем более эффективно кодирование. В идеальном случае, когда  , код называют эффективным. Эффективность кода оценивается величиной:
, код называют эффективным. Эффективность кода оценивается величиной:
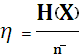 .
.
Если средняя длина 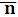 кодового слова является минимально возможной, то код еще и оптимальный. Теорема кодирования источников доказывается с использованием неравенства Крафта и формулируется следующим образом.
кодового слова является минимально возможной, то код еще и оптимальный. Теорема кодирования источников доказывается с использованием неравенства Крафта и формулируется следующим образом.
Для существования однозначно декодируемого D- ичного кода, содержащего k кодовых слов с длинами n1,n2,…,nk, необходимо и достаточно, чтобы выполнялось неравенство Крафта:

1.2 Методы оптимального кодирования. Сжатие данных.
Процедуру оптимального кодирования часто называют сжатием данных. Тогда задача сжатия данных есть минимизация технических затрат на хранение или передачу информации путем оптимального кодирования. На практике используют два вида сжатия данных:
1.Сжатие без потерь - устранение избыточности информации, не связанное с ее изменением, принципиально существенным для пользователя.
2. Сжатие с потерями – устранение избыточности информации, которое приводит к безвозвратной потере некоторой доли информации, хотя это не принципиально для ее восстановления в интересах пользователя.
Сжатие без потерь наиболее применимо к числовым и текстовым данным. Применительно к вычислительной технике сжатие позволяет уменьшить количество бит информации, необходимого для хранения и передачи заданного объема этой информации, что дает возможность передавать сообщения более быстро или хранить более экономно. Такие программные средства, реализующие сжатие, называют архиваторами. Существует достаточно большое их разнообразие.
Методы сжатия данных были разработаны как математическая теория, которая до первой половины 80-х годов 20 века мало использовалась в компьютерной технике.
Методы или алгоритмы сжатия данных без потерь можно разделить на:
1.Статистические методы или алгоритмы. Например, методы Шеннона - Фано, Хаффмана и др.
Они базируются на априорной статистике (вероятностях появления букв алфавита). Это главный недостаток таких кодов, так как априорная статистика кодов заранее не известна, а, следовательно, эффективному кодированию должен предстоять так называемый частотный анализ, т.е. анализ частоты появления символов в кодовой комбинации.
2.Адаптивные методы или алгоритмы. Например, модифицированные коды Хаффмана, арифметическое кодирование и др.
Здесь распределение вероятностей символов сначала считается равномерным на заданном интервале, а потом оно меняется по мере накопления статистики.
3.Динамические методы или алгоритмы. Они являются универсальными и не нуждаются в априорной статистике. Например, метод Лемпела- Зива.
1.2.1 Метод кодирования Шеннона - Фано.
Буквы исходного алфавита записываются в порядке убывания их вероятностей. Это множество разбивается так, чтобы вероятности двух подмножеств были примерно равны. Все буквы верхнего подмножества в качестве первого символа кода получают 1, а буквы нижнего подмножества-0. Затем последнее подмножество снова разбивается на два подмножества с соблюдением того же условия и проводят то же самое присвоение кодовым элементам второго символа. Процесс продолжается до тех пор, пока во всех подмножествах не останется по одной букве кодового алфавита.
Пример.
| Буква xi | Вероятности pi | Кодовая последовательность | Длина кодового слова ni | pini | -pilog2pi | |||
| Номер разбиения | ||||||||
| x1 | 0,25 | 0,5 | 0,5 | |||||
| x2 | 0,25 |  0 0
| 0,5 | 0,5 | ||||
| x3 | 0,15 |  0 0
| 0,45 | 0,4 | ||||
| x4 | 0,15 |  0 0
| 0,45 | 0,4 | ||||
| x5 | 0,05 |  0 0
|  1 1
| 0,2 | 0,2 | |||
| x6 | 0,05 | 0,2 | 0,2 | |||||
| x7 | 0,05 |  0 0
| 0,2 | 0,2 | ||||
| x8 | 0,05 |  0 0
| 0,2 | 0,2 |
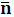 =
=  = (0,25*2+0,25*2+0,15*3+0,15*3+0,05*4+0,05*4+0,05*4+0,15*4)=2,7 бит
= (0,25*2+0,25*2+0,15*3+0,15*3+0,05*4+0,05*4+0,05*4+0,15*4)=2,7 бит
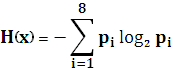 = - (2*0,25*log2 0,25 + 2*0,15*log2 0,15 + 4*0,05*log20,05) = 2,7 бит
= - (2*0,25*log2 0,25 + 2*0,15*log2 0,15 + 4*0,05*log20,05) = 2,7 бит
 =
=  1
1
Метод Шеннона - Фано не всегда приводит к однозначному построению кода, так как при разбиении на подмножества можно сделать большей по вероятности как верхнюю, так и нижнюю часть, следовательно, такое кодирование хотя и является эффективным, но не всегда будет оптимальным.
1.2.2 Метод кодирования Хаффмана.
Этот метод всегда дает оптимальное кодирование в отличие от предыдущего, так как получаемая средняя длина кодового слова является минимальной.
Буквы алфавита сообщения располагают в порядке убывания вероятностей. Две последние буквы объединяют в один составной символ, которому приписывают суммарную вероятность. Далее заново переупорядочивают символы и снова объединяют пару с наименьшими вероятностями. Продолжают эту процедуру до тех пор, пока все значения не будут объединены. Это называется редукцией. Затем строится кодовое дерево из точки, соответствующей вероятности 1 (это корень дерева), причем ребрам с большей вероятностью присваивают 1,а с меньшей-0. Двигаясь по кодовому дереву от корня к оконечному узлу, можно записать кодовое слово для каждой буквы исходного алфавита.
Пример.
| Буква xi | a | b | c | d | e | f |
| Вероятности pi | 0,05 | 0,15 | 0,05 | 0,4 | 0,2 | 0,15 |
| Кодовое слово | ||||||
| Длина кодового слова ni |
|





|


|









|
|





|
|
|
|
|
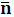 =
=  = (4*0,05 +3*0,15+4*0,05+0,4+3*0,2+3*0,15)= 2,3 бит
= (4*0,05 +3*0,15+4*0,05+0,4+3*0,2+3*0,15)= 2,3 бит
 = - (0,4log2 0,4+0,2 log2 0,2+2* 0,15 log20,15 +2*0,05 log20,05)= - (0,52 + 0,46+ 2*0,4+2*0,2)= 2,18
= - (0,4log2 0,4+0,2 log2 0,2+2* 0,15 log20,15 +2*0,05 log20,05)= - (0,52 + 0,46+ 2*0,4+2*0,2)= 2,18
 =
=  1,05
1,05
Из рассмотренного примера видно, что чем больше разница между вероятностями букв исходного алфавита, тем больше выигрыш кода Хаффмана по сравнению с простым блоковым кодированием.
Декодирование блока Хаффмана легко представить, используя кодовое дерево. Принятая кодовая комбинация анализируется посимвольно, в результате чего, начиная с корня дерева, мы попадаем в оконечный узел, соответствующий принятой букве исходного алфавита.
Недостатки кода:
1.Различные длины кодовых слов приводят к неравномерным задержкам кодирования.
2.Сжатие снижает избыточность, что соответственно повышает предрасположенность к распространению ошибок, т.е. один ошибочно принятый бит может привести к тому, что все последующие символы будут декодироваться неверно.
3.Предполагаются априорные знания вероятности букв, которые на практике не известны, а их оценки часто бывают затруднительны.
4.3.3. Арифметическое кодирование.
Алгоритм Хаффмана не может передавать на каждый символ сообщения, если не использовать блоковое кодирование, менее одного бита информации, хотя энтропия источника может быть меньше 1, особенно при существовании различных вероятностей символов.

Поэтому хотелось бы иметь такой алгоритм кодирования, который позволял бы кодировать символы менее чем 1 бит. Одним из таких алгоритмов является арифметическое кодирование, представленное в 70-х годах 20 века. При рассмотрении этого алгоритма будем исходить из того факта, что сумма вероятностей символов (и соответствующим им относительным частотам появления этих символов), всегда равна 1.Отсительные частоты появления могут определяться путем текущих статистических измерений исходного сообщения (это первый «проход» процедуры кодирования). Особенностью арифметического кодирования является то, что для отображения последовательности символов на интервале [0,1] используются относительные частоты их появления.
Пример определения частоты появления символов в сообщении
BANANANBAB.
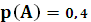
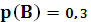
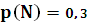
Результатом такого отображения является сжатие символов или посимвольное сжатие в соответствии с их вероятностями, т.е. результатом арифметического сжатия будет некоторая дробь из интервала [0,1], который представляется двоичной записью (это второй «проход» процедуры кодирования). Заметим, что такой двухпроходный алгоритм может быть реализован в ранее рассмотренных кодах Шеннона – Фано и Хаффмана.
Принципиальное отличие арифметического кодирования от предыдущих методов заключается в том, что кодированию подвергается сообщения целиком (весь набор символов или файл), а не символы по отдельности или их блоки.
Эффективность арифметического кодирования растет с увеличением длины сжимаемого сообщения. Заметим, что в кодах Шеннона – Фано и Хаффмана такого не происходит.
Арифметическое кодирование заключается в построении отрезка, однозначно определяющего заданную последовательность символов в соответствии с их вероятностями. Объединение всех отрезков, пересекающихся только в граничных точках, для вероятностей каждого символа должно образовывать формальный интервал [0,1]. Для последнего полученного интервала, соответствующего последнему принятому символу сообщения, находит число, принадлежащее его внутренней части. Это число в двоичном представлении и будет кодом для рассматриваемой последовательности.
Пример. Пусть задан алфавит X={a,b}, p(a) = 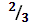 , p(b) =
, p(b) = 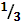 . Необходимо закодировать сообщение {aba}.
. Необходимо закодировать сообщение {aba}.
| Шаг кодирования | Поступающий символ | Интервал |
| нет | [ 0,1 ] | |
| a | [ 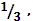 1] 1]
| |
| b | [  ] ]
| |
| a | 
|
|
|





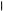
 1.
1.
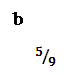 |
| ||||||
| |||||||





 2.
2.
 | ||||||
|
|
1.  ,
,
2.  ,
,
3. 

|
|
|



 3.
3.
 | ||||||
|
| |||||
1.  ,
,
2.  ,
,
3. 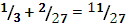
В таком алгоритме в конце сообщения должен стоять некий маркер, обозначающий конец сообщения.

Код сообщения {aba}=10000.
Декодирование арифметического кода производится по его значению и тем же интервалам до восстановления исходного сообщения. На практике часто используют адаптивный арифметический алгоритм, когда на начальном этапе относительные частоты появления символов задаются некоторыми отрезками, либо принимаются равновероятными. А в процессе кодирования значение этих частот уточняются.
| <== предыдущая | | | следующая ==> |
| Глава пятнадцатая | | | Нормальное уравнение плоскости в векторной и координатной формах (вывод) |
Date: 2015-09-05; view: 979; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |


