Определение критериев подобия способом интегральных аналогов

Определим число критериев подобия и число форм их записи:

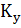= n – 1 + a = 5 – 1 + 1 = 5

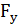= n = 5

Перенесем все члены уравнения в одну сторону:

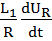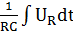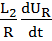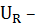
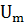+ + + sin ωt = 0 (1.1)

1.1 В первой форме записи

Найдем критерии подобия в первой форме записи. Для этого разделим все члены уравнения (1.1) на первый член, то есть на :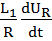

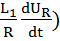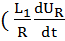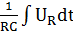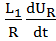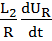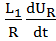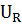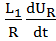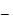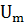(: ) + ():() + ():() + ():() ( sin ωt):(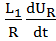) = 0 (1.2)

Далее зачеркиваем, а затем исключаем знаки дифференцирования и интегрирования и неоднородные функции. После вышеописанных преобразований уравнения (1.2) получаем выражение:

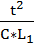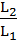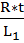
1 + + + 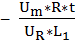= 0

В соответствии с первой теоремой подобия имеем пять критериев подобия. При этом стоит отметить, что четыре из них являются основными и имеют пять форм записи, и один дополнительный критерий подобия, который всегда имеет единственную форму записи.

Запишем критерии подобия в первой форме:

= , = = , = , =

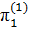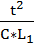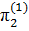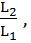
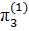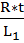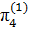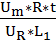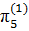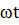
1.2 Во второй форме записи

По аналогии проделаем те же вычисления, которые были приведены в пункте 1.1 для второй и последующих форм записи. Разделим все члены уравнения (1.1) на :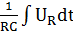

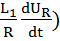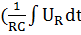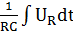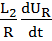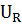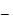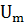(: ) + ():() + ():() + + ():() ( sin ωt):(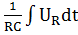) = 0 (1.3)

После математических преобразований выражения (1.3) и исключения из него всех знаков интегрирования и дифференцирования и неоднородных функций, получим:

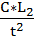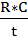
+ 1 + + = 0

Запишем найденные критерии подобия во второй форме:

= , = , = , = , =

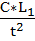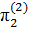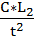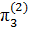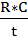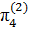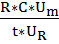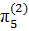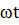
1.3 В третьей форме записи

Проделаем аналогичные преобразования для нахождения третьей формы записи. Разделим все члены уравнения (1.1) на :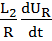

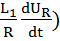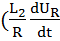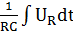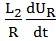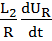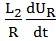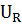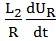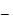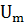(: ) + ():() + ():() + ():() ( sin ωt):(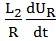) = 0 (1.4)

Преобразуя выражение (1.4) путем исключения из него всех знаков интегрирования и дифференцирования и неоднородных функций, получаем:

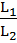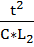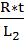
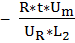+ + 1 + = 0

Запишем найденные критерии подобия в третьей форме:

, , = , = , =

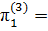
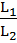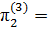
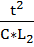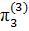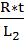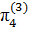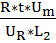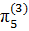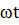
1.4 В четвертой форме записи

Проведем аналогичные преобразования для нахождения четвертой формы записи. Для этого разделим все члены уравнения (1.1) на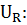

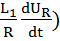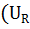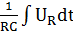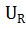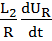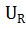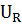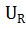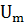(: ) + ():() + ():() + ():() – – ( sin ωt):(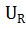) = 0 (1.5)

Упростив выражение (1.5) и исключив из него все знаки интегрирования и дифференцирования и неоднородные функции, получаем:

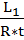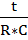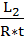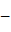
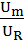+ + + 1 = 0

Запишем найденные критерии подобия в четвертой форме записи:

= , = , = , = , =

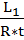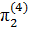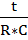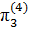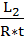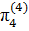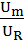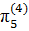1.5 В пятой форме записи

Проделаем аналогичные преобразования для нахождения пятой формы записи критериев подобия. Для этого разделим все члены уравнения (1.1) на :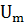

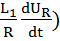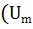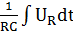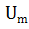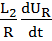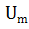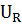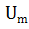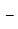
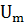(: ) + ():() + ():() + ():() ( sin ωt):(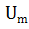) = 0 (1.6)

После математических преобразований и исключения из выражения (1.6) знаков дифференцирования и интегрирования и неоднородных функций, получим следующее выражение:

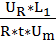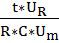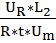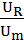
+ + + 1 = 0

Запишем найденные критерии подобия в пятой форме записи:

= , = , = , = , =

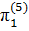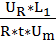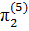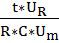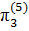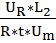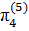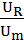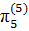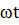
Date: 2015-09-05; view: 742; Нарушение авторских прав