
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Входящий поток требований
|
|
Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени. Поток событий называется регулярным, если события следуют одно за другим через одинаковые, строго фиксированные промежутки времени. Для многих реальных процессов поток требований достаточно хорошо описывается законом распределения Пуассона, согласно которому вероятность 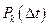 того, что в обслуживающую систему за промежуток время Δ t поступит именно k требований, равна
того, что в обслуживающую систему за промежуток время Δ t поступит именно k требований, равна
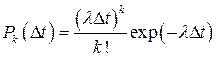 .
.
Где λ — среднее число требований, поступивших на обслуживание в единицу времени.
Такой поток является простейшим.
Простейший поток обладает такими важными свойствами:
1. Свойство стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погрузку, в среднем в сутки должно быть одинаковым для различных периодов времени, к примеру, в начале и в конце декады.
2. Отсутствие последействия, которое обуславливает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени. Например, число автомобилей, прибывших за материалами в десятый день месяца, не зависит от числа автомобилей, обслуженных в четвертый или любой другой предыдущий день данного месяца.
3. Свойство ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).
На практике условия простейшего потока не всегда строго выполняются. Часто имеет место нестационарность процесса (в различные часы дня и различные дни месяца поток требований может меняться, он может быть интенсивнее утром или в последние дни месяца). Существует также наличие последействия, когда количество требований на отпуск товаров в конце месяца зависит от их удовлетворения в начале месяца. Наблюдается и явление неоднородности, когда несколько клиентов одновременно пребывают на склад за материалами. Однако в целом пуассоновский закон распределения с достаточно высоким приближением отражает многие процессы массового обслуживания. Почему такое предположение в ряде важных случаев оказывается верным, дает ответ теорема А.Я.Хинчина. Эта теорема имеет место в случае, когда входящий поток можно представить в виде суммы большого числа независимых потоков, ни один из которых не является сравнимым по интенсивности со всем суммарным потоком. Приведем “не строгую” формулировку этой теоремы.
Теорема (А.Я.Хинчин) Если входящий поток представляет собой сумму большого числа независимых между собой стационарных и ординарных потоков, каждый из которых вносит малый вклад в общую сумму, то при одном дополнительном условии аналитического характера (которое обычно выполняется на практике) поток близок к простейшему.
Применение этой теоремы на практике можно продемонстрировать, на следующем примере: поток судов дальнего плавания в данный грузовой порт, связанный со многими портами мира, можно считать близким к простейшему. Это дает нам право считать поток прибытия судов в порт распределенным согласно процесса Пуассона.
Кроме того, наличие пуассоновского потока требований можно определить статистической обработкой данных о поступлении требований на обслуживание. Известно, что для него распределение промежутков времени между соседними событиями подчиняется экспоненциальному закону: 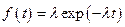 , для которого математическое ожидание и корень из дисперсии равны
, для которого математическое ожидание и корень из дисперсии равны
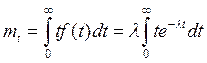 ,
, 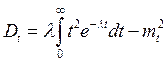 .
.
Интегрируя по частям, получим:
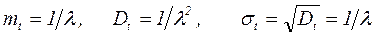 . (7.1)
. (7.1)
Потоки Пальма или потоки с ограниченным последействием являются обобщением потоков элементарных событий. Потоком Пальма называется поток, в котором промежутки времени между двумя соседними событиями представляют собой независимые случайные величины, распределенные по одному и тому же закону. Частным случаем потоков Пальма являются простейшие потоки, в которых интервалы между соседними событиями распределены по показательному закону. Если интервалы между событиями подчиняются гауссовскому распределению, то такие потоки называются нормальными. Очевидно, что для регулярного потока закон распределения выражается d -функцией.
В теории массового обслуживания широко используются потоки Эрланга. Они образуются из простейших потоков путем применения к ним операции "просеивания". Эта операция заключается в том, что из простейшего потока удаляется некоторое число точек по определенному правилу. Если удаляются точки через одну, т.е. остается каждая 2-я точка, то поток Эрланга называется потоком 2-го порядка (Э2). Если удаляются две точки подряд и остается каждая 3-я точка, то получается поток Эрланга 3-го порядка (Э3). Если удаляются (k -l) точек подряд, а остается каждая k -я точка, то поток Эрланга называется потоком k -го порядка (Э k). Очевидно, что простейший поток является потоком Эрланга 1-го порядка.
Можно показать, что функция распределение промежутков времени между соседними событиями имеет вид
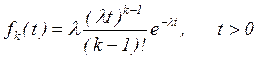 .
.
Это так называемый закон Эрланга. При k =1 он вырождается в показательное распределение.
Каждый интервал в потоке Э k равен: Т = STi, где Ti - независимые случайные величины, распределенные по показательному закону с первыми двумя моментами, определяемыми выражениями (7.1). Применяя теоремы о сложении математических ожиданий и дисперсий для суммы независимых случайных величин, получим
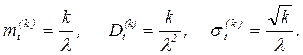
Date: 2015-09-05; view: 837; Нарушение авторских прав