Матричные уравнения

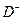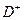Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Представим сеть Петри в виде двух матриц и , представляющих входную и выходную функции. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим

(5.2)

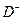определяет входы в переходы, 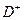— выходы.

Пусть e [ j ] — m -вектор, содержащий нули везде, за исключением j -й компоненты. Переход t_j представляется m -вектором e [ j ] (строка), а маркировка m — n -вектором (столбец). Теперь переход t_j в маркировке m разрешен, если m 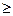e [ j ] • 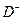, а результат запуска перехода t_j в маркировке m записывается как

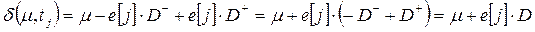. (5.3)

где D = 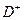- 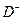— составная матрица изменений.

Для последовательности запусков переходов 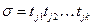имеем

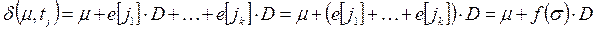. (5.4)

Вектор 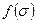называется вектором запусков последовательности 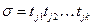. l -ый элемент вектора 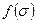— это число запусков перехода 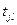в последовательности .

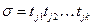Сохранение.

Для того чтобы показать сохранение, необходимо найти (ненулевой) вектор взвешивания, для которого взвешенная сумма по всем достижимым маркировкам постоянна. Пусть w — n - вектор-столбец. Тогда, если m — начальная маркировка, а m ' — произвольная достижимая маркировка, необходимо, чтобы m • w = m ' • w. Теперь, поскольку m ' достижима, существует последовательность запусков переходов 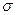, которая переводит сеть из m в m '. Поэтому

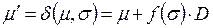. (5.5)

Следовательно, m • w = m ' • w = (m + 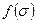• D) • w = m • w + 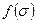• D • w, поэтому 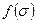• D • w = 0. Поскольку это должно быть верно для всех 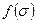, имеем D • w = 0. Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой положительный вектор w, что D • w = 0. Это обеспечивает простой алгоритм проверки сохранения, а также позволяет получать вектор взвешивания w.

Достижимость.

Предположим, что маркировка m ' достижима из маркировки m. Тогда существует последовательность (возможно, пустая) запусков переходов 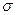, которая приводит из m к m '. Это означает, что 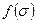является неотрицательным целым решением матричного уравнения:

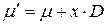. (5.6)

Пример.

Рассмотрим маркированную сеть Петри на рис. 5.1. Матрицы 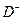, 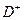и D имеют вид:

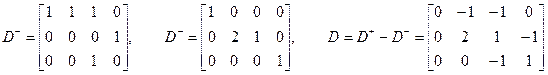. (5.7)

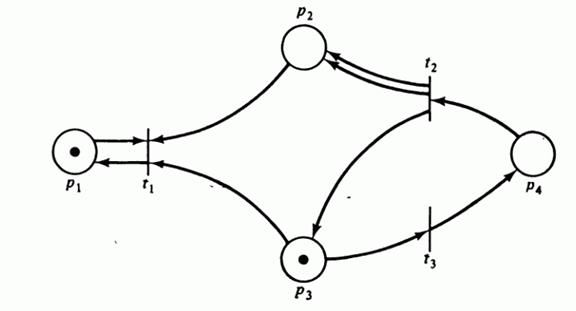
Рис 5.1: Пример сети Петри (решение задачи достижимости).

Для определения того, является ли маркировка (1, 8, 0, 1) достижимой из маркировки (1, 0, 1, 0), имеем уравнение

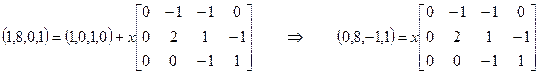. (5.8)

которое имеет решение х = (0, 4, 5). Это соответствует, например, последовательности 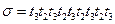. (В принципе, может быть и другая последовательность.)

Матричный подход к анализу сетей Петри очень перспективен, но имеет и некоторые трудности. Заметим прежде всего, что матрица D сама по себе не полностью отражает структуру сети Петри. Переходы, имеющие как входы, так и выходы из одной позиции (петли), представляются соответствующими элементами матриц 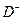и 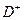, но затем взаимно уничтожаются в матрице D.

Другая проблема — это отсутствие информации о последовательности запусков.

Еще одна трудность заключается в том, что наличие целочисленного решения уравнения (5.6) является необходимым для достижимости, но недостаточным. Рассмотрим простую сеть Петри, приведенную на рис. 5.2. Если мы хотим определить, является ли маркировка (0, 0, 0, 1) достижимой из маркировки (1, 0, 0, 0), необходимо решить уравнение

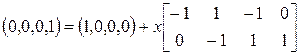. (5.9)

Это уравнение имеет решение (1, 1), соответствующее двум последовательностям: 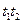и 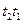. Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни ни 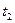не разрешены.

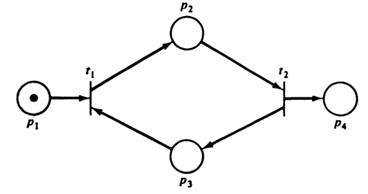
Рис 5.2: Сеть Петри, показывающая, что решение матричного уравнения —

Date: 2015-09-05; view: 1243; Нарушение авторских прав