Упражнение 3.2

1. Определите точки равновесия следующих скалярных дифференциальных уравнений и определите их стабильность:

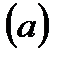
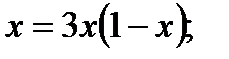
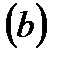
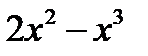
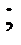
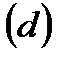
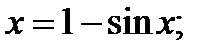
3.3 Бифуркации

Теория бифуркаций изучает возможные изменения в структуре орбиты дифференциального уравнения в зависимости от параметров. Существует два различных аспекта теории бифуркаций: статический и динамический. Статическая теория бифуркаций связана с изменениями, которые происходят в структуре множества нулей функции, в то время как параметры функции разнообразны. В дифференциальных уравнениях равновесными решениями являются нули векторного поля. Таким образом, методы в теории статической бифуркации имеют прямое действие.

Теория динамической бифуркации связана с изменениями, которые происходят в структуре решения дифференциальных уравнений, в то время как параметры векторного поля различны. Изменение качественных свойств может означать изменение в устойчивости исходной системы, таким образом, система должна брать на себя состояние, отличное от начального образца. В таких расплывчатых понятиях, значения параметров в местах, где эти изменения имеют место, называются бифуркационными значениями. Знание бифуркационных значений необходимо для полного понимания системы. Рассмотрим следующее дифференциальное уравнение

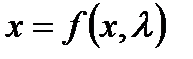, (3.3.1)

где 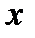определяется в некотором пространстве, 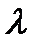представляет собой вектор – параметр, а 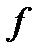- вектор – функцию, который удовлетворяет некоторым требованиям. Там могут существовать различные типы решений, таких как стационарные решения, периодические решения, субгармонические решения, асимптотически квазипериодические решения, хаос, и т.д.

Рассмотрим уравнение равновесия 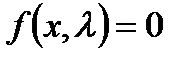. Иногда производные не требуются, и далее в этом параграфе будем считать, что имеет столько производных, сколько необходимо, если это прямо не указано (не очевидно). Мы можем рассматривать равновесные состояния как функции от параметров. Обычно множество равновесий могут существовать при заданных значениях параметров. Основной вопрос для обсуждения путей равновесия зависит от параметров. Рассмотрим некоторые конкретные примеры, иллюстрирующие некоторые из ключевых идей теории бифуркации.

Пример Гиперболическое равновесие нечувствительно.

Рассмотрим линейное дифференциальное уравнение

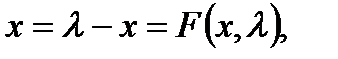(3.3.2)

где 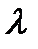- вещественный параметр. При 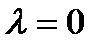, имеем

.

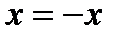Таким образом, из уравнения (3.3.2) имеем нарушение 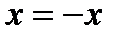. При всех значениях 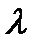существует только одно гиперболическое равновесие, которое является асимптотически стабильным. Перед тем, как сделать вывод из этого примера, мы должны отметить существование неявной функции. Бифуркационная (статическая) задача эквивалентна изучению кривых 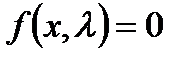и их особых точек. Основным инструментом для доказательства существования является теорема о неявной функции, которая имеет место для вектор - функций нескольких параметров. Для одномерной задачи, теорема формулируется следующим образом.

Лемма 3.3.1 (Теорема о неявной функции в 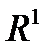) Пусть 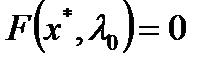и 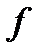есть в 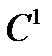в некоторой открытой окрестности 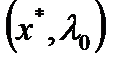. Тогда если 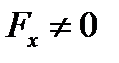на 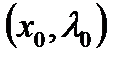, то существуют 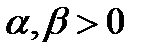такие, что (1) уравнение 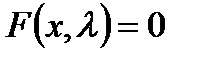имеет единственное решение 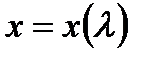при 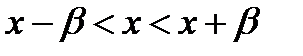всякий раз, когда 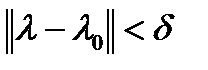; и (2) 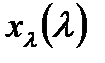существует и

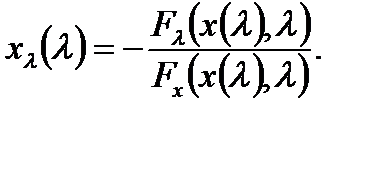
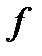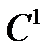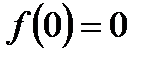Мы знаем, что если - функция класса и при и 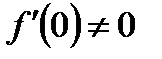, то свойства устойчивости точки равновесия 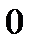из 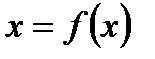определяются линейной аппроксимацией векторного поля вблизи 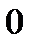, то есть более высокий порядок возмущений в разложении Тейлора векторного поля не влияет на качественный состав потока вблизи нуля. Но мы не рассматривали, что произойдет с системой, если мы сделаем возмущения меньше. Чтобы точно ответить на этот вопрос, рассмотрим возмущенное дифференциальное уравнение

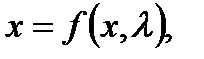
где

-

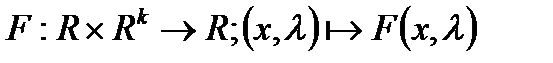есть функция класса 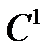, удовлетворяющая

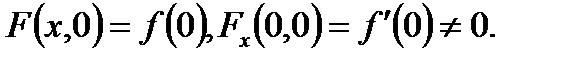
Так как 0 является гиперболической точкой равновесия дифференциального уравнения 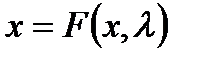, зависящего от 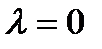, то условия теоремы о неявной функции выполняются. Это гарантирует, что уравнение 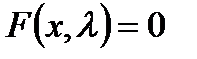должно быть решено локально, в зависимости от параметров

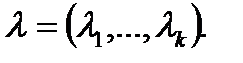
Кроме того, 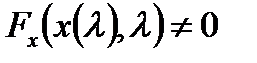для 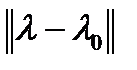достаточно мало. Тип устойчивости равновесия 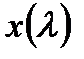такой же, как и тип равновесия 0 (нуля) невозмущенного уравнения 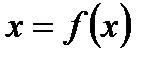. Таким образом, качественный состав потока не меняется вблизи равновесия. Следовательно, в окрестности равновесия нет бифуркаций. Таким образом, мы делаем вывод, что в движение вблизи точки гиперболического равновесия нечувствительно к малым возмущениям векторного поля.

Пример Седлоузловая бифуркация.

Квадратичное дифференциальное уравнение

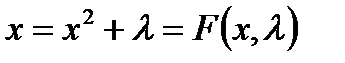, (3.3.3)

где 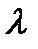- вещественный параметр и он является возмущением 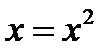. Обратите внимание, что происхождение негиперболической точки равновесия для 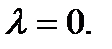Мы можем легко определить движение уравнения (3.3.3) для всех значение параметра 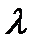, оставляя исходную (оригинальную) параболу 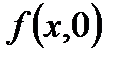фиксированной и вертикально переводящую ось Х по 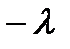. Результаты потоков показаны на рисунке 3.3.1. Для всех 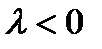система имеет две точки равновесия. Для 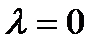система имеет одну и только одну точку равновесия 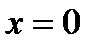. Для всех 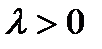у системы нет точек равновесия. Если 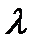изменяется, то до тех пор, пока оно отрицательно, количество и направление орбит остаются теми же; единственное изменение состоит в смещении расположения точек равновесия. Кроме того, для всех положительных 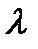есть только одна орбита, и она имеет направление слева направо. Тем не менее, для 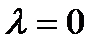, независимо от того как мало изменяется размер 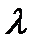, число орбит меняется: существует две точки равновесия для любых 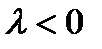и ни одной для .

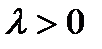Для скалярного дифференциального уравнения 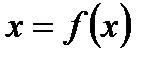, точки равновесия и знак функции 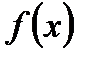между равновесием определяет число орбит и направление потока на орбите. Мы имеем в виду число орбит и направление потока на орбитах в качестве орбитальной структуры дифференциального уравнения или качественной структуры (качественного состава) потока.

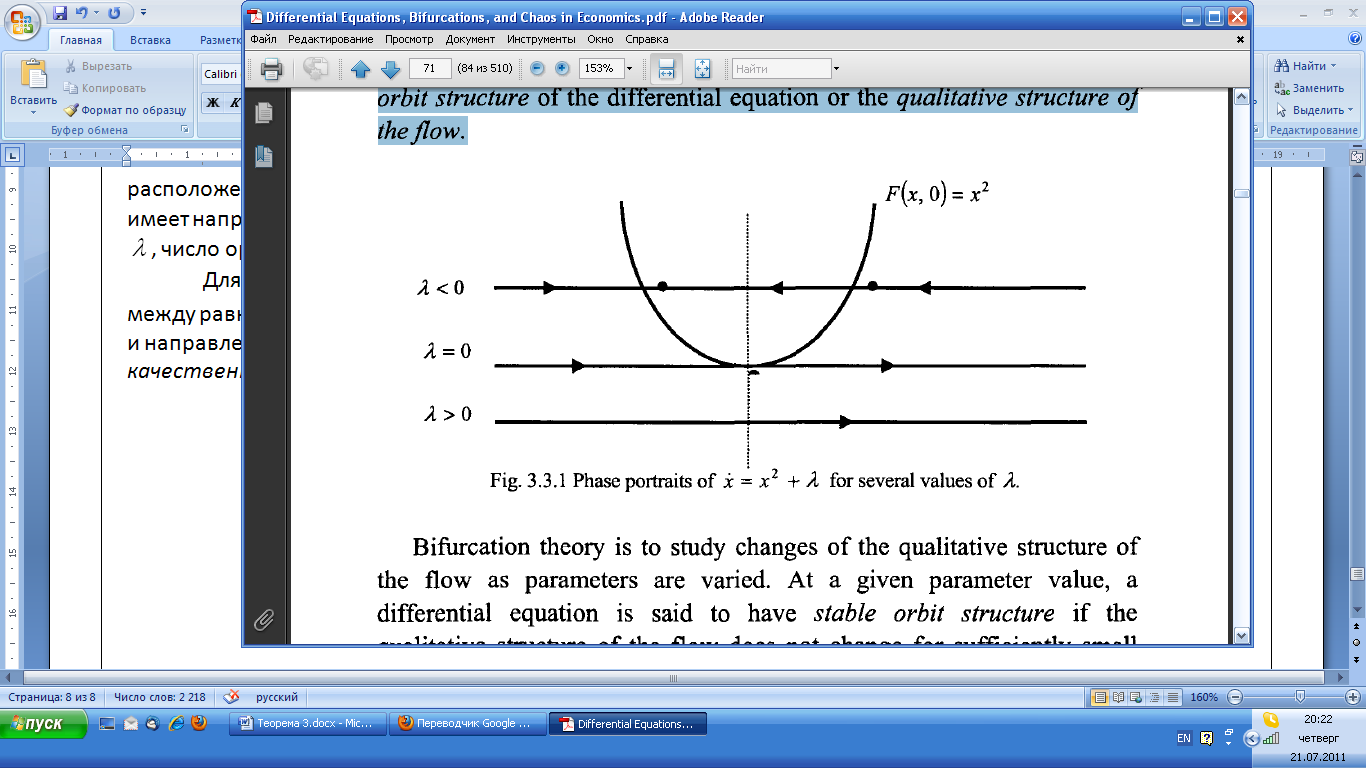
Теория бифуркаций предназначена для изучения изменений качественной структуры потока, согласно различным параметрам. При данном значении параметра дифференциальное уравнение называется устойчивой структурой орбиты, если качественный состав потока не меняется при достаточно малых изменениях параметров. Значение параметра, для которого поток не имеет стабильной структуры орбиты, называют бифуркационным значением, а уравнение называется точкой бифуркации. В приведенном выше примере, уравнение (3.3.3) имеет устойчивую структуру орбиты для любых 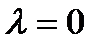. Бифуркация, которой подвергается уравнение (3.3.3), называется седлоузловой бифуркацией. Эта бифуркация имеет также такие названия, как предельная точка и точка возврата.

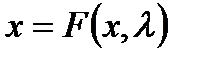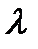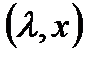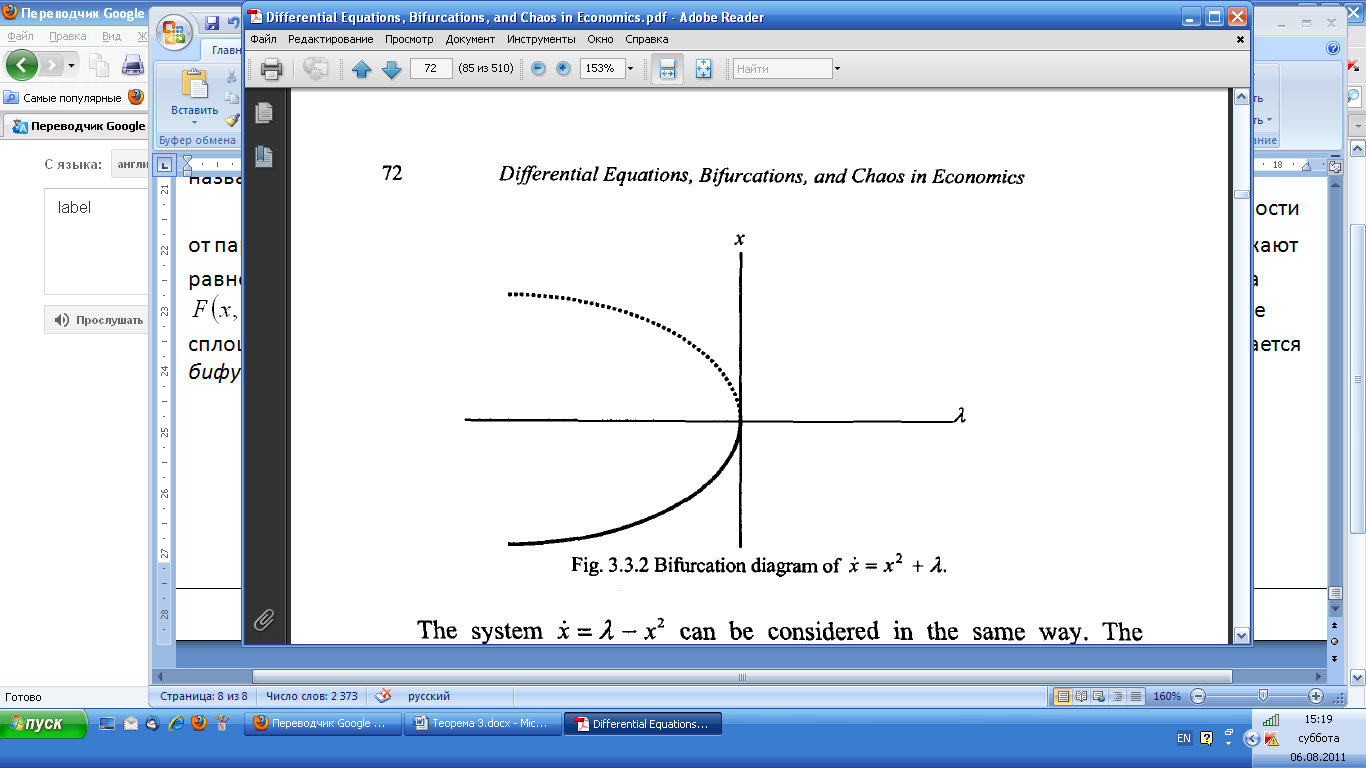
Мы можем изобразить некоторые из важных динамических особенностей , в зависимости от параметра . Графический метод состоит из кривых на чертеже -плоскости, где кривые изображают равновесие для каждого из параметров. Точка лежит на одной из этих кривых тогда и только тогда, когда 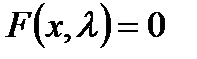. Чтобы представить типы устойчивости этого равновесия, мы отметим устойчивое равновесие сплошными кривыми и неустойчивое равновесие пунктирными кривыми. Конечное изображение называется бифуркационным графиком. Рисунок 3.3.2 – бифуркационный график для

.

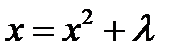Система 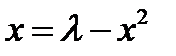может быть рассмотрена тем же самым образом. Анализ показывает два равновесия, появляющихся при 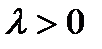. Бифуркационные диаграммы не являются полностью случайными. Различные слои бифуркационных графиков в общих системах проявляют сходства в различных приложениях. Для обсуждения этой темы нам необходимо решить, когда динамические системы имеют качественные аналогичные или эквивалентные бифуркационные графики. Прежде чем продолжить, введем понятие, которое определяет эквивалентность двух динамических систем. Рассмотрим две динамические системы

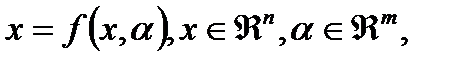(А)

и

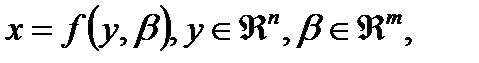(В)

с одинаковыми правыми частями и тем же числом переменных и параметров.

Определение 3.3.1 Динамическая система (А) называется топологически эквивалентной динамической системе (В), если (i) существует гомеоморфизм пространства параметров:

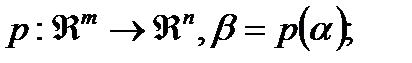
и если (ii) есть параметр – зависимый гомеоморфизм фазового пространства

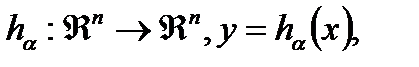
отображение орбит системы (А) при значениях параметра 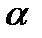на орбитах системы (В) при значениях параметра 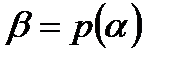, сохраняя направление времени.

По определению, топологически эквивалентные системы, зависящие от параметров, имеют эквивалентные бифуркационные графики. Гомеоморфизм – обратимое отображение, такое, что обе карты (таблицы) вместе с обратными себе непрерывны. В приведенном выше определении мы не требуем непрерывной зависимости гомеоморфизма 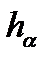от 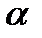. По этой причине приведенное выше определение иногда называют слабой или?(fiber) топологической эквивалентностью.

С точки зрения топологической эквивалентности, следующие теоремы показывают, что система (3.3.3) – вполне «общий» случай, независимо от ее простоты.

Лемма 3.3.2 Система

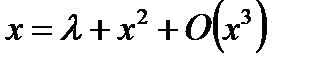
«локально» топологически эквивалентна вблизи начала координат системе

.

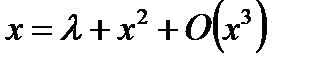Здесь, «локально» означает, что Определение 3.3.1 модифицировано для локального поведения систем.

Теорема 3.3.1 (Топологическая нормальная форма для седлоузловой бифуркации) Любая общая однопараметрическая система

,

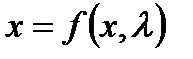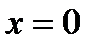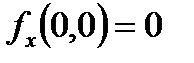имеющая равновесие в точке , при и при 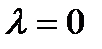, локально топологически эквивалентна вблизи начала координат одной из следующих нормальных форм

.

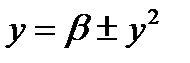Здесь, «общая» значит, что система удовлетворяет ряду условий общности (типичности). Эти условия имеют форму неравенств:

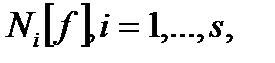
где 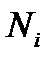- некоторая алгебраическая функция определенных частных производных 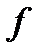, относительно 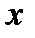и 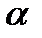, оцененных по .

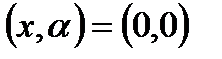Пример Динамика рынка труда.

Рассмотрим простую частично аналитическую модель рынка труда. Положим 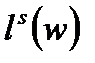и 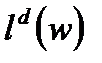- спрос и предложение соответственно, каждое из которых зависит от реальной заработной платы 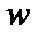. Изменение реальной заработной платы, предполагается, зависит от избыточного спроса на работу силу на этом рынке, то есть

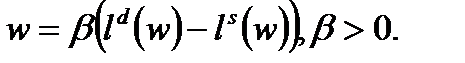
Предположим, что функция спроса параметризована 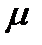и положим

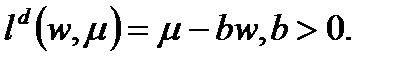
Предположим, что функция предложения труда, отражающая недостатки, такова, что она прогибается назад при больших значения, см. Рис. 3.3.3.

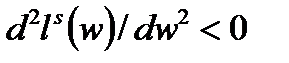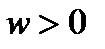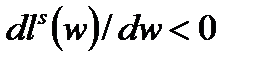Положим для любых и для 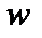, превышающего значение 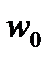. Рассмотрим

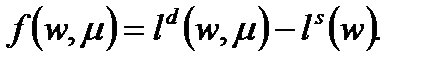
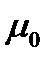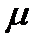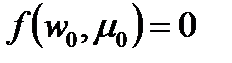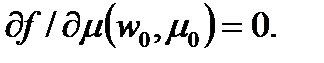Положим - значение такой, что и При 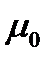функции спроса и предложения касаются друг друга. Таким образом, в этой модели рынка труда седлоузловая бифуркация происходит.

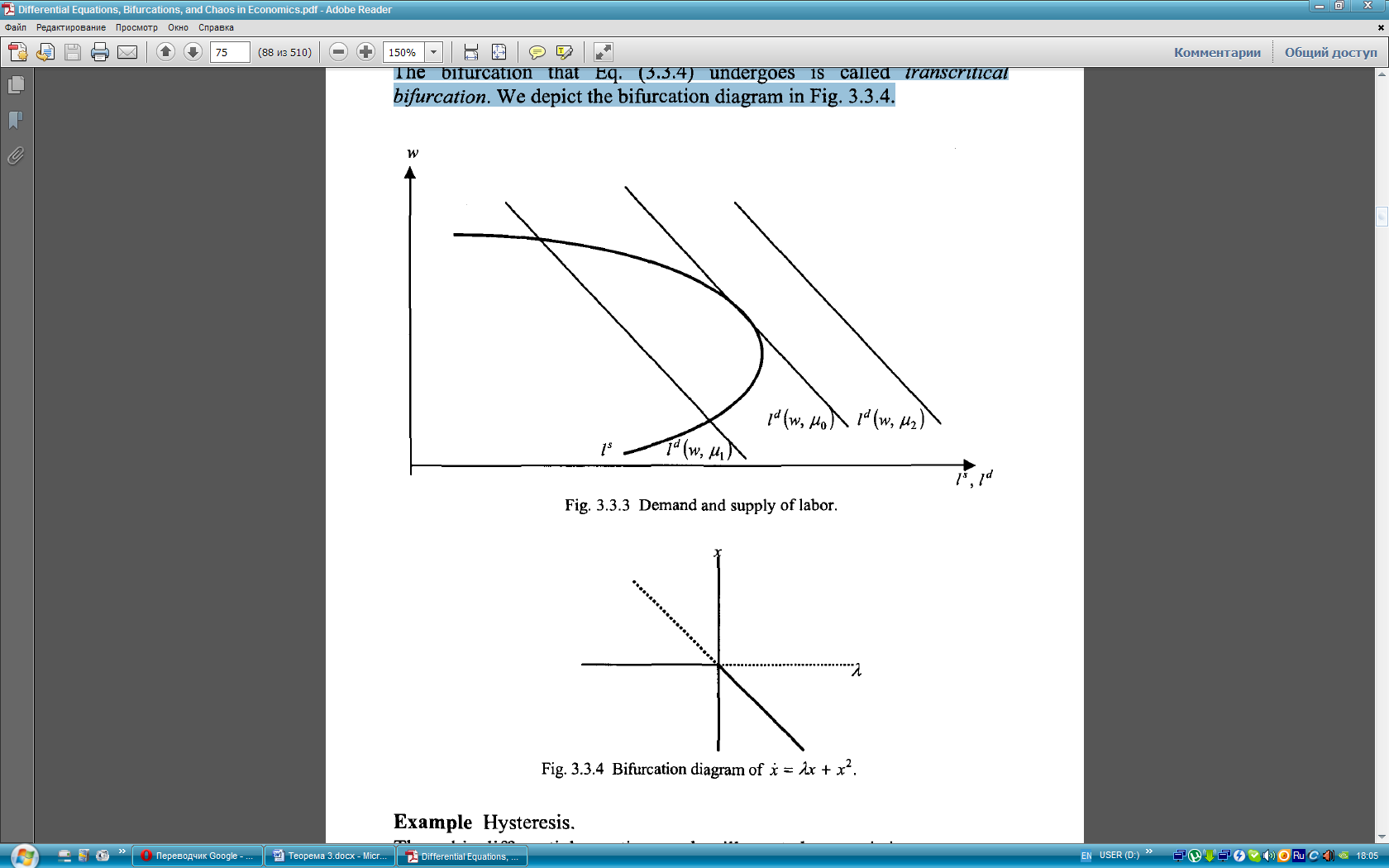
Пример Транскритические бифуркации.

Рассмотрим дифференциальное уравнение

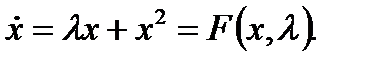(3.3.4)

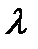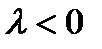Начало координат – точка равновесия для всех значений . Для начало координат асимптотически стабильно и существует другая точка равновесия 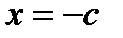, которая неустойчива. Значение параметра 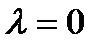- бифуркационное значение, при котором два равновесия сливаются в начале координат, которое есть нестабильной негиперболической точкой равновесия. Для 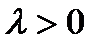начало координат нестабильно и существует другая точка равновесия 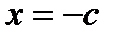, которая стабильна. Бифуркация, показанная в уравнении (3.3.4), называется транскритической бифуркацией. Изобразим данную бифуркацию на графике 3.3.4.

Пример Гистерезис.

Чтобы продемонстрировать гистерезис, используем кубическое дифференциальное уравнение

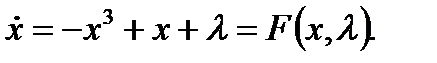(3.3.5)

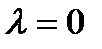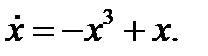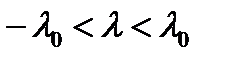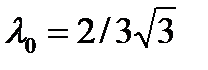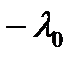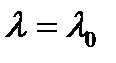При система имеет вид У нее три точки равновесия -1, 0, 1, и у нее стабильная орбитальная структура. Поток по-прежнему имеет стабильную орбитальную структуру при достаточно малых значениях параметра , где - локальное максимальное значение и - локальное минимальное значение . Для или 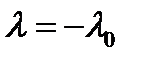, уравнение в точке бифуркации. Бифуркационный график показан на Рисунке 3.3.5. Бифуркация, описанная в уравнении (3.3.5), называется гистерезисом. Необходимо отметить, что система испытывает скачок при двух различных значениях параметров. Часть Рисунка (3.3.5), напоминающая параллелограмм, называется петлей гистерезиса.

Пример Бифуркация типа вил.

Рассмотрим

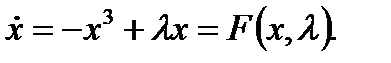(3.3.6)

При 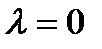, система имеет вид 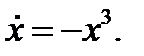Легко убедиться, что при любых положительных 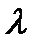уравнение (3.3.6) имеет три равновесия и стабильных орбитальных структуры. При 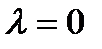, равновесия собираются в начале координат, и система находится в точке бифуркации. При всех , уравнение опять имеет стабильную орбитальную структуру. Бифуркация, показанная в уравнении (3.3.6), называется вилами бифуркации.

Для этого конкретного примера, бифуркация типа вил называется послекритической, потому что дополнительные точки равновесия, которые появляются в бифуркационном значении, имеют место для значений параметров, в которых точка равновесия нестабильна. Рисунок 3.3.6aизображает график послекритической бифуркации. Когда дополнительное равновесие происходит для значений параметра, при которых исходная точка равновесия устойчива, бифуркация называется докритической. Рисунок 3.3.6b демонстрирует докритическую бифуркацию вил для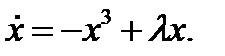

Пример Особенности исследования бифуркаций. (Cusp bifurcation)

Дифференциальное уравнение имеет вид

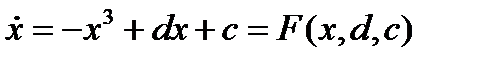, (3.3.7)

где 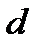и - реальные параметры. Векторное поле (3.3.7) является наиболее общим возмущением функции 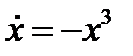при младших членах, т.к. любой член, включая 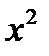, всегда может быть устранен разумным переводом переменной. В точках бифуркации дифференциальное уравнение должно иметь кратную точку равновесия, то есть 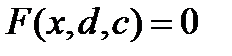и 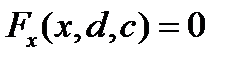. Для векторного поля (3.3.7) имеем

.

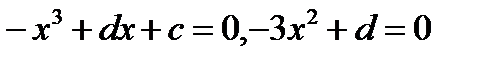Устранение 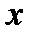из приведенных уравнений дает порог (касп (cusp))

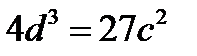(3.3.8)

Рисунок 3.3.7 изображает график 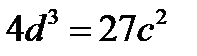в 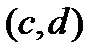-плоскости. В каждой соответствующей области плоскости 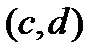, мы рисуем график функции 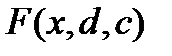и указываем поток, определяемый уравнением (3.3.7).

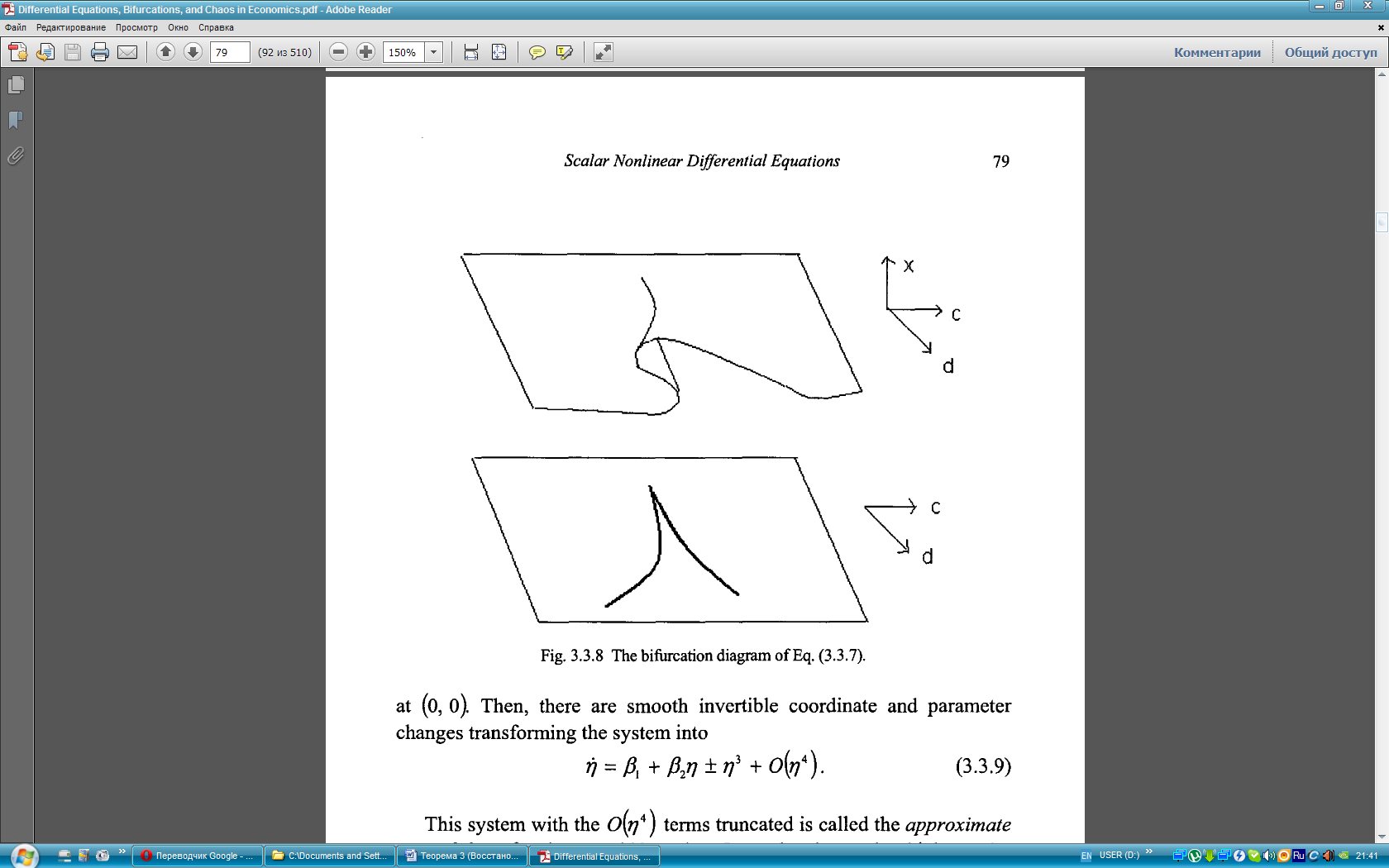
Полный бифуркационный график уравнения (3.3.7) в трехмерном 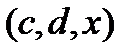-пространстве может быть построен из уравнения

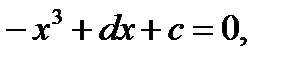
см. Рисунок 3.3.8.

Лемма 3.3.3 Предположим, что одномерная система

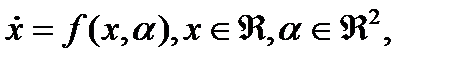
with smooth f, имеет в 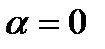равновесие 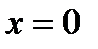, и пусть параболические условия бифуркации имеют вид

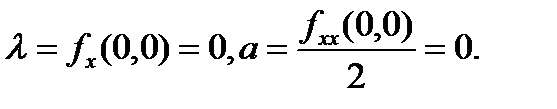
Предположим, что следующие условия типичности удовлетворены

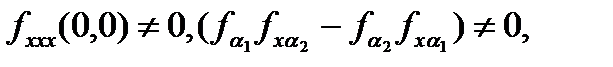
в (0,0). Затем, гладкие обратимые координаты и изменения параметра, трансформирующие систему в

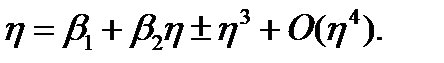(3.3.9)

Эта система с 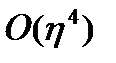усеченными членами называется приблизительной нормальной формой порога бифуркации. Можно показать, что члены высшего порядка на самом деле не изменяют их. Это называется

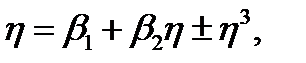
(3.3.10)

топологически нормальной формой для порога бифуркации. Можно доказать, что Уравнение (3.3.9) локально топологически эквивалентно в окрестности нуля Уравнению (3.3.10).

Теорема 3.3.2 (Топологически нормальная форма для порога бифуркации) Любая общая скалярная двухпараметрическая система 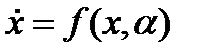имеет равновесие 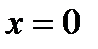в 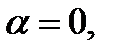экспонирующей порог бифуркации – локально топологически эквивалентна в окрестности нуля одной из нормальных форм (3.3.9).

Когда -мерная система имеет порог бифуркации, вышеуказанную теорему следует применять для уравнения на центральном многообразии. (См. главу 9).