Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пробне виконання завдання
|
|
Нехай дано функцію корисності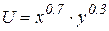 
.
Усі розрахунки та побудова графіків виконуються за допомогою програмного пакету “Mathematica”.
1. Вводимо функцію корисності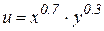 
. (
)
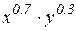2. Перевірте чи задовольняє функція корисності класичні властивості.
Перша умова: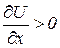 
та 
.
(
)
(
)
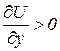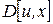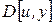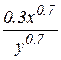Друга умова: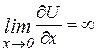 
, 
, 
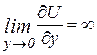
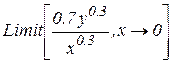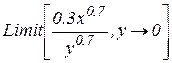
Третя умов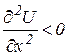а: 
та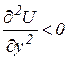 
.
(
)
(
)
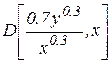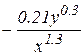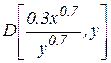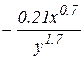Четверта умова: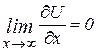 
, 
.
(
)
()
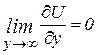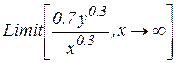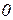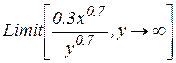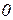3. Для заданої функції корисності будуємо функцію попиту споживача, тобто функцію Лагранжа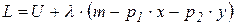 
. (
)
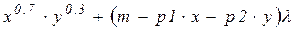Споживач завжди прагне максимізувати свою корисність. Щоб знайти безумовний екстремум функції Лагранжа, потрібно визначити похідні по x, y,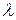 
.
(
)
(
)
(
)
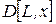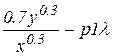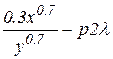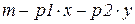Розв¢язуємо систему одержаних рівнянь.
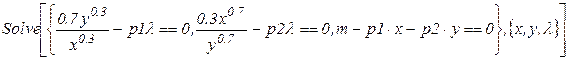
Серед розв¢язків вибираємо лише дійсні, у які підставляємо значення m=100,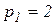 
, 
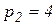. Визначаємо максимальну корисність (точка екстремуму).
(
)
(
)
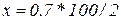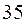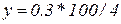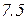Одержані значення підставляємо у функцію корисності і визначаємо максимальну корисність.
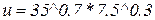
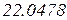
4. Будуємо криву байдужості, на якій корисність є величиною сталою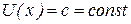 
. Нам потрібно побудувати графік залежності y від x.
ClearAll
(
)
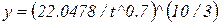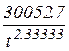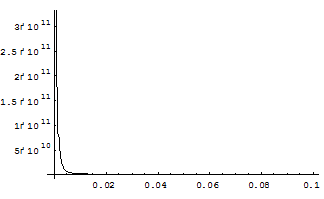
5. Визначаємо граничну норму заміщення другого товару першим в оптимальній точці,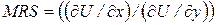 
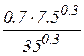(0.440957)
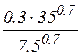(0.881914)
MRS=0.440957/0.881914 (0.5)
6. Будуємо поверхню, яку визначає задана функція корисності.
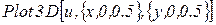
7. Самостійне виконання студентами індивідуальних завдань під контролем і за допомогою викладача. (30 хв.)
Завдання для індивідуальної роботи
1. U=2.9x^0.81y^0.22
2. U=3.7x^0.3y^0.7
3. U=3.9x^0.9y^0.1
4. U=3.2x^0.6y^0.4
5. U=1.3x^0.8y^0.2
6. U=3x^0.7y^0.3
7. U=2.1x^0.7y^0.3
8. U=0.8x^0.3y^0.7
9. U=1.7x^0.4y^0.6
10. U=2.5x^0.2y^0.8
11. U=1.5x^0.6y^0.4
12. U=0.5x^0.8y^0.2
13. U=2x^0.2y^0.8
14. U=1.9x^0.5y^0.5
15. U=0.9x^0.4y^0.6
16. U=1.2x^0.6y^0.4
17. U=3x^0.4y^0.6
18. U=2.3x^0.6y^0.4
19. U=2.7x^0.3y^0.7
20. U=2.9x^0.3y^0.7
21. U=1.4x^0.4y^0.6
22. U=3.9x^0.7y^0.3
23. U=1.1x^0.5y^0.5
24. U=2.2x^0.5y^0.5
8. Звіт студентів про роботу і теоретичне обгрунтування отриманих результатів. (10 хв.)
9. Підсумок заняття. (2 хв.)
Питання до групи:
1) Які властивості має функція корисності?
(
; 
; 
; 
)
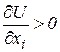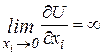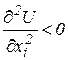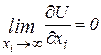2) Що називається граничною корисністю?
(
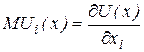- гранична корисність i -го товару.)
3) На що вказує норма заміщення? (Норма заміщення вказує, скільки необхідно одиниць другого товару, щоб замінити вибулу одиницю першого товару.
10. Домашнє завдання. (1 хв.)
Виконати розглянуті завдання для такої функції корисності: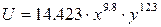 
.
«_______»__________________________2012 р.____________________________
(підпис практиканта)
Date: 2015-09-05; view: 353; Нарушение авторских прав