Симплексный метод

Симплексный метод (симплекс-метод) – метод последовательного улучшения решения ЗЛП, при котором целенаправленно перебирают опорные решения ЗЛП до тех пор, пока не будет найдено оптимальное.

Впервые симплекс-метод был предложен в 1947 г. американским математиком Джорджем Бернардом Данцингом, однако ещё в 1939 г. идеи этого метода прозвучали в работе российского учёного Л.В. Канторовича «Математические методы организации и планирования производства».

Алгоритм решения симплексным методом:

1) Привести ЗЛП к каноническому виду.

2) Найти начальное ОР. Если оно отсутствует, то ЗЛП не имеет решения в силу несовместности системы ограничений.

3) Проверить для ОР признак оптимальности. Если он выполняется, то оптимальное решение получено.

4) Проверить для ОР признак неограниченности целевой функции в ОДР. Если он выполняется, то оптимального решения не существует.

5) Выбрать базисную переменную. Если ЗЛП на максимум, то нужно выбрать любую свободную переменную с отрицательной оценкой (например, переменную с наименьшим номером). Если ЗЛП на минимум, то нужно выбрать любую свободную переменную с положительной оценкой (например, переменную с наибольшим номером). Выбранная свободная переменная будет базисной.

6) Выбрать уравнение, в котором заменяется базисная переменная. Номер l этого уравнения определяется по правилу минимума (6). Если минимум достигается сразу для нескольких номеров, то можно выбрать любое из них.

7) Перейти к новому ОР, используя при этом формулы (4) – (5) - правило прямоугольника и вернуться к выполнению пункта 3.

Поскольку число ОР конечно, то алгоритм закончит работу через конечное число шагов (оптимальное ОР будет получено при выполнении 2-го, 3-го или 4-го пунктов). Расчёты оформляются в симплекс-таблицы.

Пример 5. Решить симплекс-методом ЗЛП:

F (Х) = 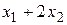→ max,

.

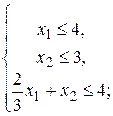
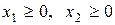Решение. Приведём ЗЛП к каноническому виду. Для этого введём дополнительные неотрицательные переменные х ₃, х ₄, х ₅ в систему ограничений:

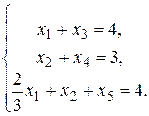
Расчёты представим в табл. 4, которая состоит из трёх частей, соответствующих выполнению трёх шагов симплекс-метода.

1 шаг. В первой части табл. 4 записаны коэффициенты при неизвестных и свободные члены системы ограничений канонической ЗЛП; базисные переменные - х ₃, х ₄, х ₅; свободные переменные - х ₁, х ₂. Во 2-м столбце записаны коэффициенты целевой функции при базисных переменных х ₃, х ₄, х ₅.

Число 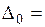0∙4 + 0∙3 + 0∙4 = 0 = F (Х) записано в последней строке последнего столбца первой части табл. 4.

;

.

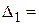
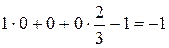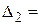
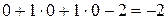Числа 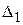, 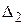записаны в последней строке первой части табл. 4 в столбцах, соответствующих свободным переменным х ₁, х ₂. Оценки базисных переменных х ₃, х ₄, х ₅ равны нулю.

Таблица 4

Базис		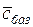					Свободные коэффициенты
х 1	х 2	х 3	х 4	х 5
х 3 х 4 х 5		2/3
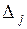
	-1	-2
х 3 х 2 х 5		2/3			-1
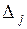
	-1
х 3 х 2 х 1					3/2 -3/2	-3/2 3/2	5/2 3/2
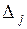
				1/2	3/2	15/2

По последнему столбцу записываем первое полученное ОР (0, 0, 4, 3, 4). Значение целевой функции F (0, 0, 4, 3, 4) = 0.

В строке оценок 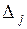получены два отрицательных числа, следовательно, ОР (0, 0, 4, 3, 4) не является оптимальным и может быть улучшено.

В качестве базисной переменной выбираем х ₂, т.к. ей соответствует наибольшая по абсолютной величине отрицательная оценка. Номер l опорной строки определяем по правилу минимума (6):

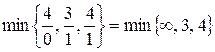= 3 .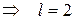

Во 2-й строке первой части табл. 14 базисная переменная х ₄ заменяется на х ₂. Опорный элемент таблицы d_lS = d₂₂ = 1 (выделен полужирным курсивом).

2 шаг. Во второй части табл. 4 базисные переменные - х ₃, х ₂, х ₅; свободные переменные - х ₁, х ₄.

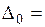0∙4 + 2∙3 + 0∙1 = 6 = F (Х);

;

.

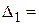
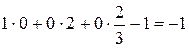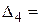
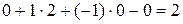По последнему столбцу записываем второе полученное ОР (0, 3, 4, 0, 1). Значение целевой функции F (0, 3, 4, 0, 1) = 6, видим, что оно улучшено.

В строке оценок 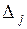получено одно отрицательное число, следовательно, ОР (0, 3, 4, 0, 1) также не является оптимальным и опять может быть улучшено.

В качестве базисной переменной выбираем х ₁, т.к. ей соответствует отрицательная оценка. Номер l опорной строки определяем по правилу минимума (6):

.

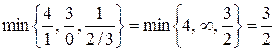
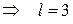В 3-й строке второй части табл. 14 базисная переменная х ₅ заменяется на х ₁. Опорный элемент таблицы d_lS = d ₃₁ = 2/3 (выделен полужирным курсивом).

3 шаг. В третьей части табл. 4 базисные переменные - х ₃, х ₂, х ₁; свободные переменные - х ₅, х ₄.

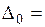
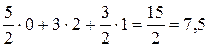= F (Х);

;

.

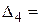
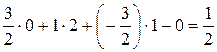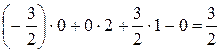По последнему столбцу записываем третье полученное ОР (3/2, 3, 5/2, 0, 0). Значение целевой функции F (3/2, 3, 5/2, 0, 0) = 7,5. Оно улучшено по сравнению с предыдущим.

В строке оценок 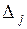получены неотрицательные числа, следовательно, ОР (3/2, 3, 5/2, 0, 0) является оптимальным.

Таким образом, на третьем шаге симплекс-метода получено единственное оптимальное решение для исходной ЗЛП: х ₁ = 1,5; х ₂ = 3.

.

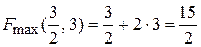Можно проверить правильность найденного оптимального решения графическим методом (рис. 2).

ОДР данной задачи – многоугольник OABCD. Нормальный вектор 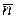= (1; 2). Перпендикулярно вектору 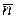строим линию уровня 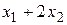= 0. Перемещаем её в направлении вектора 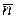до последней точки В, в которой она касается ОДР.

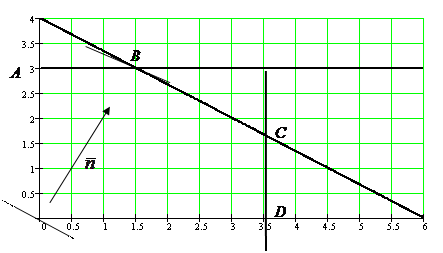Максимум достигается в вершине В (1,5; 3).

Рис. 2. Решение ЗЛП графическим методом

Пример 6. Решить симплекс-методом ЗЛП:

F (Х) = 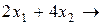max,

.

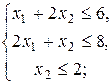
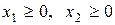Решение. Приведём ЗЛП к каноническому виду. Для этого введём дополнительные неотрицательные переменные х ₃, х ₄, х ₅ в систему ограничений:

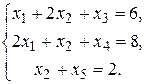
Расчёты представим в табл. 5, которая состоит из трёх частей, соответствующих выполнению трёх шагов симплекс-метода.

1 шаг. В первой части табл. 5 записаны коэффициенты при неизвестных и свободные члены системы ограничений канонической ЗЛП; базисные переменные - х ₃, х ₄, х ₅; свободные переменные - х ₁, х ₂. Во 2-м столбце записаны коэффициенты целевой функции при базисных переменных х ₃, х ₄, х ₅.

Число 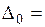0∙6 + 0∙8 + 0∙2 = 0 = F (Х) записано в последней строке последнего столбца первой части табл. 15.

,

.

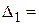
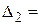
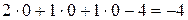Числа 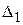, 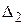записаны в последней строке первой части табл. 5 в столбцах, соответствующих свободным переменным х ₁, х ₂. Оценки базисных переменных х ₃, х ₄, х ₅ равны нулю.

Таблица 5

Базис		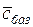					Свободные коэффициенты
х 1	х 2	х 3	х 4	х 5
х 3 х 4 х 5
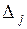
	- 2	- 4
х 3 х 4 х 2						- 2 - 1
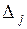
	- 2
х 1 х 4 х 2				- 2		- 2

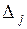
По последнему столбцу записываем первое полученное ОР (0, 0, 6, 8, 2). Значение целевой функции F (0, 0, 6, 8, 2) = 0.

В строке оценок 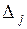получены два отрицательных числа, следовательно, ОР (0, 0, 6, 8, 2) не является оптимальным и может быть улучшено.

В качестве базисной переменной выбираем х ₂, т.к. ей соответствует наибольшая по абсолютной величине отрицательная оценка (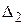 = - 4). Номер l опорной строки определяем по правилу минимума (6):

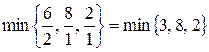= 2 .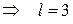

В 3-й строке первой части табл. 15 базисная переменная х ₅ заменяется на х ₂. Опорный элемент таблицы d_lS = d ₃₂ = 1 (выделен полужирным курсивом).

2 шаг. Во второй части табл. 5 базисные переменные - х ₃, х ₂, х ₄; свободные переменные - х ₁, х ₅.

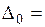0∙2 + 0∙6 + 4∙2 = 8 = F (Х),

,

.

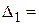
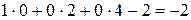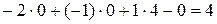По последнему столбцу записываем второе полученное ОР (0, 2, 2, 6, 0). Значение целевой функции F (0, 2, 2, 6, 0) = 8 улучшено.

В строке оценок 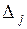получено одно отрицательное число 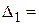- 2, следовательно, ОР (0, 2, 2, 6, 0) также не является оптимальным и опять может быть улучшено.

В качестве базисной переменной выбираем х ₁, т.к. ей соответствует отрицательная оценка. Номер l опорной строки определяем по правилу минимума (6):

.

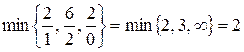
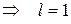В 1-й строке второй части табл. 5 базисная переменная х ₃ заменяется на х ₁. Опорный элемент таблицы d_lS = d ₁₁ = 1 (выделен полужирным курсивом).

3 шаг. В третьей части табл. 5 базисные переменные - х ₄, х ₂, х ₁; свободные переменные - х ₅, х ₃.

,

,

.

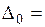
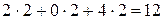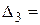
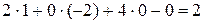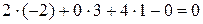По последнему столбцу записываем третье полученное ОР (2, 2, 0, 2, 0). Значение целевой функции F (2, 2, 0, 2, 0) = 12.

В строке оценок получены неотрицательные числа, следовательно, ОР (2, 2, 0, 2, 0) является оптимальным. Это одно из бесконечного множества оптимальных решений, т.к. оценка свободной переменной 0.

Date: 2015-09-20; view: 758; Нарушение авторских прав