Выражение целевой функции через свободные переменные

Оценки свободных переменных.

Рассмотрим каноническую ЗЛП, для которой система ограничений приведена к стандартному виду.

F (Х) = 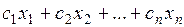→ max (min),

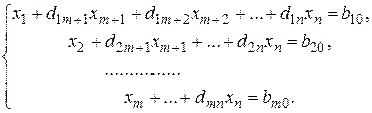
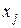≥ 0, j = 1, 2, …, n.

Выразим базисные переменные через свободные и подставим выражения (3) в целевую функцию.

F (Х) = = () +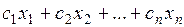

+ () + … + () + =

- + + … +

+ + + … + =

= .

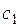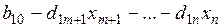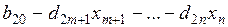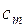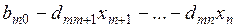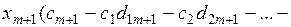
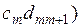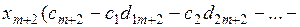
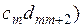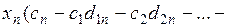
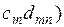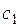
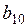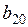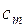
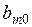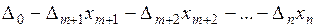Таким образом, получим

F (Х) = , (7)

где + + … + ;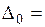

;

…………..

.

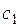
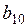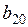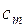
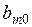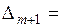
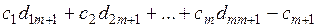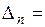
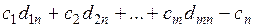Числа 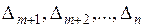называют оценками свободных переменных х_{m+ 1}, х _{m+ 2}, …, х_n.

Кратко выражение для оценки 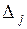можно записать так:

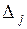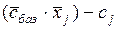= , (8)

где 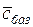= (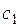, , …, 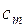) - вектор коэффициентов целевой функции при базисных переменных. В общем случае первая компонента этого вектора равна коэффициенту целевой функции при базисной переменной 1-го уравнения, 2-я компонента вектора 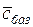- коэффициент целевой функции при базисной переменной 2-го уравнения, и т.д., последняя, m -я компонента вектора 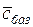- коэффициент целевой функции при базисной переменной m -го уравнения.

Вектор 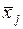= - это вектор коэффициентов при переменной х_j в системе (5.9).

Число 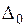- это скалярное произведение векторов 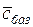и :

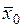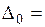
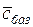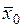∙ , (9)

где координаты вектора 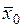= (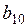, , 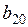…, 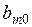) – правые части системы (2).

Число - это коэффициент при свободной переменной х_j в целевой функции. Заметим, что выражение (7) можно представить в виде

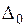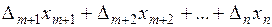= F + (10)

и рассматривать как ещё одно линейное уравнение, добавленное к системе (2). Оно ничем не отличается от остальных уравнений (2); его базисной переменной всегда является переменная F.

Новые значения оценок свободных переменных и число 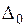можно пересчитывать по формулам:

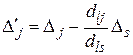, (11)

где 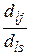- коэффициент при переменной х_j в l -м уравнении, который умножается на число (- d_is) для исключения из i -го уравнения переменной х_s;

j = 0, 1, 2, …, n.

Пример 4. Дана ЗЛП:

F (Х) = 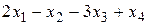→ max,

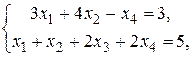
≥ 0, i = 1, 2, 3, 4.

Выразить целевую функцию через свободные переменные х ₂, х ₄.

Решение. Воспользуемся формулой (5.14) для записи целевой функции через свободные переменные х ₂, х ₄: F (Х) = .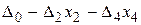

Расчёты оценок 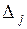и 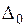представим в табл. 12. Такие таблицы называются симплексными (симплекс-таблицы).

Таблица 2

Базис		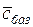2 -1 -3 1	Свободные коэффициенты
х 1	х 2	х 3	х 4
х 1 х 3	- 3		4/3 -1/6		-1/3 7/6
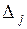
		25/6		- 31/6	- 4

В первой строке табл. 2 над неизвестными х ₁, х ₂, х ₃, х ₄ записаны соответствующие коэффициенты целевой функции.

Во 2-м столбце записаны коэффициенты целевой функции при базисных переменных х ₁, х ₃.

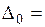
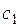
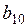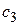
Число + 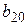= 2∙1 + (- 3)∙2 = - 4 записано в последней строке последнего столбца табл. 12.

= ,

= .

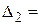
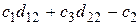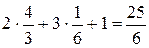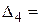
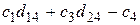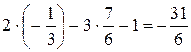Числа 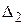, 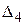записаны в последней строке табл. 2 в столбцах, соответствующих свободным переменным х ₂, х ₄. Оценки базисных переменных х ₁, х ₃ равны нулю, т.к. эти переменные исключаются из целевой функции.

Таким образом, целевая функция F (Х) = 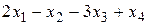может быть записана через свободные переменные х ₂, х ₄ следующим образом:

F (Х) = = .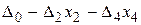

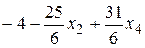Исследуем полученную целевую функцию. Для этого представим заданную ЗЛП в виде, когда целевая функция и базисные переменные выражены через свободные переменные х ₂, х ₄:

F (Х) = 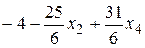→ max,

≥ 0, i = 1, 2, 3, 4.

Свободные переменные могут принимать любые значения, кроме тех, которые нарушают условие неотрицательности.

Пусть х ₂ = х ₄ = 0, тогда х ₁ = 1 > 0, х ₃ = 2 > 0, F (Х) = - 4 < 0, т.е. на опорном решении (1, 0, 2, 0) целевая функция отрицательна.

Исходя из условия ЗЛП F (Х) → max, появляется закономерный вопрос: «Каким образом можно увеличить значение целевой функции?».

Это можно сделать, если одну из свободных переменных оставить равной нулю (например, х ₂ = 0), а другую взять положительной (например, х ₄ > 0), тогда значение целевой функции F (Х) = 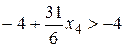, т.е. увеличилось.

Отметим, что увеличивать х ₄ беспредельно нельзя, поскольку при этом может нарушаться условие неотрицательности для переменных х ₁, х ₃.

Если х ₂ = 0, х ₄ ≠ 0, то базисные переменные можно представить так:

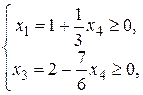
что равносильно ограничению для х ₄: 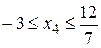. Откуда наибольшее возможное значение х ₄ = 12/7. Тогда

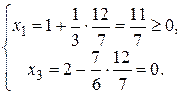
Следовательно, целевая функция F (Х) = 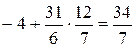на ОР (11/7, 0, 0, 12/7), где х ₁, х ₄ – базисные переменные, х ₂, х ₃ - свободные.

Преобразования сведены в табл. 3. Во 2-й строке первой части табл. 3 базисная переменная х ₃ заменяется на х ₄. Опорный элемент таблицы - d_lS = d₂₄ = 7/6 (выделен полужирным курсивом).

Таблица 3

Базис		2 -1 -3 1	Свободные коэффициенты
х 1	х 2	х 3	х 4
х 1 х 3	- 3		4/3 -1/6		-1/3 7/6
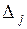
		25/6		- 31/6	- 4
х 1 х 4			9/7 -1/7	2/7 6/7		11/7 12/7
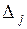
		24/7	31/7		34/7

Теперь целевая функция и базисные переменные х ₁, х ₄ выражаются через свободные переменные х ₂, х ₃ так:

F (Х) = ,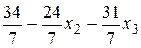

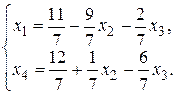
Можно ли дальше увеличивать значение целевой функции F (Х)? Ответ дают следующие признаки.

Date: 2015-09-20; view: 3226; Нарушение авторских прав