
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методом равных и наименьших относительных отклонений
|
|
Пусть необходимо найти компромиссное решение задачи линейной оптимизации, в которой имеется p > 1 линейных частных критериев вида
 ;
; 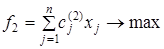 ; …;
; …; 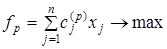 , (1)
, (1)
а система ограничений задается аналогично задаче линейного программирования следующим образом:
 (
(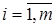 );
); 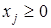 (
( ). (2)
). (2)
Обозначим через 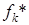 максимальное значение критерия
максимальное значение критерия 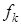 , полученное в результате решения задачи линейного программирования с единственной целевой функцией
, полученное в результате решения задачи линейного программирования с единственной целевой функцией 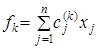 при ограничениях (2). Предположим, что
при ограничениях (2). Предположим, что 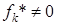 для всех
для всех 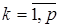 . Поскольку
. Поскольку 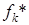 могут иметь разные знаки, то для удобства представим исходную задачу таким образом, чтобы значения всех частных критериев, полученные для каждого из них в отдельности без учета других, были бы положительными.
могут иметь разные знаки, то для удобства представим исходную задачу таким образом, чтобы значения всех частных критериев, полученные для каждого из них в отдельности без учета других, были бы положительными.
Разобьем все множество частных критериев F = { f 1, f 2, …, fp } на два непересекающихся подмножества  и
и 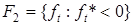 . Затем, сохраняя эквивалентность исходной задачи, введем новые частные критерии оптимальности:
. Затем, сохраняя эквивалентность исходной задачи, введем новые частные критерии оптимальности:
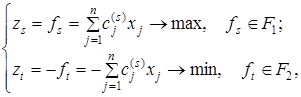 (3)
(3)
где их экстремальные значения 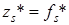 для
для 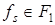 и
и 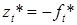 для
для  .
.
Тогда учитывая, что 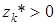 для всех
для всех 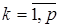 , условие равенства относительных отклонений значений частных критериев от их экстремальных значений можно записать как
, условие равенства относительных отклонений значений частных критериев от их экстремальных значений можно записать как
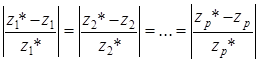 . (4)
. (4)
Выполним анализ условия (4) с целью исключения операции определения абсолютной величины. Для этого рассмотрим произвольную пару критериев 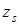 и
и 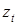 .
.
Пусть 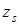 ,
, 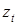 Î F 1, т.е. эти частные критерии максимизируются. Тогда
Î F 1, т.е. эти частные критерии максимизируются. Тогда
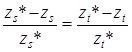 или
или 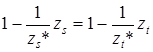 , (5)
, (5)
поскольку оба числителя 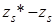 и
и  положительны. Обозначим
положительны. Обозначим 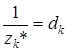 для всех
для всех 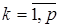 и подставим в (5). Это условие будет иметь вид:
и подставим в (5). Это условие будет иметь вид:
 или
или 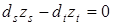 . (6)
. (6)
Если рассмотреть критерии 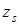 ,
, 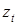 Î F 2, которые одновременно минимизируются, то получим точно такое же уравнение (6), так как направления их оптимизации также совпадают.
Î F 2, которые одновременно минимизируются, то получим точно такое же уравнение (6), так как направления их оптимизации также совпадают.
В том случае, когда 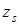 Î F 1,
Î F 1, 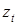 Î F 2 или
Î F 2 или 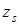 Î F 2,
Î F 2, 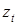 Î F 1, т.е. критерии
Î F 1, т.е. критерии 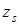 и
и 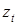 имеют разные направления оптимизации, получаем
имеют разные направления оптимизации, получаем
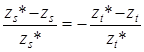
или с учетом введенных обозначений
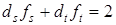 . (7)
. (7)
Таким образом, равенство относительных отклонений для любых двух частных критериев 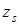 и
и 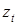 имеет вид (6), если направления их оптимизации совпадают, или (7), если они противоположны.
имеет вид (6), если направления их оптимизации совпадают, или (7), если они противоположны.
Чтобы получить компромиссное решение исходной многокритериальной задачи с ограничениями (2) и частными критериями оптимальности (3) методом равных и наименьших отклонений, необходимо решить расширенную задачу линейного программирования, которая формулируется следующим образом.
Шаг 1. Дополнительно к переменным 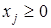 (
( ) исходной задачи вводятся неотрицательные переменные
) исходной задачи вводятся неотрицательные переменные 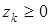 (
(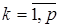 ).
).
Шаг 2. В качестве целевой функции выбирается один любой частный критерий оптимальности, например, z 1 Î F 1, где
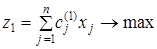 . (8)
. (8)
Шаг 3. В систему ограничений вводятся p дополнительных уравнений, определяющих возможные значения переменных 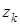 (
(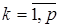 ):
):
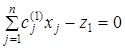 ;
; 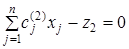 ; …;
; …; 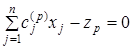 . (9)
. (9)
Шаг 4. В систему ограничений вводятся p -1 дополнительных уравнений, устанавливающих равенство относительных отклонений частных критериев от их экстремальных значений:
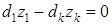 ,
,  (10)
(10)
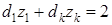 ,
, 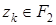 . (11)
. (11)
Если частный критерий zk имеет такое же направление оптимизации, что и целевая функция (8), т.е. критерий z 1, то добавляется ограничение (10), если противоположное, то ограничение (11).
Таким образом, компромиссное решение задачи многокритериальной линейной оптимизации можно получить, если решить расширенную задачу линейного программирования с целевой функцией (8) и ограничениями (2), (9)-(11) при условии неотрицательности всех переменных. При этом нетрудно заметить, что с учетом условия (4), максимизация целевой функции z 1 7обеспечивает минимизацию относительных отклонений всех частных критериев от их экстремальных значений.
Замечание. Если необходимо улучшить значения каких-то критериев, то в условие (4) вводятся весовые коэффициенты b2, b3,…, b p, где b1 = 1, учитывающие важность частных критериев относительно целевой функции z 1:
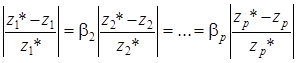 .
.
Тогда условие, соответствующее ограничению (10), будет иметь вид
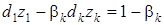 , (12)
, (12)
а для ограничения (11) оно запишется как
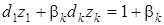 . (13)
. (13)
Пример. Требуется найти компромиссное решение задачи линейной оптимизации с тремя частными критериями
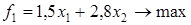 ;
; 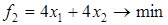 ;
; 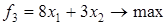 ,
,
область допустимых решений в которой задается ограничениями
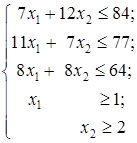
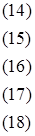
при условии неотрицательности всех переменных.
Найдем решение задачи по каждому из критериев в отдельности. Воспользуемся для этого средствами программы Excel. Исходные данные, записанные на рабочем листе электронной таблицы, показаны на рис. 1.
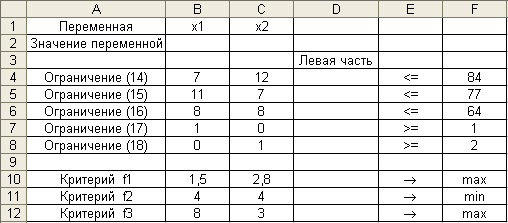
Рис. 1
Чтобы определить ограничения задачи и частные критерии оптимальности, в соответствующих ячейках требуется задать формулы, приведенные в таблице 1.
Таблица 1
| Ячейка | Формула |
| D4 | =СУММПРОИЗВ(В4:С4; $B$2:$С$2) |
| D5 | =СУММПРОИЗВ(В5:С5; $B$2:$С$2) |
| D6 | =СУММПРОИЗВ(В6:С6; $B$2:$С$2) |
| D7 | =СУММПРОИЗВ(В7:С7; $B$2:$С$2) |
| D8 | =СУММПРОИЗВ(В8:С8; $B$2:$С$2) |
| D10 | =СУММПРОИЗВ(В10:С10; $B$2:$С$2) |
| D11 | =СУММПРОИЗВ(В11:С11; $B$2:$С$2) |
| D12 | =СУММПРОИЗВ(В12:С12; $B$2:$С$2) |
Для решения задачи по каждому из критериев необходимо в диалоговом окне «Поиск решения » указать адрес целевой ячейки (D10, D11 или D12), направление оптимизации, ввести ограничения, задать параметры (Линейная модель и Неотрицательные значения) и нажать кнопку Выполнить.
Результаты поиска решения по критерию f 1 показаны на рис. 2, по критерию f 2 на рис. 3 и по критерию f 3 на рис. 4.
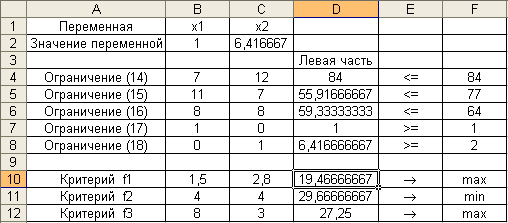
Рис. 2

Рис. 3
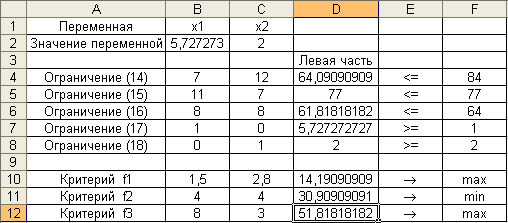
Рис. 4
В таблице 2 представлены значения переменных и частных критериев оптимальности, полученные при решении задачи по каждому критерию в отдельности. Очевидно, что критерии имеют противоречивый характер, так как значение каждого из них ухудшается, если решение выполняется по одному из других критериев.
Таблица 2
| Критерий решения | Полученные результаты | ||||
| Переменные | Значения критериев | ||||
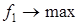
| x 1 = 1,000 | x 2 = 6,417 | 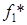 = 19,467 = 19,467
| 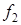 = 29,667 = 29,667
| 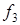 = 27,250 = 27,250
|
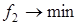
| x 1 = 1,000 | x 2 = 2,000 | 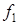 = 7,100 = 7,100
| 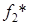 = 12,000 = 12,000
| 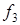 = 14,000 = 14,000
|
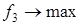
| x 1 = 5,727 | x 2 = 2,000 | 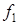 = 14,191 = 14,191
| 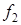 = 30,909 = 30,909
| 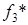 = 51,818 = 51,818
|
Далее найдем компромиссное решение задачи методом равных и наименьших отклонений. Поскольку все значения 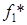 ,
, 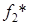 ,
, 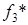 положительны, то
положительны, то 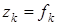 , причем
, причем 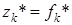 , где
, где 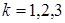 , и
, и
 ;
; 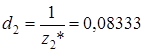 ;
; 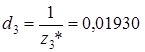 .
.
В качестве целевой функции расширенной задачи выберем первый частный критерий оптимальности
 .
.
Тогда дополнительные ограничения будут иметь следующий вид:
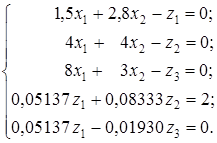

Расположение исходных данных на рабочем листе электронной таблицы показано на рис. 5.
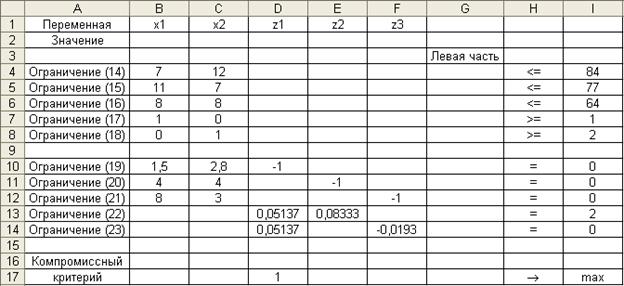
Рис. 5
Используемые для расчетов формулы и адреса соответствующих ячеек даны в таблице 3. Значение целевой функции находится в ячейке G17, изменяемые переменные размещены в диапазоне B2:F2.
Таблица 3
| Ячейка | Формула |
| G4 | =СУММПРОИЗВ(В4:F4; $B$2:$F$2) |
| G5 | =СУММПРОИЗВ(В5:F5; $B$2:$F$2) |
| G6 | =СУММПРОИЗВ(В6:F6; $B$2:$F$2) |
| G7 | =СУММПРОИЗВ(В7:F7; $B$2:$F$2) |
| G8 | =СУММПРОИЗВ(В8:F8; $B$2:$F$2) |
| G10 | =СУММПРОИЗВ(В10:F10; $B$2:$F$2) |
| G11 | =СУММПРОИЗВ(В11:F11; $B$2:$F$2) |
| G12 | =СУММПРОИЗВ(В12:F12; $B$2:$F$2) |
| G13 | =СУММПРОИЗВ(В13:F13; $B$2:$F$2) |
| G14 | =СУММПРОИЗВ(В14:F14; $B$2:$F$2) |
| G17 | =СУММПРОИЗВ(В17:F17; $B$2:$F$2) |
Для получения компромиссного решения задачи в диалоговом окне «Поиск решения » указывается адрес целевой ячейки G17, направление оптимизации (для критерия z 1 это максимальное значение), указываются ограничения и задаются параметры Линейная модель и Неотрицательные значения. Состояние ячеек электронной таблицы после выполнения поиска решения показано на рис. 6.
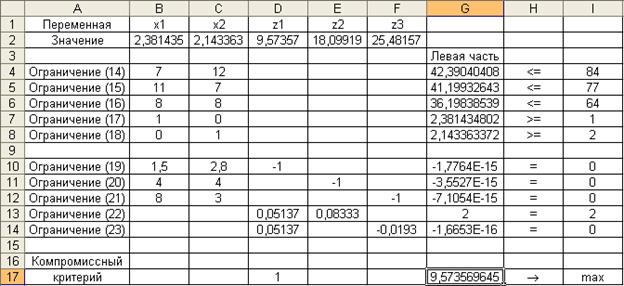
Рис. 6
Компромиссное решение, полученное по методу равных и наименьших относительных отклонений, имеет следующий вид:
x 1 = 2,38; x 2 = 2,14; f 1 = z 1 = 9,57; f 2 = z 2 = 18,10; f 3 = z 3 = 25,48.
Относительные отклонения частных критериев от их экстремальных значений удовлетворяют условию:
 .
.
В компромиссном решении количественные значения частных критериев существенно отличаются от их экстремальных значений (таблица 2). Чтобы изменить их количественное соотношение, т.е. улучшить (ухудшить) некоторые частные критерии за счет ухудшения (улучшения) других, введем весовые коэффициенты для их относительных отклонений.
Пусть b1 = 1, b2 = 0,5 и b3 = 1. Это означает, что критерий f 2 = z 2 является менее важным и может быть ухудшен по сравнению с другими показателями оптимальности. Тогда для получения компромиссного решения дополнительное ограничение (22), определяющее равенство отклонений первого и второго критериев, следует заменить следующим ограничением, полученным по формуле (13):
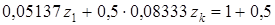 .
.
Окончательно оно принимает следующий вид:
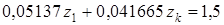 .
.
Рабочий лист электронной таблицы для поиска компромиссного решения с учетом введенных весовых коэффициентов приведен на рис. 7.
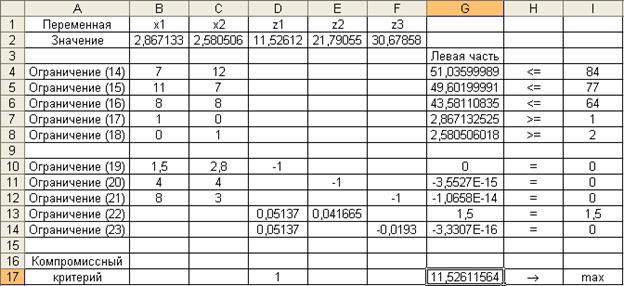
Рис. 7
Полученные результаты показывают, что значения первого и третьего критериев улучшились за счет ухудшения второго критерия:
x 1 = 2,87; x 2 = 2,58; f 1 = z 1 = 11,53; f 2 = z 2 = 21,79; f 3 = z 3 = 30,69.
Замечание. Область допустимых решений задачи, определяемая ограничениями (14)-(18), представляет собой выпуклый многоугольник, расположенный в неотрицательной области координатной плоскости. Решения, полученные по каждому частному критерию в отдельности (таблица 2) соответствуют допустимым базисным решениям задачи линейного программирования и располагаются в вершинах этого многоугольника. Компромиссное решение, как правило, определяется точкой, расположенной внутри этого многоугольника.
Date: 2015-09-19; view: 2535; Нарушение авторских прав