
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определить координаты точки на топографической карте
|
|
Линии, соединяющие одинаковые по широте точки земной поверхности, называют параллелями. Линии, соединяющие одинаковые по долготе точки земной поверхности, называют меридианами. Меридианы и параллели являются рамками листов топографических карт.
Географические координаты на карте определяют по рамкам листа (рис. 11), подписанным в углах, и залитым штрихам (минутным делениям). Например, на нашем рисунке западная рамка листа карты (меридиан) имеет долготу 14° 00', южная рамка (параллель) имеет широту 54°15'. Географические координаты даются через одну минуту на рамках карт масштабом от 1:10 000 до 1: 200 000 и через 5 минут на рамках карт масштабом 1: 500 000 и 1: 1 000 000.
Для определения географических координат точки на карте (например, точки Б на рис. 11) необходимо провести меридиан и параллель через концы ближайших к точке одноминутных делений рамки. В нашем примере проведенный меридиан имеет долготу 14° 01', а проведенная параллель имеет широту 54° 16'. Затем оценивают на глаз или измеряют доли минуты по долготе и широте до интересующей нас точки и добавляют их к основным отсчетам. В результате широта точки Б равна 54° 16', 3, долгота - 14° 01’, 4.
Географическими координатами обычно пользуются при определении положения точек, удаленных одна от другой на значительные расстояния.
Юго-западная часть листа карты масштаба 1: 25 000
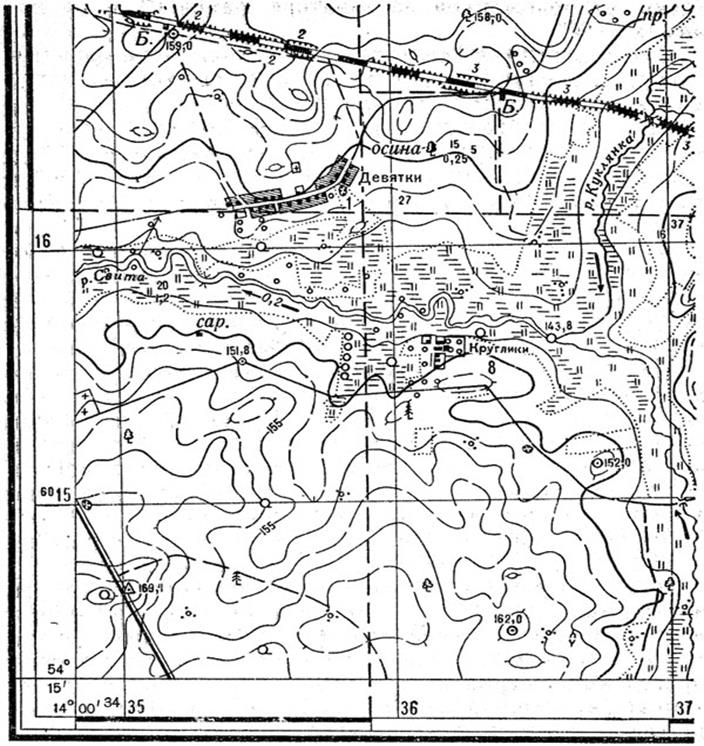
рис. 11
Под плоскими прямоугольными координатами понимают линейные величины, характеризующие относительное положение точки на плоскости. Поясним сущность их на рис. 12.
Плоские прямоугольные координаты
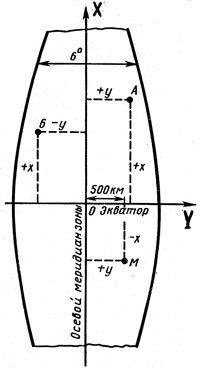
рис.12
Пусть на плоскости проведены две взаимно перпендикулярные линии, одна из которых проходит в вертикальном, а вторая (У) в горизонтальном направлении. Назовем эти линии осями координат, а точку их пересечения О - началом координат. Тогда положение любой точки на плоскости в данной системе координат относительно начала координат будет определяться кратчайшими расстояниями до нее от осей координат. Эти расстояния в виде прямых линий, перпендикулярных к одной из координатных осей и параллельных другой, являются координатами точек (х и у). Ось Х-ов принято также называть осью абсцисс, а ось У-ов - осью ординат. Из рис. 12 видно, что в зависимости от положения точки по отношению к осям координат ее абсцисса и ордината могут иметь положительные и отрицательные значения.
9. Что такое дирекционный угол и румб? Их взаимосвязь.
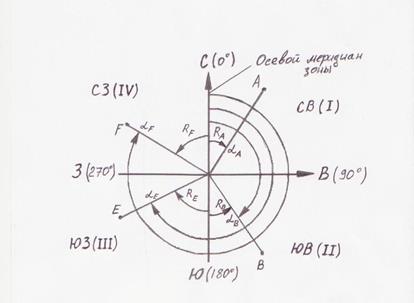
рис.13
Дирекционный угол (альфа) – двугранный угол между северным направлением оси координат до направления на данную точку отсчитанный по ходу часовой стрелки. Изменяется от 0° до 360°(см. рис. 13).
Румб (R) - двугранный угол, который откладывается как от северного так и от южного направления осей координат до направления на данную точку как по ходу часовой стрелки так и против часовой стрелки. Изменяется от 0° до 90°(см. рис. 13).
Взаимосвязь.
I четверть (СВ) - от 0° до 90° 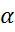 1=R1
1=R1
II четверть (ЮВ) - от 90° до 180° 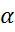 2=180°-R2
2=180°-R2
III четверть (ЮЗ) - от 180° до 270° 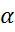 3=180°+R3
3=180°+R3
IV четверть (СЗ) - от 270° до 360° 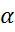 4=360°-R4
4=360°-R4
Date: 2015-09-19; view: 992; Нарушение авторских прав