
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод Эйлера. Методические указанияи задания к выполнению
|
|
Кафедра математики
Методические указанияи задания к выполнению
расчетно-графической работы по теме:
"Приближенные методы решения
дифференциальных уравнений"
для всех направлений подготовки бакалавров очной формы обучения
Брянск 2011
Брянская государственная инженерно-технологическая академия
Кафедра математики
Утверждены научно-методическим
советом БГИТА
Протокол №____от «___»_________2011 года
Методические указанияи задания к выполнению
расчетно-графической работы по теме:
"Приближенные методы решения
дифференциальных уравнений"
для студентов всех направлений подготовки бакалавров очной формы обучения всех специальностей
Брянск 2011
Составители: ст. преподаватель Тайц В.И.,
доцент Камозина О.В.,
доцент Котова И.А.
Рецензент: профессор кафедры Э и АПП, д. ф.-м. наук О.Г. Тайц
Рекомендованы редакционно-издательской и методической комиссиями механико-технологического факультета БГИТА.
Протокол №__________от «____»____________2011 г.
Приближенные методы решения дифференциальных уравнений
Решение многих дифференциальных уравнений нельзя свести к интегрированию известных функций. Поэтому важное значение приобретают приближенные методы решения.
Существуют два метода численного решения дифференциальных уравнений 1-го порядка: метод Эйлера и метод Рунге-Кутта.
Метод Эйлера
Для данного уравнения 1-го порядка
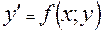 (1)
(1) 
можно составить таблицу приближенных значений частного решения, удовлетворяющего начальному условию
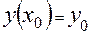 (2)
(2)
или приближенно вычертить интегральную кривую на некотором отрезке[ 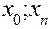 ].
]. 
По методу Эйлера данный отрезок [ 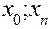 ] разбивается точками
] разбивается точками 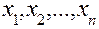 на n частичных отрезков.
на n частичных отрезков.
На первом частичном отрезке [ 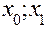 ] искомая интегральная кривая, проходящая через известную точку M0(
] искомая интегральная кривая, проходящая через известную точку M0(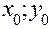 ) заменяется касательной к ней в точке
) заменяется касательной к ней в точке 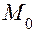
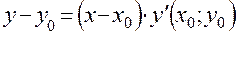 ,
,
Откуда при 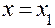 получается приближенное значение
получается приближенное значение 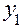 искомого решения уравнения в точке
искомого решения уравнения в точке 
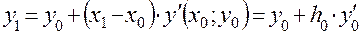 .
.
Далее тем же способом для отрезка [ 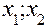 ] находим приближенное значение
] находим приближенное значение 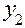 искомого решения в точке
искомого решения в точке 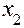
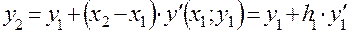 .
.
Продолжая этот процесс, последовательно находим приближенные значения 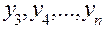 искомого решения в точках
искомого решения в точках 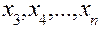 .
.
С увеличением 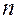 , при достаточно малой длине частичных отрезков, этим методом можно достигнуть заданной точности решения.
, при достаточно малой длине частичных отрезков, этим методом можно достигнуть заданной точности решения.
Данный отрезок [ 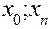 ] удобно разделить на частичные отрезки одинаковой длины
] удобно разделить на частичные отрезки одинаковой длины
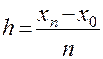 (шаг).
(шаг).
Тогда все последовательные приближенные значения 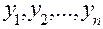 решения уравнения (1),удовлетворяющего начальному условию (2), вычисляются по рекуррентной формуле
решения уравнения (1),удовлетворяющего начальному условию (2), вычисляются по рекуррентной формуле
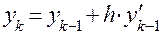 .
.
Таким образом, по методу Эйлера интегральную кривую, проходящую через точку 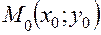 , заменяют ломаной (ломаной Эйлера), каждый отрезок которой проведен по направлению поля, определенного уравнением (1).Иными словами, от предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведенной через начальную точку каждого отрезка.
, заменяют ломаной (ломаной Эйлера), каждый отрезок которой проведен по направлению поля, определенного уравнением (1).Иными словами, от предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведенной через начальную точку каждого отрезка.
Недостатки метода Эйлера:
1. Малая точность при значительном шаге 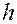 и большой объем работ при малом шаге.
и большой объем работ при малом шаге.
2. Систематическое накопление ошибок.
Поэтому метод Эйлера применяют лишь для грубых приближений.
Расчет ведется по следующей схеме:
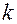
| 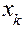
| 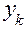
| 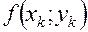
| 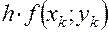
|
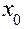
| 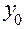
| 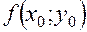
| 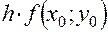
| |
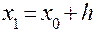
| 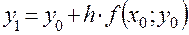
| 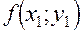
| 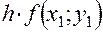
| |
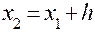
| 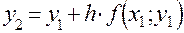
| 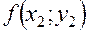
| 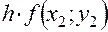
| |
| … | … | … | … | … |
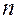 -1 -1
| 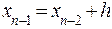
|  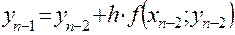
| 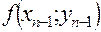
| 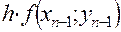
|
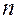
| 
| 
|
Date: 2015-09-19; view: 313; Нарушение авторских прав