
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Занятие 9. Дисперсионный анализ-продолжение
|
|

Двухфакторный анализ.

Нулевая и альтернативная гипотезы те же, что и при анализе однофакторного комплекса.
Нулевая гипотеза:  1 =
1 =  2 =
2 =  3 =...
3 =...  6 =
6 =  , (т.е. различия между выборочными средними рядов случайны).
, (т.е. различия между выборочными средними рядов случайны).
Альтернативная гипотеза: средняя выборочная хотя бы одной выборки отличается от генеральной средней.

Условия корректности проведения процедуры дисперсионного анализа также не меняются: случайность выборок, нормальность распределения вариант в выборках, отсутствие значимых различий между выборочными дисперсиями, независимость средней от вариансы в выборках.
 Если соблюдается условие аддитивности компонент вариансы всего комплекса, то общая сумма квадратов отклонений вариант от генеральной средней в двухфакторном комплексе разлагается следующим образом:
Если соблюдается условие аддитивности компонент вариансы всего комплекса, то общая сумма квадратов отклонений вариант от генеральной средней в двухфакторном комплексе разлагается следующим образом:  . Однако это обстоятельство ввиду случайности варьирования величин анализируемого показателя не соблюдается практически никогда.
. Однако это обстоятельство ввиду случайности варьирования величин анализируемого показателя не соблюдается практически никогда.




Поэтому обычно проверяют полную раскладку общего квадрата:

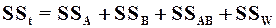 , где SSA - межгрупповая (факториальная) сумма квадратов, обусловленная различиями между выборками градаций фактора А, SSB - межгрупповая (факториальная) сумма квадратов, обусловленная различиями между выборками градаций фактора B, SSАB - сумма квадратов, обусловленная эффектами совместного воздействия факторов, а SSW - внутригрупповая (остаточная, необъясненная) сумма квадратов, обусловлена варьированием признака внутри отдельных выборок.
, где SSA - межгрупповая (факториальная) сумма квадратов, обусловленная различиями между выборками градаций фактора А, SSB - межгрупповая (факториальная) сумма квадратов, обусловленная различиями между выборками градаций фактора B, SSАB - сумма квадратов, обусловленная эффектами совместного воздействия факторов, а SSW - внутригрупповая (остаточная, необъясненная) сумма квадратов, обусловлена варьированием признака внутри отдельных выборок.
Далее каждую из них необходимо связать с соответствующей степенью свободы, т.е. определить средние квадраты отклонений. Расчет проводится по следующей схеме.
(Презентация с расчетами/без)
Ход анализа:
1.Расчет соответствующих сумм квадратов отклонений:
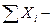 сумма вариант в ячейке дисперсионного комплекса;
сумма вариант в ячейке дисперсионного комплекса; 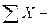 общая сумма вариант комплекса;
общая сумма вариант комплекса; 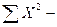 общая сумма квадратов вариант комплекса; N – объем комплекса; ni – число вариант в каждой ячейке, a – число градаций по фактору А; b – число градаций по фактору B.
общая сумма квадратов вариант комплекса; N – объем комплекса; ni – число вариант в каждой ячейке, a – число градаций по фактору А; b – число градаций по фактору B.
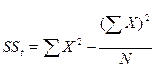 , где
, где 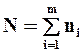
 |

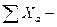 сумма вариант по каждой градации фактора А; na – число вариант по каждой градации фактора А.
сумма вариант по каждой градации фактора А; na – число вариант по каждой градации фактора А.

где  сумма вариант по каждой градации фактора В; nb – число вариант по каждой градации фактора В.
сумма вариант по каждой градации фактора В; nb – число вариант по каждой градации фактора В.
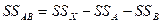
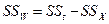
2. Расчет числа степеней свободы и дисперсий:
 | 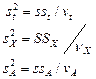 | |||||||||||
 | ||||||||||||
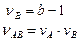 | ||||||||||||
 | ||||||||||||
 | ||||||||||||
 | ||||||||||||
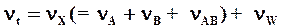 .
.
3. Оценка F-статистики и сравнение с критическим значением одностороннего F-критерия для выбранного уровня значимости (показаны условия принятия альтернативной гипотезы):
 ³
³ 
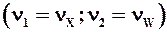
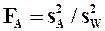 ³
³ 

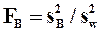 ³
³ 
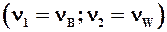
 ³
³ 

Если условие (в различных сочетаниях) соблюдается, то следует признать, что примененная организация комплекса обуславливает достоверную неоднородность сравниваемых выборок.
Пример. Изучалось влияние солености и глубины на распределение плотности моллюсков Macoma calcarea (Таблица 1). Для этого в акватории с соленостью 16 г/л на 6 станциях на глубинах от 0.5 до 3 м взяли по 5 выборочных площадок площадью 0.1 м2, в каждой из которых посчитали количество моллюсков (табл. 9). Аналогичную съемку осуществили в акватории с соленостью 24 г/л. Таким образом, был создан двухфакторный равномерный (в каждой ячейке по 5 вариант) дисперсионный комплекс: фактор А – глубина, число градаций по фактору А (а) равно 6, фактор В – соленость, число градаций по фактору (b) равно 2. Предположим, что соблюдаются все условия корректности проведения дисперсионного анализа.
Таблица 1.
| соленость | показатели | Глубина, м | |||||
| 0.5 | 1.5 | 2.5 | |||||
| 16 г/л | xi | ||||||
| åxi | |||||||
| 24 г/л | xi | ||||||
| åxi |
Нулевая гипотеза:  1 =
1 =  2 =
2 =  3 =...
3 =...  6 =
6 =  , (т.е. различия между выборочными средними рядов случайны).
, (т.е. различия между выборочными средними рядов случайны).
Альтернативная гипотеза: средняя выборочная хотя бы одной выборки отличается от генеральной средней.
Основой для анализа примем следующую раскладку общего квадрата отклонений:

Соответствующие суммы квадратов отклонений равны:
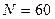 ;
;  ;
; 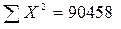 ; ni=5; a=6; b=2; na=10; nb=30
; ni=5; a=6; b=2; na=10; nb=30

SSx= 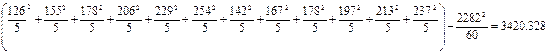
SSA= 
ssВ= 
SSAB=3420.328-3317.734-3.266=99.328
SSw=3665,933-3420.328=245,605
Соответствующие числа степеней свободы и дисперсии равны:
nt=N-1=60-1=59 
nA=a-1=6-1=5 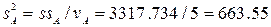
nB=b-1=2-1=1 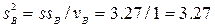
nAB= 
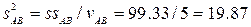
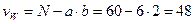
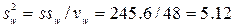
Затем рассчитаем величины F-статистики и сравним их с критическими значениями одностороннего F-критерия для выбранного уровня значимости:
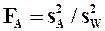 =663.55/5.12= 129.68 >
=663.55/5.12= 129.68 > 
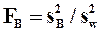 =3.27/5.12=0.64 <
=3.27/5.12=0.64 < 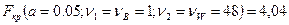
 =19.87/5.12=3.88 >
=19.87/5.12=3.88 > 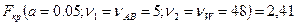
На данном уровне значимости нулевая гипотеза отвергается при сравнении выборок с разных глубин и при анализе совместного влияния глубины и солености. Не выявлено достоверной неоднородности анализируемого комплекса, обусловленной влиянием на исследуемый признак (плотность моллюсков) солености.
2. Двухфакторный дисперсионный анализ с помощью приложения «Анализ данных» в Microsoft Excel
Для проведения двухфакторного дисперсионного анализа также можно воспользоваться приложением «Анализ данных» в Microsoft Excel.
Выбираем раздел меню «Данные»-«Анализ данных»-«Двухфакторный дисперсионный анализ с повторениями» (Рис. 1).
|

В появившимся окне указываем диапазон ячеек с данными по всем выборкам («Входной интервал»). Диапазон ячеек выделяем вместе с названием столбцов (градации фактора А) и названием строк (градации фактора В). В окошке «Число строк для выборки» указываем объем отдельной выборки (в нашем случае 5), как показано на Рис. 2. Нажимаем «ОК» и получаем две таблицы с результатами (Таблица 2)
|
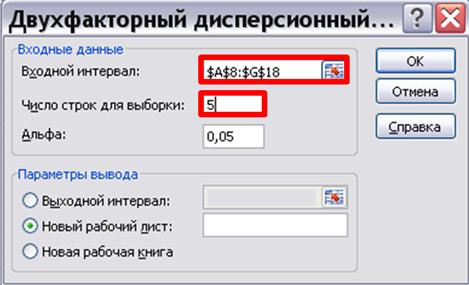
Табл. 2. Итоги двухфакторного дисперсионного анализа, проведенного с помощью "Анализа данных".
Двухфакторный дисперсионный анализ с повторениями
| ИТОГИ | 0,5 | 1,5 | 2,5 | Итого | |||
| Счет | |||||||
| Сумма | |||||||
| Среднее | 25,2 | 35,6 | 41,2 | 45,8 | 50,8 | 38,26667 | |
| Дисперсия | 14,7 | 4,3 | 8,7 | 2,2 | 3,7 | 83,44368 | |
| Счет | |||||||
| Сумма | |||||||
| Среднее | 28,4 | 33,4 | 35,6 | 39,4 | 42,6 | 47,4 | 37,8 |
| Дисперсия | 4,3 | 3,8 | 5,3 | 3,3 | 2,3 | 3,8 | 42,85517 |
| Итого | |||||||
| Счет | |||||||
| Сумма | |||||||
| Среднее | 26,8 | 32,2 | 35,6 | 40,3 | 44,2 | 49,1 | |
| Дисперсия | 11,28889 | 5,511111 | 4,266667 | 6,233333 | 4,844444 | 6,544444 | |
| Дисперсионный анализ | |||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое | |
| Выборка | 3,266667 | 3,266667 | 0,638436 | 0,428214 | 4,042652 | ||
| Столбцы | 3317,733 | 663,5467 | 129,6834 | 1,14E-26 | 2,408514 | ||
| Взаимодействие | 99,33333 | 19,86667 | 3,882736 | 0,004911 | 2,408514 | ||
| Внутри | 245,6 | 5,116667 | |||||
| Итого | 3665,933 |
Преобразуем итоговую таблицу (Таблица 3).
Табл. 3. Итоги двухфакторного дисперсионного анализа, проведенного с помощью "Анализа данных" (Преобразованная таблица).
| Источник вариации | SS | Степени свободы | Дисперсия (s2) | F | P-Значение | F критическое |
| Соленость (В) | 3,266667 | 3,267 | 0,638 | 0,428 | 4,043 | |
| Глубина (А) | 3317,733 | 663,547 | 129,683 | 0,000 | 2,409 | |
| Взаимодействие факторов (АВ) | 99,33333 | 19,867 | 3,883 | 0,005 | 2,409 | |
| Случайная | 245,6 | 5,117 | ||||
| Общая | 3665,933 |
Дальнейший анализ существенности влияния на исследуемый признак глубины и совместного влияния глубины и солености может быть продолжен в ходе оценки значимости силы влияния факторов на признак. Как и в случае однофакторного дисперсионного анализа можно оценить силу влияния значимого для исследуемого признака фактора (в нашем случае глубины и совместного влияния факторов). Расчет производится по аналогичной для однофакторного анализа схеме.
Пример. Оценим силу влияния глубины и совместного воздействия факторов на численность маком.
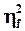 =
= 
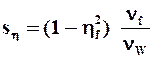
Результаты анализа представим в табличной форме (Табл. 4)
Нулевая гипотеза: влияние фактора соизмеримо с ошибкой оценки и потому вывод о достоверности отличия силы влияния от 0 не надежен.
На: сила влияния фактора больше 0.
Таблица 4. Оценка силы влияния фактора (глубины и совместного влияния солености и глубины) на численность моллюсков
| Источник вариации | SS | Степени свободы | Сила влияния фактора | Ошибка силы влияния | F | F критическое |
| Глубина (А) | 3317,733333 | 0,905 | 0,010 | 91,471 | 2,409 | |
| Взаимодействие факторов (АВ) | 99,33333333 | 0,027 | 0,101 | 0,267 | 2,409 | |
| Случайная | 245,6 | |||||
| Общая | 3665,933333 |
В результате мы отвергаем нулевую гипотезу в отношении силы влияния глубины на численность моллюсков и принимаем в отношении силы совместного влияния факторов.
В результате проведенных исследований оказалось, что на количественное распределение моллюсков достоверное влияние оказывает только глубина.
Date: 2015-09-05; view: 524; Нарушение авторских прав