
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры
|
|
1) В пространстве  геометрических векторов с обычным скалярным произведением неравенства Коши–Буняковского и Минковского имеют вид:
геометрических векторов с обычным скалярным произведением неравенства Коши–Буняковского и Минковского имеют вид:

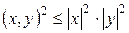 ,
, 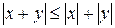 .
.
Первое неравенство в силу  означает, что
означает, что 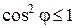 , второе − что длина стороны треугольника не превосходят суммы длин двух других сторон.
, второе − что длина стороны треугольника не превосходят суммы длин двух других сторон.
2) В  неравенства Коши–Буняковского и Минковского дают:
неравенства Коши–Буняковского и Минковского дают:
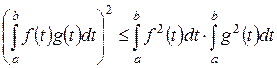
 .
.
3) В 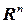 с обычным скалярным произведением и
с обычным скалярным произведением и 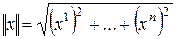 имеем
имеем
неравенство Коши–Буняковского
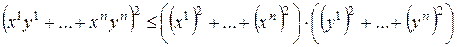 ;
;
неравенство Минковского
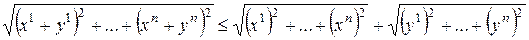 .
.
4) В 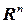 со скалярным произведением с положительно определённой симметрической матрицей
со скалярным произведением с положительно определённой симметрической матрицей 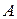 имеем
имеем
неравенство Коши–Буняковского
 ;
;
неравенство Минковского

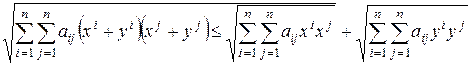 .
.
Замечание. Если векторное пространство 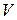 дано над полем
дано над полем  , то аналогично строится теория унитарных (или эрмитовых) пространств. В этом случае аксиомы 1) и 4) принимают соответственно вид:
, то аналогично строится теория унитарных (или эрмитовых) пространств. В этом случае аксиомы 1) и 4) принимают соответственно вид:
1)  ;
;
4)  и
и 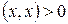 , если
, если 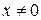 .
.
Отметим, что неравенство Коши–Буняковского в этом случае принимает вид:
 .
.
В 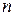 –мерном комплексном координатном пространстве C
–мерном комплексном координатном пространстве C  стандартное скалярное произведение векторов
стандартное скалярное произведение векторов  C
C  задается формулой
задается формулой
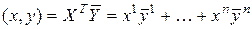 .
.
2°. Ортогональные и ортонормированные системы векторов.
Из неравенства Коши–Буняковского следует, что корректно можно ввести следующее
Определение 3. Для любых 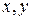 принадлежащих евклидовому пространству E определен угол
принадлежащих евклидовому пространству E определен угол 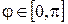 между ними:
между ними:  .
.
Определение 4. Элементы 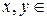 E
E 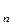 называются ортогональными, если их скалярное произведение равно нулю, то есть
называются ортогональными, если их скалярное произведение равно нулю, то есть 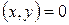 . Тогда
. Тогда 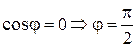 .
.
Очевидно, что если  ортогонален
ортогонален 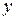 , то
, то 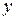 ортогонален
ортогонален 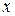
 .
.
Лемма 1. Нулевой вектор ортогонален любому вектору из E 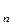 и является единственным вектором, обладающим этим свойством.
и является единственным вектором, обладающим этим свойством.
Доказательство самостоятельно.
Определение 5. Сумму 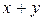 двух ортогональных векторов
двух ортогональных векторов 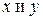 назовем гипотенузой треугольника, построенного на векторах
назовем гипотенузой треугольника, построенного на векторах 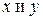 .
.
Лемма 2. Квадрат гипотенузы равен сумме квадратов катетов.
Доказательство: 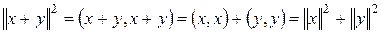 .■
.■
Обобщение. Если 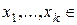 E
E 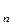 − взаимно ортогональны Þ
− взаимно ортогональны Þ
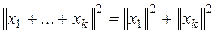 .
.
Определение 6. Система векторов евклидова пространства E 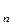 называется ортогональной, если она либо состоит из одного вектора, либо её векторы попарно ортогональны.
называется ортогональной, если она либо состоит из одного вектора, либо её векторы попарно ортогональны.
Теорема 3. Всякая ортогональная система ненулевых векторов евклидова пространства является линейно независимой.
Доказательство: Пусть 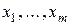 − ортогональная система векторов и пусть
− ортогональная система векторов и пусть
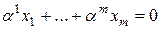
с некоторыми постоянными  . Умножая это равенство скалярно на
. Умножая это равенство скалярно на 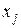 , получаем
, получаем
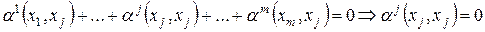 .
.
Т.к. 
 все
все 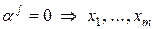 − линейно независимы. ■
− линейно независимы. ■
Определение 7. Ортогональная система, состоящая из векторов единичной длины, называется ортонормированной.
Определение 8. В 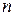 –мерном евклидовом пространстве E
–мерном евклидовом пространстве E 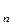 система
система 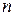 ортонормированных векторов образует ортонормированный базис.
ортонормированных векторов образует ортонормированный базис.
Теорема 4. Во всяком 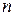 –мерном евклидовом пространстве E
–мерном евклидовом пространстве E 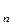 существует ортонормированный базис.
существует ортонормированный базис.
Доказательство. Т.к. пространство E 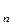 −
− 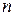 –мерное, то существуют
–мерное, то существуют 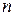 векторов
векторов 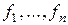 , которые линейно независимы. Покажем, что можно построить векторы
, которые линейно независимы. Покажем, что можно построить векторы 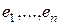 , получающиеся как линейные комбинации
, получающиеся как линейные комбинации  , которые образуют ортонормированный базис. Доказательство методом математической индукции:
, которые образуют ортонормированный базис. Доказательство методом математической индукции:
Если 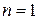 − очевидно, т.к.
− очевидно, т.к. 
Пусть удалось построить 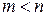 векторов
векторов 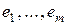 , которые попарно ортогональны, их нормы равны единице, и получены как линейные комбинации
, которые попарно ортогональны, их нормы равны единице, и получены как линейные комбинации  . Будем искать вектор
. Будем искать вектор  . Выберем
. Выберем  так, чтобы
так, чтобы 
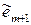 был ортогонален
был ортогонален 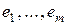 . Умножая
. Умножая 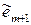 скалярно на
скалярно на  , в силу ортонормированности
, в силу ортонормированности 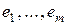 имеем:
имеем:
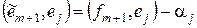 Þ //т.к.
Þ //т.к. 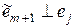 // Þ
// Þ  .
.
Очевидно, что полученный  , т.к. он является линейной комбинацией
, т.к. он является линейной комбинацией 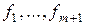 Þ
Þ 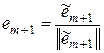 Þ система
Þ система 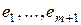 − ортонормированная и получена как линейная комбинация
− ортонормированная и получена как линейная комбинация 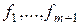 . ■
. ■
Замечание 1. В доказательстве теоремы 4 использовался следующий алгоритм ортогонализации системы векторов, известный как алгоритм Грамма–Шмидта:
пусть 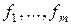 − линейно независимы. Тогда попарно ортогональные единичные вектора получаются по следующим формулам:
− линейно независимы. Тогда попарно ортогональные единичные вектора получаются по следующим формулам:
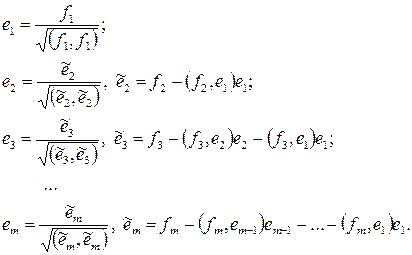
| (4) |
Замечание 2. В любом евклидовом пространстве можно построить много ортонормированных базисов. Примером ортонормированного базиса в  с обычным скалярным произведением могут служить вектора
с обычным скалярным произведением могут служить вектора

Рассмотрим произвольный ортонормированный базис 
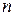 -мерного евклидова пространства E
-мерного евклидова пространства E 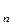 . Пусть
. Пусть 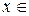 E
E 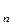 − произвольный вектор и
− произвольный вектор и
 .
.
Умножая обе части равенства скалярно на 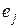 получим:
получим:
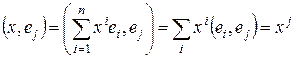 ,
,
т.е. координаты произвольного вектора относительно ортонормированного базиса равны скалярным произведениям этого вектора на соответствующие базисные векторы. Поскольку скалярное произведение 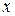 на вектор
на вектор 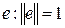 , естественно назвать проекцией
, естественно назвать проекцией 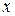 на
на  , то, следовательно, координаты произвольного
, то, следовательно, координаты произвольного 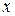 относительно ортонормированного базиса равны проекциям этого элемента на соответствующие базисные элементы.
относительно ортонормированного базиса равны проекциям этого элемента на соответствующие базисные элементы.
Таким образом, ортонормированный базис похож на ортонормированный базис в пространстве геометрических векторов.
3°. Выражение скалярного произведения через компоненты сомножителей. Матрица Грама.
Пусть в произвольном евклидовом пространстве E 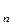 задан базис
задан базис  . Это позволяет
. Это позволяет 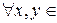 E
E 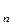 представить в виде
представить в виде 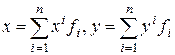 . Вычислим скалярное произведение
. Вычислим скалярное произведение 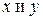 :
:
 .
.
Отсюда следует, что если базис 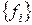 − ортонормированный, то есть
− ортонормированный, то есть  , то
, то
 .
.
Теорема 5. В ортонормированном базисе скалярное произведение любых двух векторов равно сумме произведений соответствующих координат этих векторов.
Если же базис {  } − произвольный, то произведения
} − произвольный, то произведения 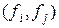 обозначим
обозначим  и введем в рассмотрение квадратную матрицу
и введем в рассмотрение квадратную матрицу
 =
=  =
= 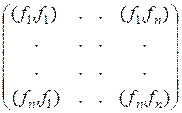 ,
,
называемую матрицей Грама базиса {  }. В силу коммутативности скалярного произведения
}. В силу коммутативности скалярного произведения 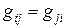 , т.е. матрица Грама симметрическая.
, т.е. матрица Грама симметрическая.
Обозначим  =
= 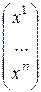 ,
, 
 . Тогда скалярное произведение
. Тогда скалярное произведение 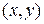 можно переписать в матричном виде:
можно переписать в матричном виде:
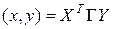 .
.
Если {  } − ортонормированный, то
} − ортонормированный, то  и
и 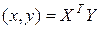 .
.
Рассмотрим два базиса {  } и {
} и {  }, связанные при помощи матрицы перехода
}, связанные при помощи матрицы перехода  : если
: если 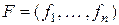 и
и 
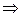
 , т.е.
, т.е. 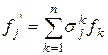 . Тогда для базиса {
. Тогда для базиса { 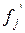 } матрица Грама имеет вид:
} матрица Грама имеет вид:
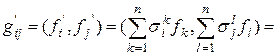   . .
| (5) |
Эта формула даёт связь между матрицами Грама для двух связанных между собой базисов. Равенство (5) в матричном виде имеет вид:
 , ,
| (6) |
что легко проверить прямыми вычислениями.
Рассмотрим последнюю формулу в частном случае, когда {  } – ортонормированный. Тогда
} – ортонормированный. Тогда  и формула (6) имеет вид:
и формула (6) имеет вид:
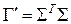 ,
,
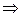 вычисляя определитель в силу теоремы об определителе произведения матриц, имеем:
вычисляя определитель в силу теоремы об определителе произведения матриц, имеем:
 .
.
Так как { 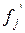 } – произвольный базис
} – произвольный базис 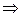 // т.к. det
// т.к. det 
 0 //
0 // 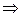
Теорема 6. Определитель матрицы Грама любого базиса положителен.
Эта теорема может быть усилена.
Теорема 7. Пусть  ,…,
,…, 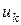 − произвольные (не обязательно линейно независимые) вектора в евклидовом пространстве. Тогда определитель матрицы
− произвольные (не обязательно линейно независимые) вектора в евклидовом пространстве. Тогда определитель матрицы
 ,
,
составленной из попарных скалярных произведений, положителен, если вектора линейно независимы, и равен нулю, если они линейно зависимы.
Доказательство. Первое утверждение теоремы следует из теоремы 6, т.к. если  ,…,
,…, 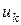 − линейно независимы, то они образуют базис в своей линейной оболочке.
− линейно независимы, то они образуют базис в своей линейной оболочке.
Докажем второе утверждение. Если векторы  – линейно зависимы, то выполнено равенство
– линейно зависимы, то выполнено равенство  , где хотя бы одно
, где хотя бы одно 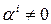 . Умножая это равенство скалярно на каждый из векторов
. Умножая это равенство скалярно на каждый из векторов  получим систему уравнений
получим систему уравнений
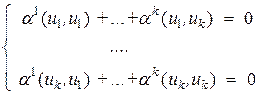 ,
,
которой удовлетворяет ненулевое решение 
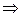 определитель матрицы этой системы равен нулю.■
определитель матрицы этой системы равен нулю.■
Замечание. Доказанная теорема обобщает неравенство Коши–Буняковского, которое имеет место при 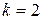 .
.
4˚. Ортогональное дополнение к линейному подпространству.
Определение 9. Два множества 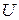 и
и 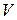 векторов евклидова пространства E
векторов евклидова пространства E 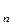 называются ортогональными, если каждый вектор первого множества ортогонален к каждому вектору второго.
называются ортогональными, если каждый вектор первого множества ортогонален к каждому вектору второго.
В частности, будем говорить, что вектор 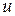 ортогонален к множеству
ортогонален к множеству 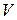 , если
, если 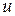 ортогонален каждому
ортогонален каждому 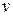

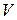 .
.
Ортогональность 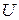 и
и 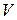 обозначается
обозначается 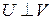 .
.
Лемма 3. Если два множества 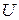 и
и 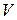 ортогональны, то их пересечение либо пусто, либо состоит только из нулевого вектора.
ортогональны, то их пересечение либо пусто, либо состоит только из нулевого вектора.
Доказательство. На самом деле, если 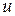
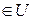 и
и 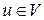
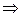
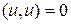
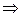
 . ■
. ■
Следствие. Сумма ортогональных подпространств всегда является прямой суммой.
Доказательство. Это следует из того, что их пересечение в силу леммы 3 состоит только из нулевого вектора 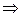 сумма прямая. ■
сумма прямая. ■
Пусть 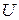 – подпространство евклидового пространства.
– подпространство евклидового пространства.
Определение 10. Ортогональным дополнением подпространства 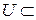 E
E 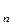 называется множество всех векторов, перпендикулярных каждому вектору из
называется множество всех векторов, перпендикулярных каждому вектору из 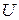 .
.
Ортогональное дополнение к 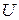 обозначается
обозначается 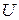
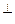 .
.
Очевидно, что 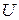 – линейное подпространство; на самом деле, если
– линейное подпространство; на самом деле, если 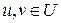
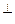 , а
, а  , то (
, то ( u+
u+ 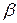 v,w) =
v,w) =  (u,w)+
(u,w)+ 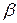 (v,w) = О
(v,w) = О 
 u +
u + 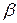 v
v  U
U  ,что и требовалось доказать.
,что и требовалось доказать.
Теорема 8. Евклидово пространство E 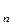 есть прямая сумма любого своего подпространства U и его ортогонального дополнения U
есть прямая сумма любого своего подпространства U и его ортогонального дополнения U 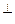 .
.
Доказательство. Пусть dim U=k и пусть e  ,…, e
,…, e  − ортонормированный базис в U. В силу известной теоремы эти вектора можно дополнить до базиса
− ортонормированный базис в U. В силу известной теоремы эти вектора можно дополнить до базиса  во всём пространстве
во всём пространстве 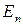 . Применяя к ним процесс ортогонализации Грама-Шмидта, получим ортонормированный базис e
. Применяя к ним процесс ортогонализации Грама-Шмидта, получим ортонормированный базис e  ,…, e
,…, e  евклидова пространства
евклидова пространства 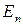 .
.
Любой элемент х  E
E 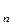 может быть разложен по этому базису:
может быть разложен по этому базису:
x = x  e
e  +…+ x
+…+ x 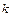 e
e  + x
+ x 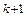 e
e 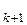 +… +x
+… +x  e
e  ,
,
т.е. х=x  +x
+x 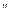 , где x
, где x  = x
= x  e
e  +…+ x
+…+ x 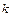 e
e 
 U, а x
U, а x 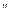 = x
= x 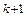 e
e 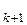 +… +x
+… +x  e
e 
 U
U 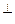 ,
,
в силу ортонормированности базиса. Следовательно, в силу следствия к лемме 3, сумма U и U 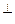 – прямая сумма. ■
– прямая сумма. ■
Следствие 1. (U 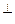 )
) 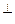 = U.
= U.
Следствие 2. 
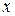
 E
E 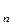 может быть единственным образом представлен в виде х= x
может быть единственным образом представлен в виде х= x  +x
+x 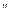 , где x
, где x 
 U, x
U, x 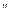
 U
U 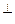 . При этом x
. При этом x  называется ортогональной проекцией вектора
называется ортогональной проекцией вектора 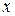 на подпространство U, а x
на подпространство U, а x 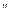 − ортогональной составляющей
− ортогональной составляющей 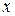 относительно U.
относительно U.
Задача. В E 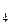 подпространство U натянуто на векторы
подпространство U натянуто на векторы 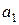 =(1,0,1,1), и
=(1,0,1,1), и 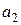 =(0,1,1,–1). Найти ортогональную проекцию и ортогональную составляющую вектора
=(0,1,1,–1). Найти ортогональную проекцию и ортогональную составляющую вектора 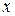 =(1,2,0,1) на подпространство U.
=(1,2,0,1) на подпространство U.
Решение. 1 способ. Вектора 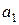 и
и 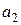 − ортогональны. Нормируя их, получаем:
− ортогональны. Нормируя их, получаем:
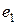 =
= 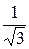 (1;0;1;1);
(1;0;1;1); 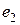 =
= 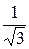 (0;1;1;–1).
(0;1;1;–1).  Если
Если 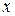 = x
= x 
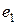 +x
+x 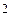
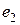 + x
+ x 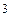
 +x
+x 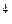
 , то
, то
x  = (
= (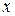 ,
, 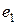 ) =
) = 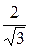 ; x
; x 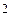 = (
= (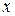 ,
, 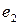 ) =
) = 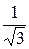
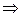 Если x = x
Если x = x  +x
+x 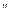
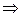
x  = x
= x 
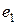 +x
+x 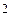
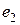 = (
= (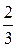 ;
;  ;1;
;1;  ).
). 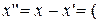
 ;
; 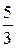 ;–1;
;–1; 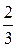 ).
).
2 способ. Применим процесс ортогонализации к базису в 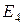 :
: 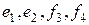 .
.
Выберем 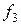 = (0;0;1;0),
= (0;0;1;0),  = (0;0;0;1)
= (0;0;0;1) 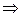 ортогонализация даёт:
ортогонализация даёт:
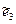 =
= 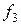 – (
– (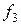 , e
, e  ) e
) e  – (
– (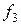 , e
, e 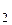 ) e
) e 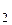 = (–
= (–  ;–
;–  ;
;  ;0)
;0) 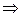
 = (–
= (– 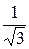 ;–
;– 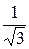 ;
; 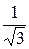 ;0). Аналогично,
;0). Аналогично,  = (–
= (– 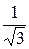 ;
; 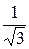 ;0;
;0; 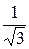 ).
).
 Решим систему:
Решим систему: 
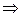
x  =
= 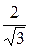 , x
, x 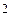 =
= 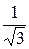 , x
, x 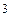 =-
=- 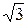 , x
, x 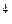 =
= 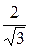
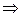 x
x  =x
=x 
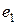 +x
+x 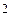
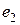 ; x
; x  =x
=x 
 +x
+x 
 .
.
Date: 2015-09-03; view: 548; Нарушение авторских прав