Аналитическое сглаживание временного ряда. Уравнение тренда

Кривые роста, описывающие закономерности развития явлений во времени – это результат аналитического выравнивания динамических рядов. Выравнивание ряда с помощью тех или иных функций в большинстве случаев оказывается удобным средством описания эмпирических данных. Это средство при соблюдении ряда условий можно применить и для прогнозирования. Процесс выравнивания состоит из следующих основных этапов:

- выбора типа кривой, форма которой соответствует характеру изменения динамического ряда;

- определения численных значений (оценка) параметров кривой;

- апостериорного контроля качества выбранного тренда.

В современных ППП все перечисленные этапы реализуются одновременно, как правило, в рамках одной процедуры.

Аналитическое сглаживание с использованием той или иной функции позволяет получить выровненные, или, как их иногда не вполне правомерно называют, теоретические значения уровней динамического ряда, т. е. уровни, которые наблюдались бы, если бы динамика явления полностью совпадала с кривой. Эта же функция с некоторой корректировкой или без нее, применяется в качестве модели для экстраполяции (прогноза).

Вопрос о выборе типа кривой является основным при выравнивании ряда. При всех прочих равных условиях ошибка в решении этого вопроса оказывается более значимой по своим последствиям (особенно для прогнозирования), чем ошибка, связанная со статистическим оцениванием параметров.

Поскольку форма тренда объективно существует, то при выявлении ее следует исходить из материальной природы изучаемого явления, исследуя внутренние причины его развития, а также внешние условия и факторы на него влияющие. Только после глубокого содержательного анализа можно переходить к использованию специальных приемов, разработанных статистикой.

Весьма распространенным приемом выявления формы тренда является графическое изображение временного ряда. Но при этом велико влияние субъективного фактора, даже при отображении выровненных уровней.

Наиболее надежные методы выбора уравнения тренда основаны на свойствах различных кривых, применяемых при аналитическом выравнивании. Такой подход позволяет увязать тип тренда с теми или иными качественными свойствами развития явления. Нам представляется, что в большинстве случаев практически приемлемым является метод, который основывается на сравнении характеристик изменения приростов исследуемого динамического ряда с соответствующими характеристиками кривых роста. Для выравнивания выбирается та кривая, закон изменения прироста которой наиболее близок к закономерности изменения фактических данных.

При выборе формы кривой надо иметь в виду еще одно обстоятельство. Рост сложности кривой в целом ряде случаев может действительно увеличить точность описания тренда в прошлом, однако в связи с тем, что более сложные кривые содержат большее число параметров и более высокие степени независимой переменной, их доверительные интервалы будут, в общем, существенно шире, чем у более простых кривых при одном и том же периоде упреждения.

В настоящее время, когда использование специальных программ без особых усилий позволяет одновременно строить несколько видов уравнений, широко эксплуатируются формальные статистические критерии для определения лучшего уравнения тренда.

Из сказанного выше, по-видимому, можно сделать вывод о том, что выбор формы кривой для выравнивания представляет собой задачу, которая не решается однозначно, а сводится к получению ряда альтернатив. Окончательный выбор не может лежать в области формального анализа, тем более, если предполагается с помощью выравнивания не только статистически описать закономерность поведения уровня в прошлом, но и экстраполировать найденную закономерность в будущее. Вместе с тем различные статистические приемы обработки данных наблюдения могут принести существенную пользу, по крайней мере, с их помощью можно отвергнуть заведомо непригодные варианты и тем самым существенно ограничить поле выбора.

Рассмотрим наиболее используемые типы уравнений тренда:

1. Линейная форма тренда:

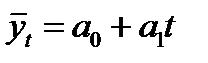, (3.5)

где 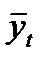– уровень ряда, полученный в результате выравнивания по прямой; – начальный уровень тренда; 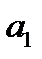– средний абсолютный прирост, константа тренда.

Для линейной формы тренда характерно равенство так называемых первых разностей (абсолютных приростов) и нулевые вторые разности, т. е. ускорения.

2. Параболическая (полином 2-ой степени) форма тренда:

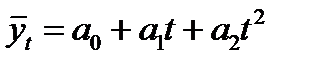(3.6)

Для данного типа кривой постоянными являются вторые разности (ускорение), а нулевыми – третьи разности.

Параболическая форма тренда соответствует ускоренному или замедленному изменению уровней ряда с постоянным ускорением. Есл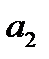и < 0 и 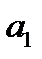> 0, то квадратическая парабола имеет максимум, есл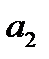и > 0 и 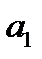< 0 – минимум. Для отыскания экстремума первую производную параболы по t приравнивают 0 и решают уравнение относительно t.

3. Логарифмическая форма тренда:

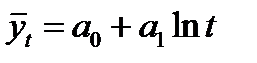, (3.7)

где 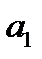– константа тренда.

Логарифмическим трендом может быть описана тенденция, проявляющаяся в замедлении роста уровней ряда динамики при отсутствии предельно возможного значения. При достаточно большом t логарифмическая кривая становится мало отличимой от прямой линии.

4. Мультипликативная (степенная) форма тренда:

(3.8)

5. Полином 3-ей степени:

(3.9)

Естественно, кривых, описывающих основные тенденции, гораздо больше. Однако формат учебного пособия не позволяет описать все их многообразие. Показанные далее приемы построения моделей позволят пользователю самостоятельно использовать другие функции, в частности обратные.

Для решения поставленной задачи по аналитическому сглаживанию динамических рядов в системе STATISTICA нам потребуется создать дополнительную переменную на листе с исходными данными переменной «ВГ2001-2010», который следует сделать активным.

Нам предстоит построить уравнение тренда, которое по существу является уравнением регрессии, в котором в качестве фактора выступает «время». Создаем переменную «Т», содержащую интервалы времени, 10 годам (с 2001 по 2010). Переменная «Т» будет состоять из натуральных чисел от 1 до 10, соответствующих указанным годам.

В итоге получается следующий рабочий лист (рис. 3.6)

Рис. 3.6. Рабочий лист с созданной переменной времени

Далее рассмотрим процедуру, позволяющую строить регрессионные модели как линейного, так и нелинейного типа. Для этого выбираем: Statistics/Advanced Linear/Nonlinear Models/Nonlinear Estimation (рис. 3.7). В появившемся окне (рис. 3.8) выбираем функцию User-specified Regression, Least Squares (построение моделей регрессии пользователем вручную, параметры уравнения находятся по методу наименьших квадратов (МНК)).

В следующем диалоговом окне (рис. 3.9) нажимаем на кнопку Function to be estimated, чтобы попасть на экран для задания модели вручную (рис. 3.10).

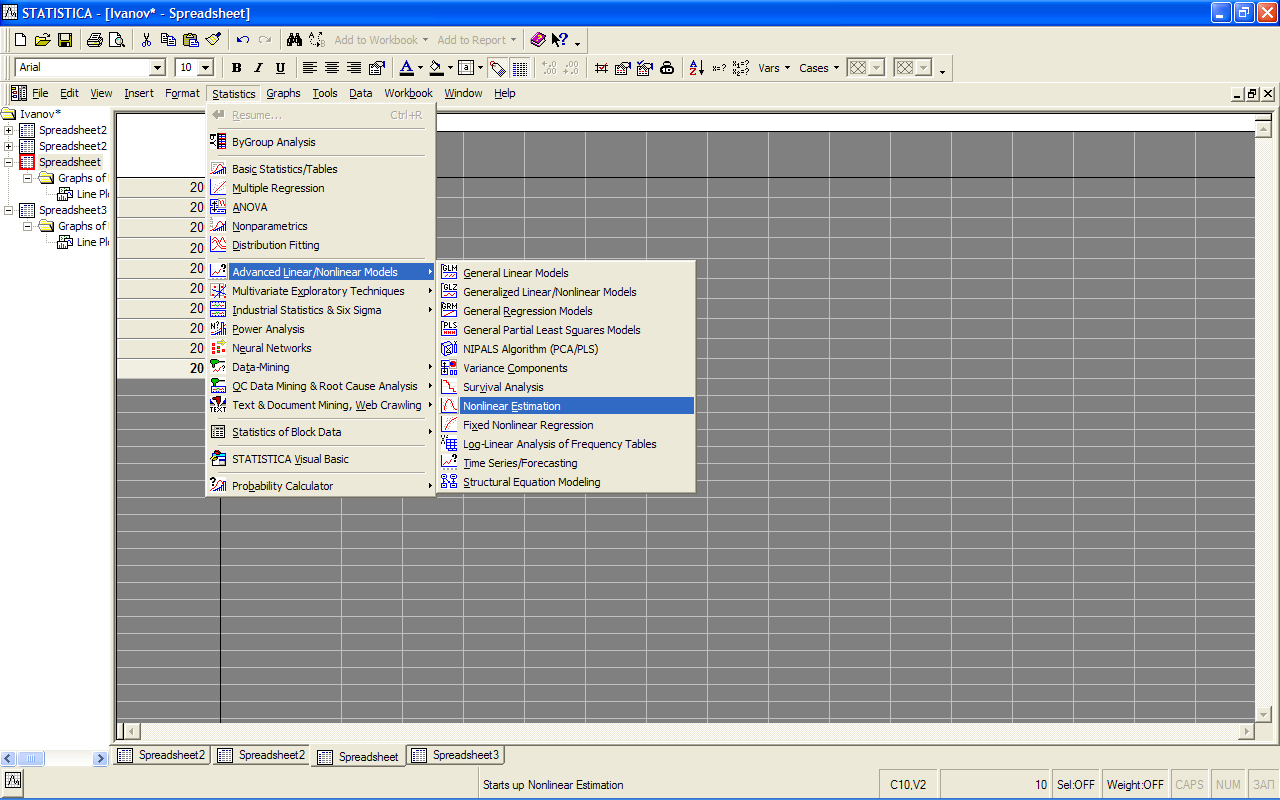
Рис. 3.7. Запуск процедуры Statistics/Advanced Linear/

Nonlinear Models/Nonlinear Estimation

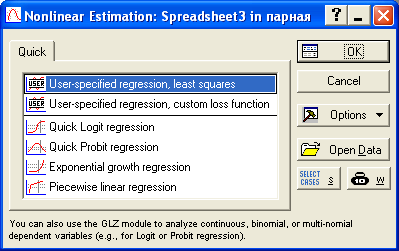
Рис. 3.8. Окно процедуры Nonlinear Estimation

Рис. 3.9ю Окно процедуры User-Specified Regression, Least Squares

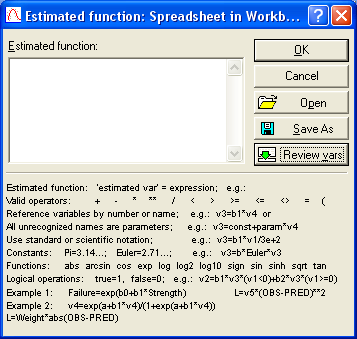
Рис. 3.10. Окно для реализации процедуры

задания уравнения тренда вручную

В верхней части экрана находится поле для ввода функции, в нижней части располагаются примеры ввода функций для различных ситуаций.

Прежде чем сформировать интересующие нас модели, необходимо пояснить некоторые условные обозначения. Переменные уравнений задаются в формате «v №», где «v» обозначает переменную (от англ. «variable»), а «№» – номер столбца, в котором она расположена в таблице на рабочем листе с исходными данными. Если переменных очень много, то справа находится кнопка Review vars, позволяющая выбирать их из списка по названиям и просматривать их параметры с помощью кнопки Zoom (рис. 3.11).

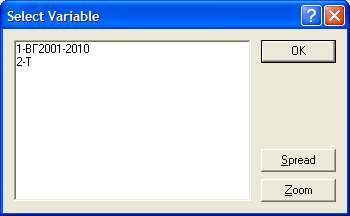
Рис. 3.11. Окно выбора переменной с помощью кнопки Review vars

Параметры уравнений обозначаются любыми латинскими буквами, не обозначающими какое-либо математическое действие. Для упрощения работы предлагается обозначать параметры уравнения так, как в описании уравнений тренда – латинской буквой «а», последовательно присваивая им порядковые номера. Знаки математических действий (вычитания, сложения, умножения и пр.) задаются в обычном для Windows -приложений формате. Пробелы между элементами уравнения не требуются.

Итак, рассмотрим первую модель тренда – линейную, .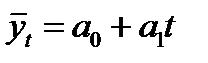

Следовательно, после набора она будет выглядеть следующим образом:

,

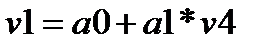где v 1 – это столбец на листе с исходными данными, в котором находятся значения исходного динамического ряда; а 0 и а 1 – параметры уравнения; v 2 – столбец на листе с исходными данными, в котором находятся значения интервалов времени (переменная Т) (рис. 3.12).

После этого дважды нажимаем кнопку ОК.

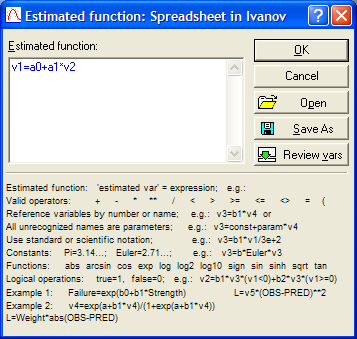
Рис. 3.12. Окно процедуры задания уравнения линейного тренда

Рис. 3.13. Закладка Quick процедуры оценки уравнения тренда.

В появившемся окне (рис. 3.13) можно выбрать метод оценки параметров уравнения регрессии (Estimation method), если это необходимо. В нашем случае нужно перейти к закладке Advanced и нажать на кнопку Start values (рис. 3.14). В этом диалоге задаются стартовые значения параметров уравнения для их нахождения по МНК, т.е. их минимальные значения. Изначально они заданы как 0,1 для всех параметров. В нашем случае можно оставить эти значения в том же виде, но если значения в наших исходных данных меньше единицы, то необходимо задать их в виде 0,001 для всех параметров уравнения тренда (рис. 3.15). Далее нажимаем кнопку ОК.

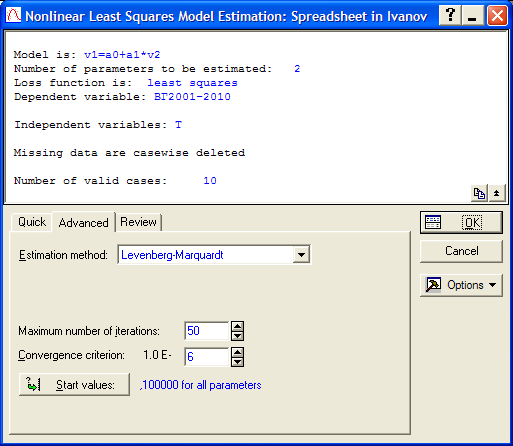
Рис. 3.14. Закладка Advanced процедуры оценки уравнения тренда

Рис. 3.15. Окно задания стартовыхзначений параметров уравнения тренда

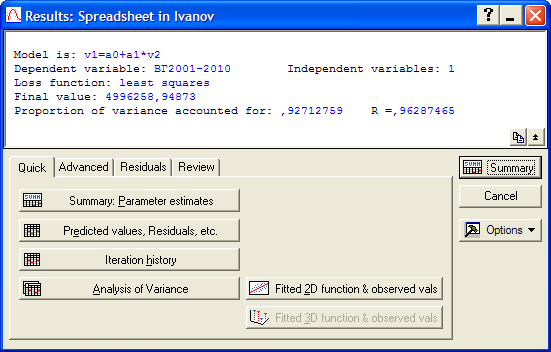
Рис. 3.16. Закладка Quick окна результатов регрессионного анализа

На закладке Quick (рис.3.16) очень важным является значение строчки Proportion of variance accounted for, которое соответствует коэффициенту детерминации; это значение лучше записать отдельно, так как в дальнейшем оно выводиться не будет, и пользователю придется рассчитывать коэффициент вручную, при этом достаточно трех знаков после запятой[3]. Далее нажимаем кнопку Summary: Parameter estimates для получения данных о параметрах линейного уравнения тренда (рис. 3.17).

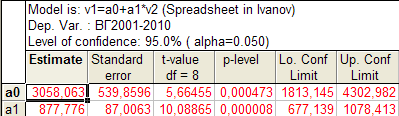
Рис. 3.17. Результаты расчета параметров линейной модели тренда

Столбец Estimate – числовые значения параметров уравнения; Standard еrror – стандартная ошибка параметра; t-value – расчетное значение t -критерия; df – число степеней свободы (n -2); p-level – расчетный уровень значимости; Lo. Conf. Limit и Up. Conf. Limit – соответственно нижняя и верхняя граница доверительных интервалов для параметров уравнения с установленной вероятностью (указана как Level of Confidence в верхнем поле таблицы).

Соответственно уравнение линейно модели тренда имеет вид .

После этого возвращаемся к анализу и нажимаем на кнопку Analysis of Variance (дисперсионный анализ) на той же закладке Quick (см. рис. 3.16).

Опишем содержание появившейся таблицы (рис. 3.18).

Рис. 3.18. Результаты дисперсионного анализа линейной модели тренда

В верхней заголовочной строке таблицы выдаются пять оценок:

Sum of Squares – сумма квадратов отклонений; df – число степеней свободы; Mean Squares – средний квадрат; F-value – критерий Фишера; p-value – расчетный уровень значимости F -критерия.

В левом столбце указывается источник вариации:

Regression – вариация, объясненная уравнением тренда; Residual – вариация остатков – отклонений фактических значений от выровненных (полученных по уравнению тренда); Total – общая вариация переменной.

На пересечении столбцов и строк получаем однозначно определенные показатели, расчетные формулы для которых представлены в табл. 3.2,

Таблица 3.2

Расчет показателей вариации трендовых моделей

Source	df	Sum of Squares	Mean squares	F-value
Regression	m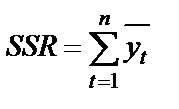
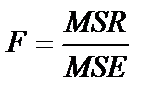
Residual	n-m
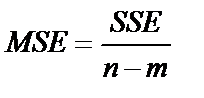
Total	n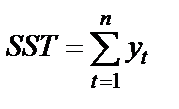
Corrected Total	n-1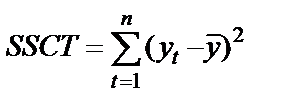
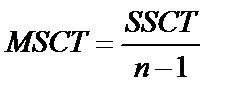
Regresion vs. Corrected Total	m	SSR	MSR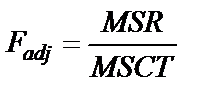

где 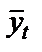– выровненные значения уровней динамического ряда; – фактические значения уровней динамического ряда; – среднее значение уровней динамического ряда.

SSR (Regression Sum of Squares) – сумма квадратов прогнозных значений; SSE (Residual Sum of Squares) – сумма квадратов отклонений теоретических и фактических значений 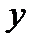(для расчета остаточной, необъясненной дисперсии); SST (TotalSum of Squares) – сумма первой и второй строчки (сумма квадратов фактических значений); SSCT (Corrected TotalSum of Squares) – сумма квадратов отклонений фактических значений 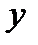от средней величины (для расчета общей дисперсии); Regression vs. Corrected Total Sum of Squares – повторение первой строчки; MSR (Regression Mean Squares) – объясненная дисперсия; MSE (Residual Mean Squares) – остаточная, необъясненная дисперсия; MSCT (Mean Squares Corrected Total) – скорректированная общая дисперсия; Regression vs. Corrected Total Mean Squares – повторение первой строчки; Regression F-value – расчетное значение F -критерия; Regression vs. Corrected Total F-value – скорректированное расчетное значение F -критерия; n – число уровней ряда; m – число параметров уравнения тренда.

Далее опять же на закладке Quick (см. рис. 3.16) нажимаем кнопку Predicted values, Residuals, etc. После ее нажатия система строит таблицу, состоящую из трех столбцов (рис. 3.19).

Observed – наблюдаемые значения (то есть уровни исходного динамического ряда);

Predicted – прогнозные значения (полученные по уравнению тренда для данных моментов времени);

Residuals – остатки (разница между фактическими и прогнозными значениями).

Рис. 3.19. Таблица наблюдаемых, прогнозных значений и остатков

для линейной модели тренда

Далее целесообразно построить графическое изображение, на котором линия линейного тренда будет наложена на исходный динамический ряд – это позволит визуально оценить степень соответствия.

Для этого на рабочем листе (см. рис. 3.19) выделяем столбцы Observed и Predicted, щелкаем по ним правой кнопкой мыши и выбираем функции Graphs of Block Data/ Line Plot: Entire Columns. Построенному графику лучше всего присвоить название и подписать легенду, с тем, чтобы далее легко его идентифицировать (рис. 3.20).

ВНИМАНИЕ!!! Получившиеся графики и таблицы целесообразно переименовывать в дерев рабочей книги из-за их большого количества и во избежание путаницы.

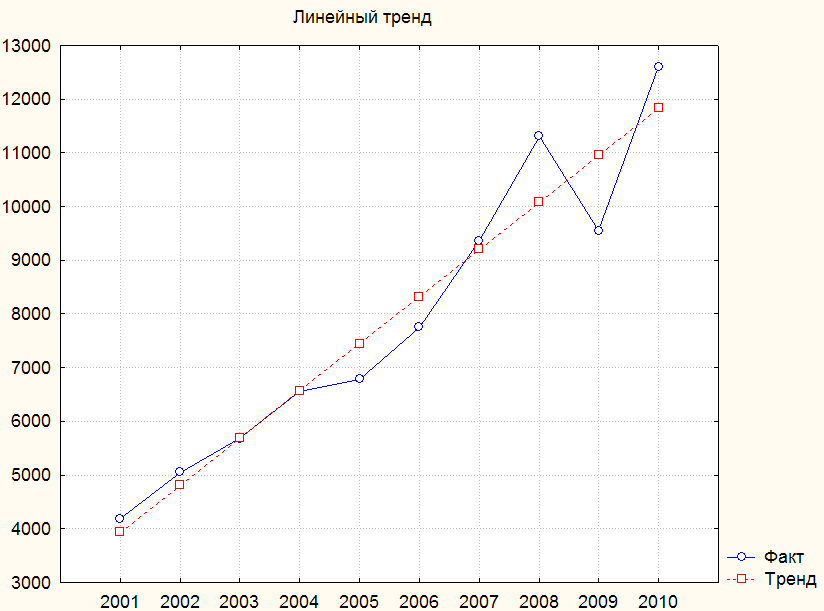
Рис. 3.20. Исходный динамический ряд и линейный тренд

Параметры уравнения тренда в STATISTICA, как и в большинстве других программ, рассчитываются по методу наименьших квадратов (МНК).

Метод позволяет получить значения параметров, при которых обеспечивается минимизация суммы квадратов отклонений фактических уровней от сглаженных, т. е. полученных в результате аналитического выравнивания.

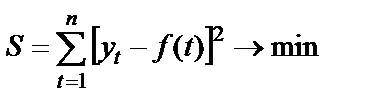(3.10)

Математический аппарат метода наименьших квадратов описан в большинстве работ по математической статистике, поэтому нет необходимости подробно на нем останавливаться.

В практике исследования социально-экономических явлений исключительно редко встречаются динамические ряды, характеристики которых полностью соответствуют признакам эталонных математических функций. Это обусловлено значительным числом факторов разного характера, влияющих на уровни ряда и тенденцию их изменения.

Итак, мы получили все необходимые результаты расчета параметров тренда, выраженного линейной моделью, а также построили график данного ряда, совмещенный с линией тренда.

На практике чаще всего строят целый ряд функций, описывающих тренд, а затем выбирают лучшую на основе того или иного формального критерия. В курсовом проекте предлагается построить пять трендовых моделей, функции которых представлены выше. В качестве примера приведем варианты построения параболической и логарифмической моделей на этапе ввода расчетной формулы в систему, получения уравнения тренда и с итоговым графиком (рис. 3.21 – 3.26). Отметим, что для попадания в меню ввода формулы достаточно нажать на кнопку Cancel текущего анализа (см. рис. 3.16).

Рис. 3.21. Окно процедуры задания уравнения параболической модели тренда

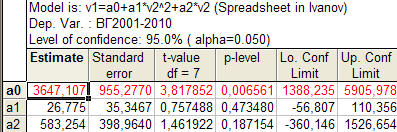
Рис. 3.22. Результаты расчета параметров параболической модели тренда

Рис. 3.23. Исходный динамический ряд и параболическая модель тренда

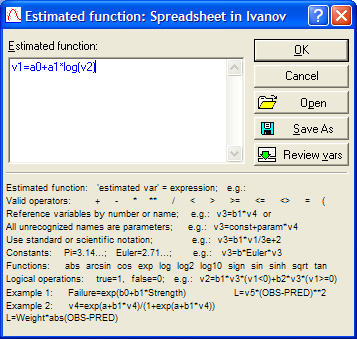
Рис. 3.24. Окно процедуры задания уравнения логарифмической модели тренда

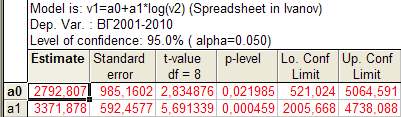
Рис. 3.25. Результаты расчета параметров логарифмической модели тренда

Рис. 3.26. Исходный динамический ряд и логарифмическая модель тренда

Date: 2015-09-03; view: 988; Нарушение авторских прав