Главная
Случайная страница
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
|
Теорема о скоростях точек плоской фигуры
Для любого момента времени r B = r A + r AB. Дифференцируя по времени r B с учетом | rA B | = const, получим v B = v A + v BA где v BA = d r AB/dt = w ´ r AB – вращательная скорость точки В относительно полюса А. Скорость некоторой точки В фигуры при плоском ее движении равна векторной сумме скорости полюса А и скорости этой точки в ее вращении вокруг полюса.
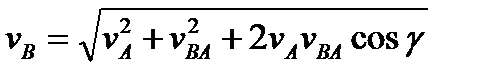 По модулю vBA = w× AB, т.к. вектор w ^пл.Оху, v BA ^ r AB. Таким образом v B = v A + w ´ r AB (2а) По модулю vBA = w× AB, т.к. вектор w ^пл.Оху, v BA ^ r AB. Таким образом v B = v A + w ´ r AB (2а)
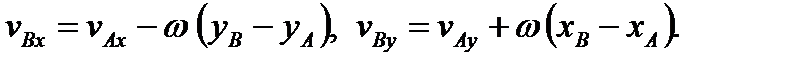 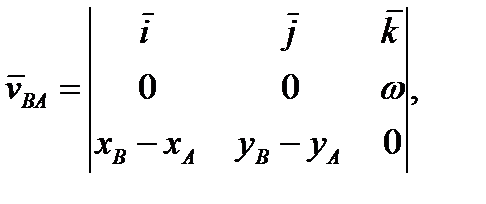 При известным угле g = Р v A, v BA Скорость vB можно также подсчитать, проецируя (2а) на оси координат: При известным угле g = Р v A, v BA Скорость vB можно также подсчитать, проецируя (2а) на оси координат:
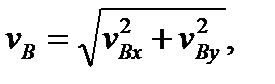
cos(vB, i) = vBx / vB.
15. Следствие 1. Проекции скоростей точек фигуры при плоском ее движении на линию, проходящую через эти точки, алгебраически равны.
Построим в точке В треугольник скоростей, рис.5. Проецируя (1) на ось х, проходящую через точки А и В, и учитывая, что v BA ^ AB, получим vA cosa = vB cosb.
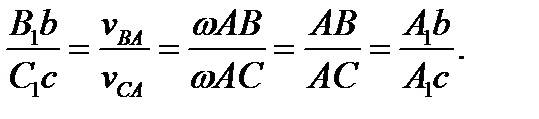 16. Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка. То есть АС/СВ = А1С1/С1В1, рис.6. Построим в точках В и С треугольники скоростей согласно (2). Фигура AA1 cbBCA – параллелограм, как построенная на векторах v A. Отсюда следует, что AC = A1c и BC = bc. Треугольники A1C1c и A1B1b подобны, так как 16. Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка. То есть АС/СВ = А1С1/С1В1, рис.6. Построим в точках В и С треугольники скоростей согласно (2). Фигура AA1 cbBCA – параллелограм, как построенная на векторах v A. Отсюда следует, что AC = A1c и BC = bc. Треугольники A1C1c и A1B1b подобны, так как
Следовательно, точки A1, B1 и C1 лежат на одной прямой.
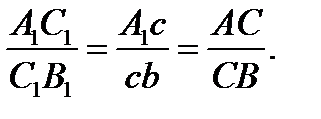 Из подобия треугольников следует Из подобия треугольников следует
17. Мгновенный центр скоростей (м.ц.с.) М.ц.с. – это точка плоской фигуры, скорость которой в данное мгновение равна нулю. Обозначим м.ц.с. как Р Доказательство существования м.ц.с. Пусть фигура, рис.7, совершает плоское движение. Скорость полюса А – vA, угловая скорость вращения вокруг полюса -w. Запишем для м.ц.с. теорему (1): v P = v A + v PA = 0, откуда при v P = 0 v A = - v PA, (5)
Отсюда следует правило нахождения м.ц.с.: Полупрямую, выходящую из точки А в направлении вектора v A следует повернуть на угол j = 900 в направлении вращения и на ней отложить отрезок АР = vA /w.
18. Расчет скоростей точек фигуры посредством м.ц.с
h AQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4 /SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQAl XyC11wMAANMJAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAA IQBbN46/4gAAAAkBAAAPAAAAAAAAAAAAAAAAADEGAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQA BADzAAAAQAcAAAAA " path="m-1,nfc11929,,21600,9670,21600,21600em-1,nsc11929,,21600,9670,21600,21600l,21600,-1,xe" filled="f" fillcolor="#4f81bd [3204]" strokecolor="black [3213]" strokeweight="2.25pt"> Запишем теорему (2) для точек A, B, C, D, приняв за полюс м.ц.с. Р:
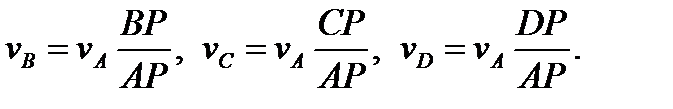
v A = v P + v AP = v AP, так как v P = 0. Аналогично v B = v BP, v C = v CP, v D = v DP. По модулю vA = vAP = wЧАР, vB = vBP = wЧBР, vC = vCP = wЧCР vD = vDP = wЧDР. Пусть известна скорость v A. Тогда w = vA/AP и скорости vB, vС, vD находятся по приведенным формулам. Подставляя w в формулы скоростей, получим
(6) Скорости точек относятся между собой также, как расстояния от этих точек до мгновенного центра скоростей
19. Способы определения м.ц.с. Даны vA, w. Далее см. п.4.1.
2) Известны vA точки А и направление движения точки В. М.ц.с. находится на пересечении перпендикуляров, проведенных через точки А и В к скорости vA и направлению движения точки В, рис.9. 3) При vA || vB и совпадении перпендикуляров АР и ВР м.ц.с. Р находится на основе формул (6), как показано на рис.10а и б. На рис. 10в и 11 показаны случаи, когда перпендикуляры к скоростям точек А и В параллельны между собой. М.ц.с. лежит в бесконечности, w = 0. Это случай мгновенно-поступательного движения. 4) В ряде случаев м.ц.с. можно установить визуально. Так, при качении колеса без проскальзывания м.ц.с. находится в точке соприкосновения колеса с поверхностью качения, рис.12.
Понятие о центроидах.
Совокупность м.ц.с. на подвижной фигуре образует линию I, которую называют подвижной центроидой. В каждый момент времени м.ц.с. совпадает с точкой, принадлежащей неподвижной системе координат, которую называют мгновенным центром вращения фигуры. Совокупность м.ц.в. в неподвижной системе координат образует неподвижную центроиду II. Движение плоской фигуры можно рассматривать как качение подвижной центроиды по неподвижной
20. Теорема. Ускорение точки при плоском движении фигуры равно векторной сумме ускорения полюса и ускорения точки в ее вращательном движении вокруг полюса.
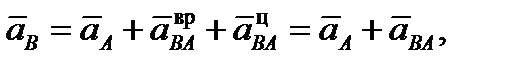 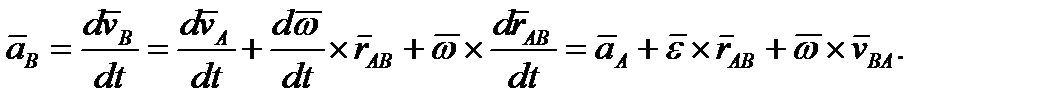 Запишем теорему о скорости некоторой точки фигуры В, v B = v A + w ´ r AB, где vA – скорость полюса А, и продифференцируем ее по времени Запишем теорему о скорости некоторой точки фигуры В, v B = v A + w ´ r AB, где vA – скорость полюса А, и продифференцируем ее по времени
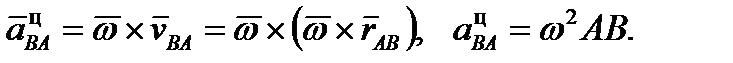 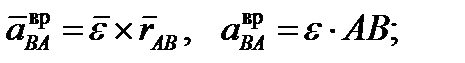 или (1) где или (1) где
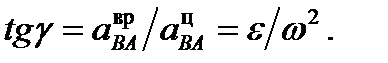 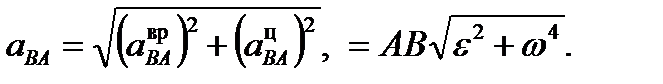 Модуль вращательного ускорения точки В вокруг полюса А (2) Угол g найдется из формулы Вращательное ускорение а ВАвр ^ АВ, центростремительное а ВАцнаправлено от точки В к полюсу А, рис. 1. Модуль вращательного ускорения точки В вокруг полюса А (2) Угол g найдется из формулы Вращательное ускорение а ВАвр ^ АВ, центростремительное а ВАцнаправлено от точки В к полюсу А, рис. 1.
21 Теорема о скорости точки при сложном ее движении
При сложном движении точки ее абсолютная скорость равна векторной сумме переносной и относительной скоростей.
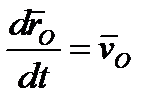 Для любого момента времени имеем, рис.3, r = r O + r (5) Дифференцируя (5) по времени, получим Для любого момента времени имеем, рис.3, r = r O + r (5) Дифференцируя (5) по времени, получим
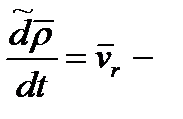 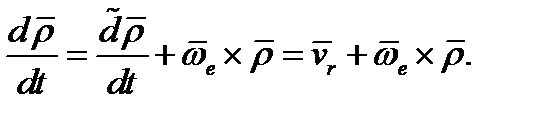 Производная - скорость начала подвижной системы координат О. Производная - скорость начала подвижной системы координат О.
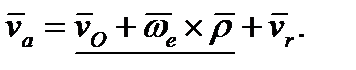 Производная согласно формуле Бура Здесь Производная согласно формуле Бура Здесь
относительная скорость точки. Следовательно, (6)
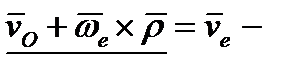 Подчеркнутые слагаемые представляют собой скорость той точки подвижной системы Подчеркнутые слагаемые представляют собой скорость той точки подвижной системы
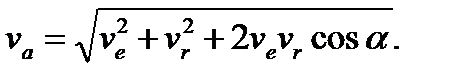 координат, с которой совпадает точка М. Следовательно, переносная скорость точки М. Окончательно координат, с которой совпадает точка М. Следовательно, переносная скорость точки М. Окончательно 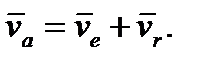 (7) Модуль (7) Модуль
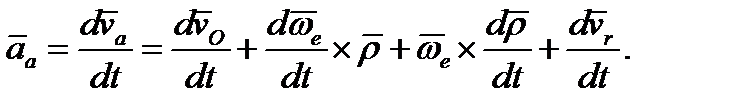
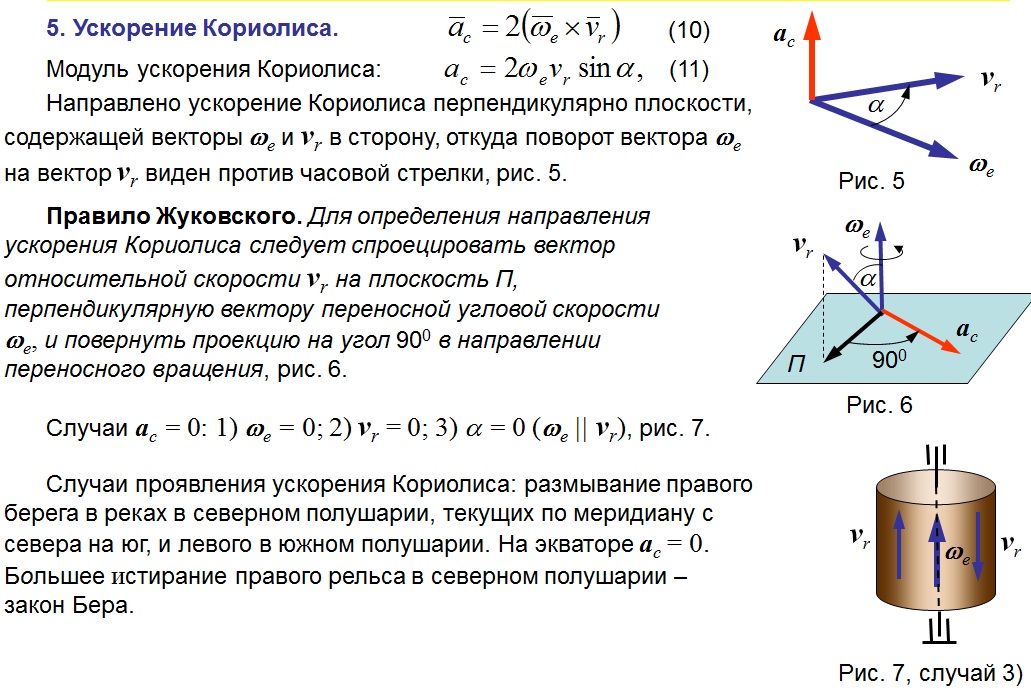 
Date: 2015-09-03; view: 1164; Нарушение авторских прав | Понравилась страница? Лайкни для друзей: |
|
|



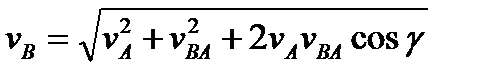 По модулю vBA = w× AB, т.к. вектор w ^пл.Оху, v BA ^ r AB. Таким образом v B = v A + w ´ r AB (2а)
По модулю vBA = w× AB, т.к. вектор w ^пл.Оху, v BA ^ r AB. Таким образом v B = v A + w ´ r AB (2а)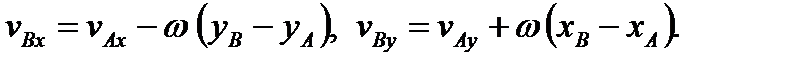
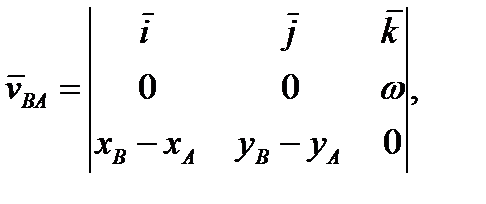 При известным угле g = Р v A, v BA Скорость vB можно также подсчитать, проецируя (2а) на оси координат:
При известным угле g = Р v A, v BA Скорость vB можно также подсчитать, проецируя (2а) на оси координат: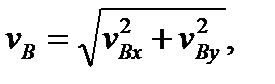
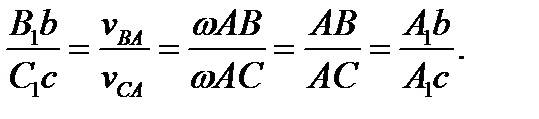 16. Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка. То есть АС/СВ = А1С1/С1В1, рис.6. Построим в точках В и С треугольники скоростей согласно (2). Фигура AA1 cbBCA – параллелограм, как построенная на векторах v A. Отсюда следует, что AC = A1c и BC = bc. Треугольники A1C1c и A1B1b подобны, так как
16. Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка. То есть АС/СВ = А1С1/С1В1, рис.6. Построим в точках В и С треугольники скоростей согласно (2). Фигура AA1 cbBCA – параллелограм, как построенная на векторах v A. Отсюда следует, что AC = A1c и BC = bc. Треугольники A1C1c и A1B1b подобны, так как
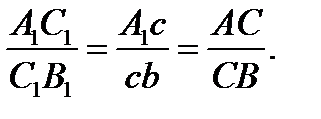 Из подобия треугольников следует
Из подобия треугольников следует 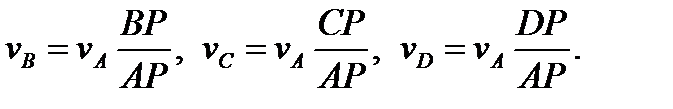
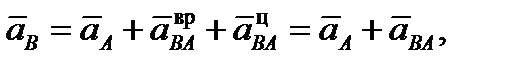
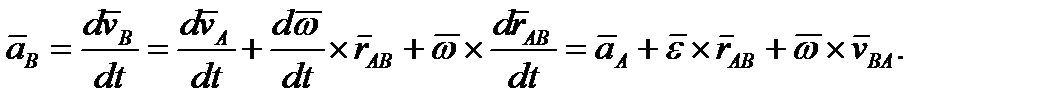 Запишем теорему о скорости некоторой точки фигуры В, v B = v A + w ´ r AB, где vA – скорость полюса А, и продифференцируем ее по времени
Запишем теорему о скорости некоторой точки фигуры В, v B = v A + w ´ r AB, где vA – скорость полюса А, и продифференцируем ее по времени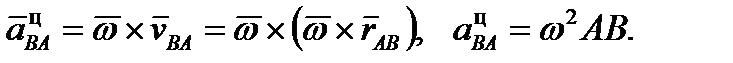
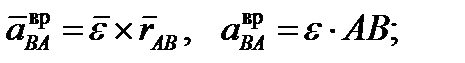 или (1) где
или (1) где 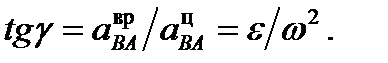
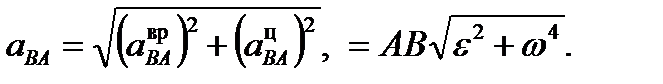 Модуль вращательного ускорения точки В вокруг полюса А (2) Угол g найдется из формулы Вращательное ускорение а ВАвр ^ АВ, центростремительное а ВАцнаправлено от точки В к полюсу А, рис. 1.
Модуль вращательного ускорения точки В вокруг полюса А (2) Угол g найдется из формулы Вращательное ускорение а ВАвр ^ АВ, центростремительное а ВАцнаправлено от точки В к полюсу А, рис. 1.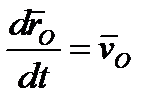 Для любого момента времени имеем, рис.3, r = r O + r (5) Дифференцируя (5) по времени, получим
Для любого момента времени имеем, рис.3, r = r O + r (5) Дифференцируя (5) по времени, получим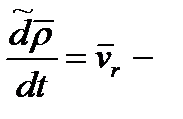
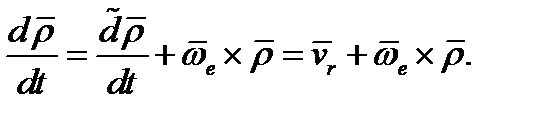 Производная - скорость начала подвижной системы координат О.
Производная - скорость начала подвижной системы координат О.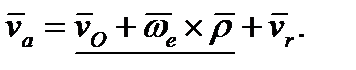 Производная согласно формуле Бура Здесь
Производная согласно формуле Бура Здесь 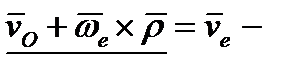 Подчеркнутые слагаемые представляют собой скорость той точки подвижной системы
Подчеркнутые слагаемые представляют собой скорость той точки подвижной системы 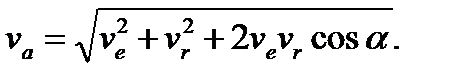 координат, с которой совпадает точка М. Следовательно, переносная скорость точки М. Окончательно
координат, с которой совпадает точка М. Следовательно, переносная скорость точки М. Окончательно 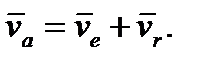 (7) Модуль
(7) Модуль