
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Особенности динамики поля с источниками
|
|
Согласно эксперим. данным, поток электрич. поля Е через S пропорционален суммарному заряду в объёме V:
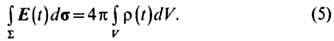
Для неподвижных зарядов это утверждение следует из закона Кулона, но в Э. справедливо и при произвольном движении зарядов внутри поверхности S, несмотря на существование излучения. Тем самым устанавливается (и экспериментально подтверждается) фундам. свойство заряда Q, к-рое может служить новым способом его измерения, формально независимым от старого (1) и не апеллирующим к кинематике заряда.
Этот шаг однозначно определяет ур-ния Э. Действительно, формулировка (5) в дифференц. форме и требование её релятивистской ковариантности, т. е. выполнения при любой скорости движения инерциальной системы отсчёта с учётом преобразований координат, поля, плотностей заряда и тока, приводят к следствию
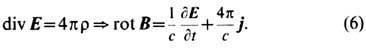
В результате магн. поле можно рассматривать как неизбежный релятивистский результат движения электрич. зарядов (тока j) и нестационарности создаваемого ими электрич. поля (тока смещения д E /дt).
Аналогичная аргументация по отношению к закону сохранения (в частности, отсутствия) магн. зарядов даёт закон эл.-магн. индукции:
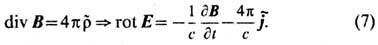
С учётом ур-ний непрерывности j a,a= 0 и 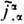 =0 независимыми оказываются только правые ур-ния в (6) и (7). (Об их записи в интегр. форме, о граничных и нач. условиях, условиях излучения и о единственности решения см. Максвелла уравнения.)Полевые ур-ния (6), (7) совместно с ур-ниями движения всех зарядов под действием силы Лоренца лежат в основе Э. В релятивистски ковариантной форме ур-ния (6) и (7) имеют вид:
=0 независимыми оказываются только правые ур-ния в (6) и (7). (Об их записи в интегр. форме, о граничных и нач. условиях, условиях излучения и о единственности решения см. Максвелла уравнения.)Полевые ур-ния (6), (7) совместно с ур-ниями движения всех зарядов под действием силы Лоренца лежат в основе Э. В релятивистски ковариантной форме ур-ния (6) и (7) имеют вид:
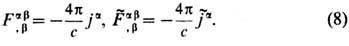
Т. о., электрич. и магн. 4-плотности тока являются локальными источниками полей. Поле, порождённое движущимися зарядами, согласно (8), распространяется в свободное от них пространство независимо от источников с одной и той же скоростью с (рис. 1). Она не зависит также от выбора инерциальной системы отсчёта ввиду явной ковариантности (8). Тем самым Э. предоставляет фактич. основу для второго постулата спец. теории относительности, требующего существования инвариантной скорости распространения сигналов.
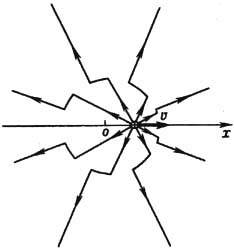
Рис. 1. Силовые линии электрического поля Е заряда q, начавшего двигаться из точки о со скоростью u.
Источники. Вместе с тем скорость u движения зарядов как источников поля в ур-ниях Максвелла формально может быть любой, в частности превышающей скорость света в вакууме [О. Хевисайд (О. Heaviside), 1889; У. Том-сон (W. Thomson), 1901; А. Зоммерфельд (A. Sommerfeld), 1904]. Последняя возможность может быть обеспечена (даже если не иметь в виду гипотетич. тахионы)совокупным движением реальных зарядов под действием разл. "зайчиков", напр. плоских импульсов фотонов, электронов или др. частиц, наклонно падающих на плоский экран, либо под действием "ножниц", где роль "зайчика" играет точка пересечения образующих "ножницы" двух лезвий. В силу неравенства u >c создаваемое "зайчиком" пятно зарядов с плотностью r может отвечать сколь угодно большой плотности тока j = r u.
В подобных и др. случаях, когда движение определённых зарядов допустимо считать заранее известным, в правых частях ур-ний (8) или (6), (7) аддитивно выделяют т. н. сторонние источники j a ст= (c r ст, j ст) и 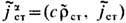 -- заданные в пространстве-времени - 4-плотности тока, для к-рых
-- заданные в пространстве-времени - 4-плотности тока, для к-рых 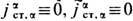
Ограничения. Границы применимости Э. в зависимости от анализируемых реальных ситуаций и преследуемых целей могут определяться самыми различными причинами. Ниже указаны лишь наиболее типичные из них.
Важнейшим свойством ур-ний Максвелла является их линейность: поля, созданные двумя независимыми системами источников j a1ст, 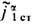 и j a2cт,
и j a2cт, 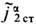 , подчиняются суперпозиции принципу, т. е. сумма этих полей является решением ур-ний при совместном действии источников: j a ст= j a1ст+ j a2ст,
, подчиняются суперпозиции принципу, т. е. сумма этих полей является решением ур-ний при совместном действии источников: j a ст= j a1ст+ j a2ст, 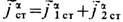 . Нарушение принципа суперпозиции полей происходит за счёт нелинейного возбуждения новых токов j a,
. Нарушение принципа суперпозиции полей происходит за счёт нелинейного возбуждения новых токов j a, 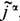 , индуцируемых j a ст,
, индуцируемых j a ст, 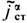 при достаточно сильных полях в среде (либо в вакууме из-за квантовых эффектов рождения и уничтожения частиц, прежде всего электрон-позитронных пар, в полях | F ab|
при достаточно сильных полях в среде (либо в вакууме из-за квантовых эффектов рождения и уничтожения частиц, прежде всего электрон-позитронных пар, в полях | F ab| 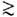 Е с
Е с 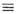 В с = т 2 е с 3 /
В с = т 2 е с 3 / 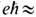 4,4.1013 Гс). Согласно квантовой электродинамике, вследствие рождения пар частица-античастица в достаточно сильных полях и при локализации заряж. частиц (массой т)в области с размерами порядка комптоновской длины волны
4,4.1013 Гс). Согласно квантовой электродинамике, вследствие рождения пар частица-античастица в достаточно сильных полях и при локализации заряж. частиц (массой т)в области с размерами порядка комптоновской длины волны 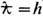 / g тс возникает ограничение и на их макс. плотность тока
/ g тс возникает ограничение и на их макс. плотность тока 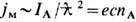 Здесь I А = g тс 3 /е- т. н. ток Аль-вена, отвечающий макс. концентрации
Здесь I А = g тс 3 /е- т. н. ток Аль-вена, отвечающий макс. концентрации 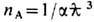 частиц с зарядом е, движущихся прямолинейно друг за другом на расстоянии своего эл.-магн. классич. радиуса e 2 / g mc 2 =
частиц с зарядом е, движущихся прямолинейно друг за другом на расстоянии своего эл.-магн. классич. радиуса e 2 / g mc 2 = 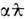 . со скоростью u ~c в трубке с поперечным размером ~
. со скоростью u ~c в трубке с поперечным размером ~ 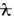 ; g=1/
; g=1/ 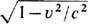 , a= е 2/
, a= е 2/ 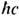 . Для электронов
. Для электронов
I A/g  17 кА.
17 кА.
В соответствии с неопределённостей соотношениями существуют также мин. среднеквадратичные значения полей, к-рые зависят от их частоты со и в свободном пространстве отвечают следующей спектр. плотности энергии нулевых колебаний эл.-магн. поля: [ Е 2(w) + B 2(w)]/8p~ 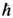 (2/l)3, где l= 2p с /w. При измерении состояния полей E (ct, r), B (ct, r)как ф-ций r и t в области пространства L 3 и времени D t, aтакже при измерении их пространственно-временного среднего по этой области вследствие квантовых эффектов, обусловленных неустранимым обратным влиянием измерит. аппаратуры на поле, возникают абс. ограничения точности D E мин = D В мин = 2
(2/l)3, где l= 2p с /w. При измерении состояния полей E (ct, r), B (ct, r)как ф-ций r и t в области пространства L 3 и времени D t, aтакже при измерении их пространственно-временного среднего по этой области вследствие квантовых эффектов, обусловленных неустранимым обратным влиянием измерит. аппаратуры на поле, возникают абс. ограничения точности D E мин = D В мин = 2 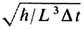 [Л. <Д. <Ландау, Р. Пайерлс (R. Peierls), 1931] (см. также Квантовые неразрушающие измерения).
[Л. <Д. <Ландау, Р. Пайерлс (R. Peierls), 1931] (см. также Квантовые неразрушающие измерения).
Симметрия. При локальных (точечных) преобразованиях координат и времени максимальную Ли группу симметрии, не меняющую вид ур-ний Максвелла с токами (8), составляют наряду с линейными 6-параметрич. преобразованиями Лоренца х a 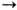 x' a = L ' ba x b не только очевидные 4-параметрич. преобразования сдвига х a
x' a = L ' ba x b не только очевидные 4-параметрич. преобразования сдвига х a  х' a = х a + а a (см. Пуанкаре группа)и 1-параметрич. масштабные преобразования x a
х' a = х a + а a (см. Пуанкаре группа)и 1-параметрич. масштабные преобразования x a  х' a = bх a, но и нелинейные 4-параметрич. конформные преобразования (Н. Bateman, E. Cuningham, 1909)
х' a = bх a, но и нелинейные 4-параметрич. конформные преобразования (Н. Bateman, E. Cuningham, 1909)
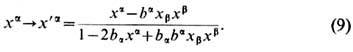
Сопровождающие (9) конформные преобразования полей Е, В и токов j a, 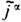 . являются линейными, но явно зависят от х a; они используются при построении нелинейных версий ур-ний Э. и нахождении их точных решений. Ур-ния Максвелла (8) не изменяются также при локальных внутренних, т. е. не затрагивающих пространственно-временные координаты, д у а л ь н ы х п р е о б р а з о в а н и я х:
. являются линейными, но явно зависят от х a; они используются при построении нелинейных версий ур-ний Э. и нахождении их точных решений. Ур-ния Максвелла (8) не изменяются также при локальных внутренних, т. е. не затрагивающих пространственно-временные координаты, д у а л ь н ы х п р е о б р а з о в а н и я х:
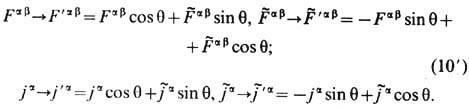
Для свободных полей они известны как 1-параметрич. п р е о б р а з о в а н и я Л а р м о р а-Р а й н и ч а
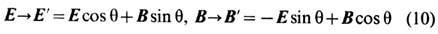
и связаны с поляризац. вырождением эл.-магн. волн. Однако преобразования (10'), как и (9), не сохраняют вид ур-ний движения (1) электрич. (или магн.) зарядов.
Магнитный заряд. Явное согласование дуальной симметрии ур-ний Максвелла и ур-ний движения имеет место только в случае дуально заряженных частиц, несущих одновременно электрич. qn и магн. 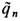 заряды. Последние преобразуются в соответствии с (10') по правилу
заряды. Последние преобразуются в соответствии с (10') по правилу
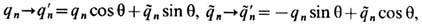
не изменяющему полную силу Лоренца, действующую на n -ю заряж. частицу:
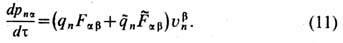
Если отношение 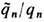 равно одной и той же (любой) величине для всех частиц, то дуальный поворот на угол
равно одной и той же (любой) величине для всех частиц, то дуальный поворот на угол 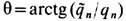 приводит ур-ния Э. (8), (11) к обычной форме без магн. монополей (
приводит ур-ния Э. (8), (11) к обычной форме без магн. монополей (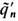 =0) с наблюдаемыми эфф. электрич. зарядами частиц q'n=
=0) с наблюдаемыми эфф. электрич. зарядами частиц q'n= 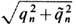 и наблюдаемыми полями E ', В ' из (10) [Л. Пёйдж (L. Page), H. Адам (N. Adam), 1940]. Универсальность отношения
и наблюдаемыми полями E ', В ' из (10) [Л. Пёйдж (L. Page), H. Адам (N. Adam), 1940]. Универсальность отношения 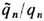 для известных частиц экспериментально подтверждается с большой относит. точностью (напр., для электронов и протонов относит. погрешность не превышает ~10-26). Это обстоятельство, позволяя исключить дуально заряженные частицы и, в частности, "чистый" магн. монополь (для к-рого отношение
для известных частиц экспериментально подтверждается с большой относит. точностью (напр., для электронов и протонов относит. погрешность не превышает ~10-26). Это обстоятельство, позволяя исключить дуально заряженные частицы и, в частности, "чистый" магн. монополь (для к-рого отношение 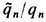 по величине и по знаку должно быть обратно таковому для "чистого" электрич. заряда), скрывает дуальную симметрию однозарядовой Э. Тем не менее и в ней наиб. фундаментальными естественно считать те наблюдаемые, к-рые инвариантны относительно дуальных преобразований (а не сами электрич. и магн. поля), напр. дуально симметричную силу Лоренца (11), эфф. заряд q'n и компоненты T m v тензора плотности энергии-импульса эл.-магн. поля (А. Зоммерфельд, 1928):
по величине и по знаку должно быть обратно таковому для "чистого" электрич. заряда), скрывает дуальную симметрию однозарядовой Э. Тем не менее и в ней наиб. фундаментальными естественно считать те наблюдаемые, к-рые инвариантны относительно дуальных преобразований (а не сами электрич. и магн. поля), напр. дуально симметричную силу Лоренца (11), эфф. заряд q'n и компоненты T m v тензора плотности энергии-импульса эл.-магн. поля (А. Зоммерфельд, 1928):
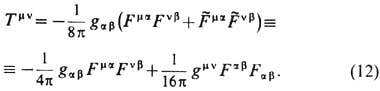
Даже в отсутствие "чистых" магн. монополей в Э. допустимы высшие магн. мультиполи, начиная с диполя, образованные магнитно нейтральной совокупностью монополей (ср. двухкварковую структуру мезонов и трёхквар-ковую структуру барионов). Однако эксперименты фактически исключают эту возможность, показывая, что все магн. мультиполи образованы электрич. токами. Так, в 1951 в экспериментах по рассеянию нейтронов в неоднородном магн. поле В = В (х) у 0 (рис. 2) было показано
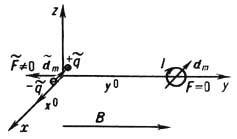
Рис. 2. Силы, действующие на "токовый" dm и "моно польный"  магнитные диполи, ориентированные против оси х° и находящиеся в неоднородном магнит ном поле В=В(х)у°.
магнитные диполи, ориентированные против оси х° и находящиеся в неоднородном магнит ном поле В=В(х)у°.
[К. Г. Шал (С. G. Shull) и др.], что их магн. дипольный момент d m имеет токовую [Ю. Швингер (J. Schwinger), 1937], а не монопольную [Ф. Блох (F. Bloch), 1936] природу: нейтроны движутся под действием силы F = 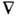 (d m B), характерной для рамки с электрич. током I=c d m/ p r 02. (радиуса r 0), но не силы
(d m B), характерной для рамки с электрич. током I=c d m/ p r 02. (радиуса r 0), но не силы 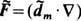 В, характерной для двух. разноимённых монополей b
В, характерной для двух. разноимённых монополей b 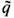 = +
= + 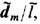 расположенных на расстоянии l. При
расположенных на расстоянии l. При 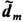 = d m различие указанных сил F -
= d m различие указанных сил F - 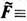 . [ d m rot B ]обусловлено различным взаимодействием диполей со сторонними токами j =(c/ 4p)rot В, создающими неоднородное магн. поле В (r ).
. [ d m rot B ]обусловлено различным взаимодействием диполей со сторонними токами j =(c/ 4p)rot В, создающими неоднородное магн. поле В (r ).
Электромагнитная асимметрия. Т. о., вещество устроено дуально несимметрично, из одних лишь электрич. зарядов. Впрочем, по крайней мере в макроскопич. Э., это не исключает ситуации, когда в неподвижной системе проводников отлична от нуля только плотность тока (и соответствующие магн. и тороидные мультипольные моменты), тогда как плотность электрич. заряда тождественно равна нулю. Создаваемое такой системой электрич. поле Е отлично от нуля, только если токи нестационарны. При движении относительно этой системы наряду с плотностью тока в ней будут наблюдаться плотность заряда и соответствующие электрич. мультипольные моменты; однако не существует системы отсчёта, из к-рой наблюдалась бы одна только плотность заряда и не наблюдалась бы плотность тока, а следовательно, всюду отсутствовало бы магн. поле.
В общем случае, согласно (7), ввиду отсутствия магн. зарядов и независимо от движения электрич. зарядов
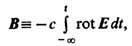
т. е. магн. поле выступает как вспомогательное, характеризующее историю эволюции основного электрич. поля. Несмотря на это, введение самостоят. магн. поля необходимо, если последовательно придерживаться идеи близ-кодействия зарядов, т. е. описывать их взаимодействие только посредством локально (а не интегрально) измеримых полевых величин.
Экстремальные принципы. В отличие от дуально симметричной Э. (8), (11), в однозарядовой Э. не возникает проблем с получением совместной системы ур-ний (1), (8) 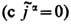 для движения отд. электрич. зарядов qn и поля в вакууме из вариац. принципа (см. Вариационное исчисление). Для удобства вводятся новые полевые переменные - скалярный j(сt, r) и векторный A (ct, r) потенциалы электромагнитного поля:
для движения отд. электрич. зарядов qn и поля в вакууме из вариац. принципа (см. Вариационное исчисление). Для удобства вводятся новые полевые переменные - скалярный j(сt, r) и векторный A (ct, r) потенциалы электромагнитного поля:
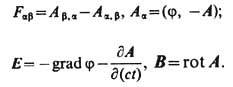 (13)
(13)
Тогда второе ур-ние из (8), принимающее вид F ab, v + Fv a,b+ + F b v ,a = 0, и, следовательно, ур-ния (7) с 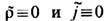 удовлетворяются тождественно. Первое же ур-ние из (8) и ур-ние (1') с учётом (4') [или ур-ния (6) и ур-ние (1) с учётом (4)] есть в точности Эйлера - Лагранжа уравнения с лагранжианом
удовлетворяются тождественно. Первое же ур-ние из (8) и ур-ние (1') с учётом (4') [или ур-ния (6) и ур-ние (1) с учётом (4)] есть в точности Эйлера - Лагранжа уравнения с лагранжианом
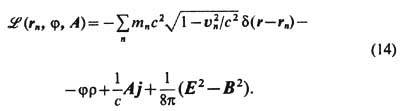
При этом, правда, в последнем слагаемом необходимо исключить бесконечную энергию собственного (кулонов-ского) поля точечных зарядов, а в слагаемом взаимодействия A a j a /c- самовоздействие зарядов. Поскольку наблюдаемая масса заряж. частиц т n конечна, компенсацию их бесконечной эл.-магн. массы следует обеспечить введением бесконечной отрицат. массы неэлектромагн. происхождения ("перенормировка" массы). Эта непоследовательность, связанная с идеализацией точечных элементарных частиц, в релятивистской классич. физике, не включающей описание детальной внутр. структуры заряж. частиц, напр. как полевых образований, неизбежна в силу невозможности существования абсолютно недеформируемых протяжённых тел.
Калибровочная инвариантность. Если отказаться от то-чечности и учесть неэлектромагн. взаимодействие частиц, то, описывая частицы нек-рым классич. полем y, первое слагаемое в (14) следует заменить на более общий лагранжиан частиц 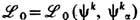 , зависящий от к.-л. многокомпонентных комплексных ф-ций y k (x a), k= 1, 2,..., и их производных y k ,a. С учётом вещественности
, зависящий от к.-л. многокомпонентных комплексных ф-ций y k (x a), k= 1, 2,..., и их производных y k ,a. С учётом вещественности 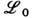 требование инвариантности полного лагранжиана относительно локальных фазовых преобразований
требование инвариантности полного лагранжиана относительно локальных фазовых преобразований
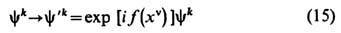
(калибровочные преобразования;  обнаруживает за-мечат. факт, известный как эвристич. принцип калибровочной инвариантности и перенесённый из Э. на всю теорию поля [Ч. Янг (Ch. Yang), P. Миллс (R. Mills), 1953; M. Гелл-Ман (М. Gell-Mann), 1956]. Согласно этому принципу, инвариантность исходного лагранжиана
обнаруживает за-мечат. факт, известный как эвристич. принцип калибровочной инвариантности и перенесённый из Э. на всю теорию поля [Ч. Янг (Ch. Yang), P. Миллс (R. Mills), 1953; M. Гелл-Ман (М. Gell-Mann), 1956]. Согласно этому принципу, инвариантность исходного лагранжиана 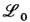 восстанавливается удлинением производных
восстанавливается удлинением производных
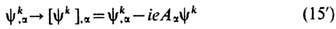
за счёт введения компенсирующего поля A a(х b), преобразующегося одновременно с (15) по т. н. калибровочному закону

не меняющему наблюдаемые компоненты поля (13) F ab. [В (15') величина заряда электрона е выступает как константа введённого таким образом взаимодействия - мин. эл.-магн. взаимодействия,- давая ещё одно неявное определение электрич. заряда.] Если для определённости ограничиться линейной зависимостью 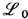 от производных y k ,a, характерной для спинорных полей вещества, то в полном лагранжиане
от производных y k ,a, характерной для спинорных полей вещества, то в полном лагранжиане
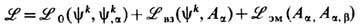
непосредственно возникает необходимый лагранжиан взаимодействия 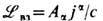 вместе с новым определением 4-плотности тока
вместе с новым определением 4-плотности тока 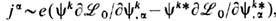 , не связанным с точечностью зарядов [ср. (4), (14)].
, не связанным с точечностью зарядов [ср. (4), (14)].
Собственный лагранжиан компенсирующего (здесь - эл.-магнитного) поля выбирается в простейшем виде 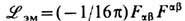 [см. (3), (13)], обеспечивающем его инвариантность при калибровочном преобразовании (15 ") в отсутствие вещества. Этим, в частности, исключается слагаемое вида
[см. (3), (13)], обеспечивающем его инвариантность при калибровочном преобразовании (15 ") в отсутствие вещества. Этим, в частности, исключается слагаемое вида 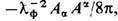 а следовательно, возможность ненулевой массы фотона
а следовательно, возможность ненулевой массы фотона 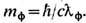 Наличие ненулевой массы фотона кардинально меняло бы законы Э. на расстояниях
Наличие ненулевой массы фотона кардинально меняло бы законы Э. на расстояниях 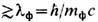 [Л. де Бройль (L. de Broglie), 1924]; однако земные эксперименты, в частности по проверке закона Кулона и независимости скорости эл.-магн. волн в вакууме от их частоты, допускают такую возможность только на расстояниях
[Л. де Бройль (L. de Broglie), 1924]; однако земные эксперименты, в частности по проверке закона Кулона и независимости скорости эл.-магн. волн в вакууме от их частоты, допускают такую возможность только на расстояниях 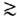 1010 см, а наблюдения стабильных конфигураций газа и магн. полей галактик - на расстояниях
1010 см, а наблюдения стабильных конфигураций газа и магн. полей галактик - на расстояниях 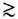 1022 см. В принципе было бы возможно также несохранение электрич. заряда, напр. распад электрона на нейтральные частицы или осцилляции электрон <-> позитрон, хотя подобные процессы и подавлены неизбежным участием большого кол-ва (
1022 см. В принципе было бы возможно также несохранение электрич. заряда, напр. распад электрона на нейтральные частицы или осцилляции электрон <-> позитрон, хотя подобные процессы и подавлены неизбежным участием большого кол-ва (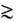 1013 -1021) сверхмягких продольных фотонов (Я. Б. Зельдович, Л. Б. Окунь, М. Б. Волошин, 1978); однако лабораторные эксперименты и глобальные геоэлектрич. оценки показывают, что время жизни электрич. заряда превышает 1030 с.
1013 -1021) сверхмягких продольных фотонов (Я. Б. Зельдович, Л. Б. Окунь, М. Б. Волошин, 1978); однако лабораторные эксперименты и глобальные геоэлектрич. оценки показывают, что время жизни электрич. заряда превышает 1030 с.
Внутренние противоречия (неклассические проблемы)
Нелинейность. Включение в лагранжиан эл.-магн. поля неквадратичных по E и В слагаемых ведёт к нелинейной теории. Наиб. известное нелинейное обобщение Э. развито В. Гейзенбергом (W. Heisenberg), Г. Эйлером (Н. Euler), В. Вайскопфом (V. Weisskopf) (1936) и Ю. Швингером (1951) на основе квантово-электродинамич. вычисления поляризации электрон-позитронного вакуума, создаваемой достаточно плавными в пространстве-времени полями, для к-рых удаётся использовать точное решение Дирака уравнения. Соответствующий лагранжиан, для простоты выписываемый в естеств. единицах (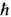 =с= 1),
=с= 1),
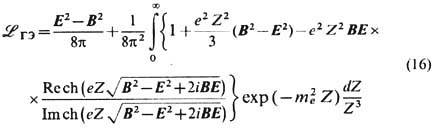
описывает только эл.-магн. поле, причём плавно неоднородное, в пренебрежении производными от инвариантов (3). Он не претендует на самосогласованное "эл.-магн." описание источников поля - электронов и позитронов с зарядами + е и конечной классич. массой т е, как это предполагалось в нек-рых моделях, напр. М. Борном (М. Born) и Л. Инфельдом (L. Infeld) (1934), выбиравшими лагранжиан в виде
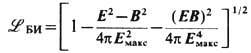
(впрочем, более реалистичном с точки зрения совр. струн теории; Е. С. Фрадкин, А. А. Цейтлин, 1985). Здесь E макс -нек-рое макс. поле. Мнимая часть (16) характеризует неустойчивость вакуума, точнее, вероятность рождения электрон-позитронных пар в единичном объёме за единицу времени, значительную при 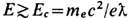 и убывающую по закону ехр(- p Е с/Е)в полях Е<<Е c. Вещественная часть (16) отвечает за собственную нелинейность "классич." электрон-позитронного вакуума-в отсутствие др. частиц и др. взаимодействий, к-рые, конечно, кардинально меняют ситуацию, скрадывая чисто эл.-магн. взаимодействие, начиная с расстояний ~10-13 см (сильное) и особенно ~ 10-16 см (электрослабое).
и убывающую по закону ехр(- p Е с/Е)в полях Е<<Е c. Вещественная часть (16) отвечает за собственную нелинейность "классич." электрон-позитронного вакуума-в отсутствие др. частиц и др. взаимодействий, к-рые, конечно, кардинально меняют ситуацию, скрадывая чисто эл.-магн. взаимодействие, начиная с расстояний ~10-13 см (сильное) и особенно ~ 10-16 см (электрослабое).
Если, несмотря на сказанное, обратиться, напр., к модификации закона Кулона, т. е. к сферич. симметрич. решению D = q/r 2 соответствующих (16) электростатич. ур-ний Максвелла div D = 0 (при r 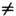 0),
0), 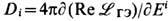 , с сингулярностью (точечным зарядом q)в начале координат r = 0, то обнаружится принципиальная роль нелинейности вакуума:
, с сингулярностью (точечным зарядом q)в начале координат r = 0, то обнаружится принципиальная роль нелинейности вакуума:
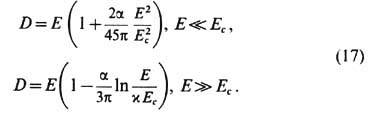
Здесь число  учитывает все члены первого порядка по постоянной тонкой структуры
учитывает все члены первого порядка по постоянной тонкой структуры 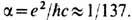 Согласно (17), на больших расстояниях поле Е ослабляется по сравнению с g/r 2: D/E > 1, т. е. поляризов. вакуум экранирует "голый" заряд q. Однако на малых расстояниях эта экранировка уменьшается, и поляризация вакуума меняет знак при
Согласно (17), на больших расстояниях поле Е ослабляется по сравнению с g/r 2: D/E > 1, т. е. поляризов. вакуум экранирует "голый" заряд q. Однако на малых расстояниях эта экранировка уменьшается, и поляризация вакуума меняет знак при 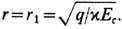 На меньших расстояниях возникает антиэкранировка, причём отношение D/E принимает мин. значение a/3pпри
На меньших расстояниях возникает антиэкранировка, причём отношение D/E принимает мин. значение a/3pпри
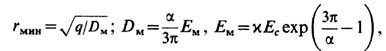
когда ф-ция D(E)достигает максимума и обнаруживающаяся двузначность ф-ции Е(r)делает физически бессмысленным анализ области r < r мин. Хотя сама квантовая Э. как асимптотическая по a теория вряд ли верна на расстояниях r<<r мин, апри r ~ r мин указанное решение ввиду пространственной неоднородности заведомо выходит за квантово-электродинамич. рамки применимости лагранжиана (16), утверждение о том, что в нелинейной Э. (даже без учёта рождения реальных электрон-позитронных пар) должны существовать макс. электростатич. поле Е м и аналогичное макс. магнитостатич. поле В м = В с ехр (3p/a - 1), представляется неизбежным, поскольку остаётся справедливым и для пространственно однородного поля, напр. в плоском конденсаторе или в соленоиде [М. Гринман (М. Greenman), Ф. Рорлих (F. Rohrlich), 1973; Д. А. Киржниц, А. <Д. Линде, 1978]. Это ещё раз показывает, что наивные представления о точечности заряда, напр. электрона, отвечающие неограниченному при r 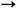 0 кулоновскому полю е/r 2, противоречивы, причём не только в Э., но и в квантовой Э. (Л. Д. Ландау, И. Я. По-меранчук, Е. С. Фрадкин, 1955). Наблюдаемая величина (и масса) заряда так или иначе должна определяться самосогласованными свойствами поляризов. вакуума с учётом неэлектромагн. взаимодействий, "размазывающих" точечный заряд.
0 кулоновскому полю е/r 2, противоречивы, причём не только в Э., но и в квантовой Э. (Л. Д. Ландау, И. Я. По-меранчук, Е. С. Фрадкин, 1955). Наблюдаемая величина (и масса) заряда так или иначе должна определяться самосогласованными свойствами поляризов. вакуума с учётом неэлектромагн. взаимодействий, "размазывающих" точечный заряд.
Классический размер частиц. При этом в любой, в т. ч. квантовой, теории, отвлекающейся от неэлектромагн. структуры заряда, введение представлений о нелокальном взаимодействии поля с протяжённой заряж. частицей как единым целым наталкивается на значит. трудности, прежде всего причинного характера. В Э., пусть линейной (14), подобные попытки, несмотря на содержательность, также оказываются ограниченными. Среди них наиб. популярно представление о распределении заряда электрона по области размером ~r е = е 2/т е с 2 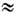 3.10-13 см (классический радиус электрона), что соответствует приписыванию, хотя бы частичному, энергии покоя электрона т е с 2. его кулоновскому полю. Это представление, конечно, предполагает наличие к.-л. неэлектромагн., упругих сил (т. н. н а т я ж ен и й П у а н к а р е), к-рые препятствуют кулоновскому расталкиванию "частей" электрона и обеспечивают релятивистскую ковариантность его полного 4-импульса, складывающегося из нековариантных 4-импульсов поля "электрич. начинки" и натяжений "упругого теста". Анализ устройства натяжений Пуанкаре выходит за рамки Э. не только из-за неизбежности квантового подхода, но даже потому, что внутри такого электрона они благодаря классич. эффектам гравитации, по-видимому, обусловливают наличие отрицат. плотности массы покоя [В. Боннор (W. Bonnor) и др., 1989].
3.10-13 см (классический радиус электрона), что соответствует приписыванию, хотя бы частичному, энергии покоя электрона т е с 2. его кулоновскому полю. Это представление, конечно, предполагает наличие к.-л. неэлектромагн., упругих сил (т. н. н а т я ж ен и й П у а н к а р е), к-рые препятствуют кулоновскому расталкиванию "частей" электрона и обеспечивают релятивистскую ковариантность его полного 4-импульса, складывающегося из нековариантных 4-импульсов поля "электрич. начинки" и натяжений "упругого теста". Анализ устройства натяжений Пуанкаре выходит за рамки Э. не только из-за неизбежности квантового подхода, но даже потому, что внутри такого электрона они благодаря классич. эффектам гравитации, по-видимому, обусловливают наличие отрицат. плотности массы покоя [В. Боннор (W. Bonnor) и др., 1989].
Строго говоря, вследствие эффекта рождения электрон-позитронных пар применимость Э., по крайней мере без учёта сильных флуктуации заряда и эл.-магн. поля, проблематична уже на расстояниях меньше комптоновской длины волны электрона 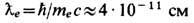 (П. Дирак, 1928). Вместе с тем эксперименты с электронами и мю-онами высоких энергий показывают, что при разл. взаимодействиях с др. частицами они ведут себя как точечные вплоть до расстояний ~10-16 см.
(П. Дирак, 1928). Вместе с тем эксперименты с электронами и мю-онами высоких энергий показывают, что при разл. взаимодействиях с др. частицами они ведут себя как точечные вплоть до расстояний ~10-16 см.
Реакция излучения (радиационное трение). Принимая тем не менее к.-л. распределение заряда, напр. равномерное внутри шара радиуса r е, на основе Э. можно ответить на важнейший вопрос о результате эл.-магн. воздействия разл. "частей" электрона друг на друга. Оказывается, несмотря на то, что эл.-магн. масса зависит от выбранного распределения, от него не зависит самовоздействие электрона, т. е. полная сила реакции излучения [X. Лоренц (Н. Lorentz), 1892; М. Абрагам (М. Abragam), 1904]
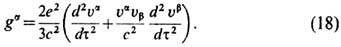
Она получается после перенормировки массы в первом порядке разложения по малому отношению r е к характерному масштабу неоднородности поля (или малому параметру запаздывания e 2 /mec 3 t). Независимость (18) от r е обеспечивает корректность учёта самовоздействия в пределе точечного заряда r е  0. При этом обычно требуется условие малости силы g a по сравнению с силой Лоренца (1') со стороны внеш. поля. Оказывается, что последнее условие достаточно выполнить в системе отсчёта, где электрон покоится и сила реакции излучения на него равна g = (gi/c) =( 2 e 2 / 3 c 3 )d 2 u /dt 2. Для гармонич. полей Е, В с частотой w оно даёт ограничения (условия внутр. непротиворечивости Э.)
0. При этом обычно требуется условие малости силы g a по сравнению с силой Лоренца (1') со стороны внеш. поля. Оказывается, что последнее условие достаточно выполнить в системе отсчёта, где электрон покоится и сила реакции излучения на него равна g = (gi/c) =( 2 e 2 / 3 c 3 )d 2 u /dt 2. Для гармонич. полей Е, В с частотой w оно даёт ограничения (условия внутр. непротиворечивости Э.)
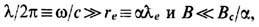
к-рые в a-1 = 137 раз слабее, чем-приведённые выше квантово-электродинамич. ограничения. Второй закон Ньютона для изменения 4-импульса тс ua точечного заряда, находящегося под действием "обычной" внешней силы (1') и "необычной" силы Лоренца-Абрагама (18), к-рая сама определяется кинематикой заряж. частицы, можно представить в более традиционной форме
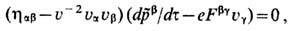
если ввести понятие "эл.-магн." комплекса с эфф. 4-им-пульсом
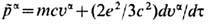
[К. Тейтелбойм (С. Teitelboim), 1970]. Последний указывает на неразделимость заряда и его собственного ближнего поля (эл.-магн. шубы). Это "связанное" поле автоматически учитывается в локальном балансе 4-импульсов, следующем из приведённого второго закона Ньютона: приращение 4-импульса комплекса и создание 4-импульса "свободного" поля излучения происходят за счёт поглощения 4-импульса внешнего поля.
Непротиворечивое введение самовоздействия путём добавления силы (18) к силе Лоренца (I) для каждого точечного ускоренно движущегося заряда qn в рамках Э. предполагает дополнит, условие отсутствия ускорений в областях вне поля, E = B = 0. в (1). Иначе в получающихся ур-ниях движения, содержащих теперь третьи производные координат частиц r n по времени, могли бы появиться неприемлемые решения, отвечающие неогранич. самоускорению заряда за счёт бесконечной энергии собственного поля. Разумеется, упомянутый выше "одетый" эл.-магн. комплекс вообще не испытывает самоускорения, поскольку в любой мгновенно сопутствующей системе отсчёта для перенормированного импульса 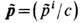 справедливо ур-ние (1). Автоматич. отбор физически приемлемых решений ур-ний движения "голой" заряженной частицы, независимо от соотношения между силой реакции излучения и силой Лоренца, возможен также при их формулировке в эквивалентном интегральном виде, включающем начальные и конечные условия (Ф. Рорлих, 1961), Так, рассматривая (для простоты) нерелятивистский случай [Д. Д. Ива-ненко, А. А. Соколов, 1948; Р. Хааг (R. Haag), 1955], при конечном условии d u /dt= 0 (при
справедливо ур-ние (1). Автоматич. отбор физически приемлемых решений ур-ний движения "голой" заряженной частицы, независимо от соотношения между силой реакции излучения и силой Лоренца, возможен также при их формулировке в эквивалентном интегральном виде, включающем начальные и конечные условия (Ф. Рорлих, 1961), Так, рассматривая (для простоты) нерелятивистский случай [Д. Д. Ива-ненко, А. А. Соколов, 1948; Р. Хааг (R. Haag), 1955], при конечном условии d u /dt= 0 (при  ) имеем
) имеем
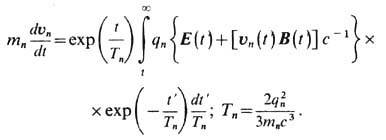
Здесь налицо формальное нарушение причинности, поскольку ускорение выражается не через прошлое, а через будущее движение частицы, т. е. определяется полями, до к-рых частица ещё не дошла, на временном интервале ~ Т n. Однако для всех заряж. частиц (тел) времена Т n = 2 r п/ 3 с <= Т е= 2 е 2 / (3 т е с 3) 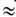 6.10-24 с и, следовательно, все соответствующие проблемы непричинности и нелокальности эл.-магн. взаимодействия оказываются за пределами применимости Э. А именно, принципиальным становится учёт квантовых флуктуации движения электрона (или любой заряж. частицы), для к-рых характерный временной,
6.10-24 с и, следовательно, все соответствующие проблемы непричинности и нелокальности эл.-магн. взаимодействия оказываются за пределами применимости Э. А именно, принципиальным становится учёт квантовых флуктуации движения электрона (или любой заряж. частицы), для к-рых характерный временной, 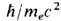 , и пространственный,
, и пространственный, 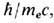 масштабы в
масштабы в 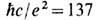 раз больше соответственно временного, Т е, и пространственного, сТ е, масштабов самоускоряющихся решений. Эти проблемы корректно разрешаются при кван-тово-электродинамич. анализе самовоздействия [Е. Мо-ниц, Д. Шарп (Е. Moniz, D. Sharp), 1977; В. К. Кривицкий, В. Н. Цытович, 1991 ]. Оказывается, что при достаточно длительном действии сила реакции излучения действительно проявляется на классич. уровне, напр., она обусловливает спиральное (скручивающееся) движение электронов в однородном магн. поле, отличающееся от винтового движения с постоянным радиусом благодаря трению о собственное синхротронное излучение.
раз больше соответственно временного, Т е, и пространственного, сТ е, масштабов самоускоряющихся решений. Эти проблемы корректно разрешаются при кван-тово-электродинамич. анализе самовоздействия [Е. Мо-ниц, Д. Шарп (Е. Moniz, D. Sharp), 1977; В. К. Кривицкий, В. Н. Цытович, 1991 ]. Оказывается, что при достаточно длительном действии сила реакции излучения действительно проявляется на классич. уровне, напр., она обусловливает спиральное (скручивающееся) движение электронов в однородном магн. поле, отличающееся от винтового движения с постоянным радиусом благодаря трению о собственное синхротронное излучение.
Запаздывание. Причинности принцип играет в Э. важнейшую роль, поскольку, согласно условиям излучения (при постановке нач. задачи в ограниченной области пространства), он требует ограничиться только запаздывающими решениями ур-ний Максвелла, нарушая их обратимость во времени (при замене j 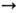 - j, r
- j, r  r, В
r, В  - В, Е -> Е Если для определённости выбрать условие калибровки Лоренца Aa,a= 0, то вынужденное решение соответствующего (8) волнового ур-ния Аa,b,b = 4pja/ с для системы точечных зарядов можно записать в виде
- В, Е -> Е Если для определённости выбрать условие калибровки Лоренца Aa,a= 0, то вынужденное решение соответствующего (8) волнового ур-ния Аa,b,b = 4pja/ с для системы точечных зарядов можно записать в виде
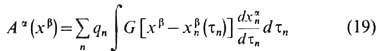
(Льенара - Вихерта потенциалы). Здесь интегрирование ведётся по собств. времени т„ каждой из заряж. частиц и использована запаздывающая Грина функция G(хm)отличная от нуля только в световом конусе будущего (х0>0) и равная там 2d (- хm хm)(для свободного пространства). Из решения (19) вытекают, по существу, все результаты Э. об излучении и взаимодействии зарядов; для пространственно ограниченных задач в нём необходимо лишь соответствующим образом изменить ф-цию Грина.
Дальнодействие. Можно совсем не вводить распределённое в пространстве поле, а подставить его явные значения в точках нахождения зарядов в ур-ния их движения. Тогда Э. примет вид теории прямого межчастичного взаимодействия с ф-цией Лагранжа, зависящей только от координат и скоростей зарядов [X. Тетроде (Н. Tetrode), 1922; А. Фок-кер (A. Fokker), 1929]. Для такой переформулировки Э. в решении (19) удобнее использовать непричинную ф-цию Грина, всюду определяемую полуразностью запаздывающего и опережающего потенциалов:
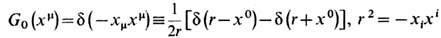
(для свободного пространства). В полевой трактовке этим учитывалось бы "свободное" поле излучения и снималась бы проблема самовоздействия и перенормировки массы в пределе точечных зарядов (П. Дирак, 1938). Вместе с тем добавлением к получающейся ф-ции Лагранжа полных производных по времени удаётся придать новой теории явно причинную форму, причём симметричную по перестановкам частиц [Р. Муре (R. Moore), Т. Скотт (Т. Scott), М. Монахан (М. Monahan), 1988]. В частности, для заряда qk, взаимодействующего со всеми остальными зарядами Вселенной, ф-ция Лагранжа принимает вид:
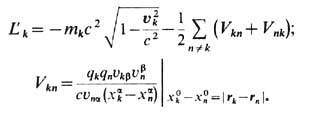
Поправка на силу реакции излучения (в нерелятивистском случае)
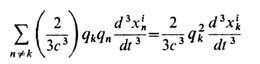
к запаздывающей силе Лоренца, 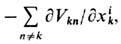 обусловлена одними и теми же (остальными, п
обусловлена одними и теми же (остальными, п  k)зарядами Вселенной и возникает в уравнении движения
k)зарядами Вселенной и возникает в уравнении движения 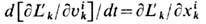 естеств. образом из требования самосогласованности движения всех заряж. частиц при условии квазинейтральности Вселенной и отсутствия элек-трич. поляризации при усреднении по всем рассматриваемым зарядам,
естеств. образом из требования самосогласованности движения всех заряж. частиц при условии квазинейтральности Вселенной и отсутствия элек-трич. поляризации при усреднении по всем рассматриваемым зарядам, 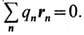 Здесь проблема самоускорения
Здесь проблема самоускорения
заряда не возникает, поскольку отсутствует внутренний бесконечный источник энергии (собственное кулоновское поле), и без силы Лоренца невозможно появление "силы реакции излучения", автоматически низведённой на роль поправки.
Что касается свойств необратимости во времени и выделения обычных запаздывающих решений, то они связываются со свойствами эволюционирующей материи и всей Вселенной и ввиду наличия неэлектромагн. сил выходят за рамки Э., требуя включения дополнит. физ. постулатов [Дж. Уилер (J. Wheeler), P. Фейнман (R. Feynman), 1945; Д. Пегг (D. Pegg), 1975]. В целом исследования Э. как теории прямого межчастичного взаимодействия направлены на то, чтобы преодолеть внутр. противоречия полевой Э., связанные с точечностью зарядов, перенормировкой их массы, нарушением причинности при самовоздействии, ограничением макс. потенциалов и мин. расстояний взаимодействия зарядов и пр. Однако, поскольку эти противоречия затрагивают лишь область квантовых явлений, применение в области классич. физики переформулированной, неполевой Э. оказывается несколько искусственным и непопулярным, особенно вследствие её усложнённости. Последнее гл. обр. обусловлено необходимостью выделения запаздывающих координат частиц, накладывающего сложные условия связи на вариац. ур-ния теории.
Date: 2015-09-03; view: 292; Нарушение авторских прав