
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Работа и мощность силы, приложенной к твердому телу
|
|
Рассмотрим формулы для определения работы и мощности силы, приложенной в какой-либо точке твердого тела, совершающего поступательное или вращательное движение.
1. Работа и мощность силы, приложенной к твердому телу, совершающему поступательное движение.
Рассмотрим твердое тело, совершающее поступательное движение по отношению к инерциальной системе отсчета под действием силы 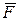 , приложенной в произвольной точке
, приложенной в произвольной точке 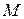 (рис. 24).
(рис. 24).
В случае поступательного движения твердого тела все его точки движутся со скоростями одинаковыми по величине и направлению. Обозначим скорость тела 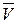 .
.
Используя формулу (4.31), получим
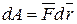 , (4.49)
, (4.49)
где 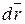 - дифференциал радиус-вектора
- дифференциал радиус-вектора 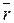 произвольной точки твердого тела
произвольной точки твердого тела 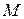 .
.

Рис. 24. Поступательное движение твердого тела под действием силы 
Поделив (4.49) на dt, получим выражение для определения мощности силы, действующей на тело, совершающее поступательное движение:
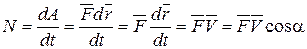 , (4.50)
, (4.50)
где 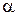 - угол между векторами силы
- угол между векторами силы 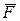 скорости
скорости 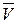 .
.
То есть мощность силы при поступательном движении твердого тела определяется как скалярное произведение вектора силы 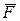 на вектор скорости твердого тела
на вектор скорости твердого тела 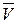 .
.
Интегрируя (4.49) на каком-либо конечном перемещении точки M из начального положения М 0 в положение М 1, получим полную работу силы, действующей на тело на этом перемещении
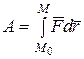 . (4.51)
. (4.51)
2. Работа и мощность силы, приложенной к твердому телу, совершающему вращательное движение.
Рассмотрим вращение твердого тела вокруг неподвижной вертикальной оси Oz под действием силы 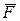 , приложенной в произвольной точке этого тела М (рис. 25).
, приложенной в произвольной точке этого тела М (рис. 25).

Рис. 25. Вращение твердого тела вокруг неподвижной оси
Положение точки М в осях Oxyz определяется радиус-вектором 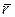 . Скорость точки М направлена по касательной к траектории движения (окружность с центром на оси вращения). Вектор этой скорости можно определить по векторной формуле Эйлера, известной из курса кинематики твердого тела
. Скорость точки М направлена по касательной к траектории движения (окружность с центром на оси вращения). Вектор этой скорости можно определить по векторной формуле Эйлера, известной из курса кинематики твердого тела
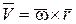 , (4.52)
, (4.52)
где 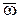 - вектор угловой скорости вращения твердого тела.
- вектор угловой скорости вращения твердого тела.
Используя формулу (4.32), получим
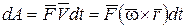 .
.
Меняя в круговом порядке сомножители в смешанном векторном произведении, получим
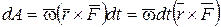 ,
,
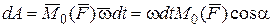 ,
,
где 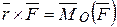 - векторный момент силы
- векторный момент силы 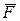 , относительно центра O.
, относительно центра O.
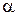 - угол между векторами момента
- угол между векторами момента 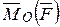 и угловой скорости
и угловой скорости 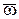 .
.
Учитывая, что:
1. 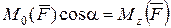 - момент силы
- момент силы 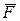 , относительно оси вращения Oz.
, относительно оси вращения Oz.
2.  и следовательно
и следовательно 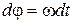 ,
,
окончательно получим
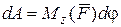 . (4.53)
. (4.53)
Таким образом, элементарная работа силы, приложенной в какой-либо точке твердого тела, вращающегося вокруг неподвижной оси, равна произведению момента этой силы относительно оси вращения на дифференциал угла поворота тела.
Для определения полной работы силы при повороте тела на угол φ, проинтегрировав выражение (4.53), получим
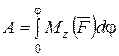 . (4.54)
. (4.54)
В случае когда 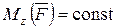 , полную работу можно определить по формуле
, полную работу можно определить по формуле
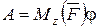 , (4.55)
, (4.55)
где φ – угол поворота тела, на котором определяют работу силы.
Если направление момента 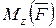 и угловой скорости
и угловой скорости 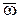 совпадают, то работа силы считается положительной, в противном случае – отрицательной.
совпадают, то работа силы считается положительной, в противном случае – отрицательной.
Определим мощность силы при вращении твердого тела вокруг оси. Используя формулу (4.40), получим
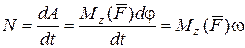 . (4.56)
. (4.56)
То есть мощность силы, приложенной к вращающемуся твердому телу, определяется как произведение момента силы относительно оси вращения на угловую скорость тела. Знак мощности определяется аналогично знаку работы.
| <== предыдущая | | | следующая ==> |
| Работа линейной силы упругости | | | Работа внутренних сил твердого тела |
Date: 2015-09-03; view: 5699; Нарушение авторских прав