Момент силы

Это векторная величина, определяется по формуле

Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак "+", если против часовой, тогда знак "-".

Момент силы реакции опоры отрицательный, так как сила реакции опоры "поворачивает" тело против часовой стрелки

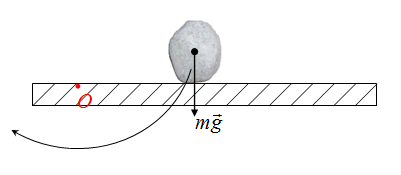
Момент силы тяжести положительный, так как сила тяжести "поворачивает" тело по часовой стрелки

Если точка О выбрана на теле

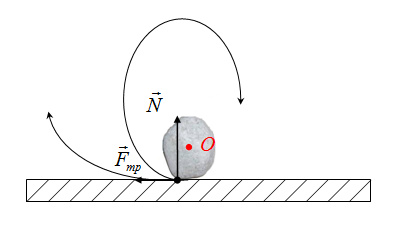
Момент силы реакции опоры и силы трения положительные, так как силы "поворачивают" тело по часовой стрелки

10 теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции 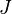тела относительно произвольной оси равен сумме момента инерции этого тела 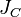относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела 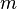на квадрат расстояния 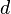между осями:

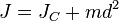
где

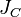— известный момент инерции относительно оси, проходящей через центр масс тела,

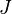— искомый момент инерции относительно параллельной оси,

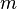— масса тела,

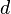— расстояние между указанными осями.

ВЫВОД

Момент инерции, по определению:

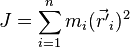
Радиус-вектор 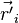можно расписать как сумму двух векторов:

,

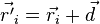где 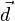— радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

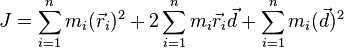
Вынося за сумму 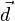, получим:

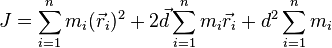
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

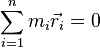
Тогда:

Откуда и следует искомая формула:

,

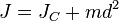где 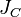— известный момент инерции относительно оси, проходящей через центр масс тела.

ПРИМЕР

Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью ) равен

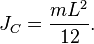
Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен

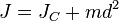
где 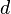— расстояние между искомой осью и осью . В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле :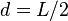

Date: 2015-09-03; view: 504; Нарушение авторских прав