
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Схемы логически правильных рассуждений
|
|
Теория.
Схемы логически правильных рассуждений:
1. Правило заключения – утверждающий модус (Modus Ponens):
"Если из высказывания А следует высказывание В и справедливо (истинно) высказывание А, то справедливо В ". Обозначается:
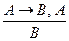 .
.
2. Правило отрицания – отрицательный модус (Modus Tollens):
"Если из А следует В, но высказывание В неверно, то неверно А ":
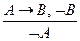 .
.
3. Правила утверждения-отрицания (Modus Ponendo-Tollens):
"Если справедливо или высказывание А, или высказывание В (в разделительном смысле) и истинно одно из них, то другое ложно":
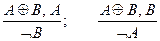 .
.
4. Правила отрицания-утверждения (Modus Tollen-Ponens):
а) "Если истинно или А, или В (в разделительном смысле) и неверно одно из них, то истинно другое":
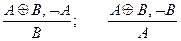 .
.
б) "Если истинно А или В (в неразделительном смысле) и неверно одно из них, то истинно другое":
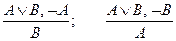 .
.
5. Правило транзитивности (упрощенное правило силлогизма):
"Если из А следует В, а из В следует С, то из А следует С":
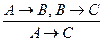 .
.
6. Правило противоречия:
"Если из А следует В и В, то неверно А":
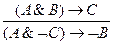 .
.
7. Правило контрапозиции:
"Если из А следует В, то из того, что неверно В, следует, что неверно А":
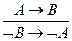 .
.
8. Правило сложной контрапозиции:
"Если из А и В следует С, то из А и С следует B:
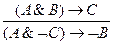 .
.
9. Правило сечения:
"Если из А следует В, а из В и С следует D то из А и С следует D ”:
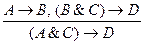 .
.
Приведем без пояснений еще несколько правил умозаключений.
10. Правило импортации (объединения посылок):
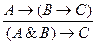 .
.
11. Правило экспортации (разъединения посылок):
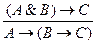 .
.
12. Правила дилемм:
а) 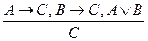 ; б)
; б) 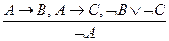 ;
;
в) 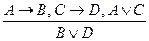 ; г)
; г) 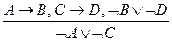 .
.
Примечание. Для построения логических формул, отражающих указанные выше логически правильные рассуждения, следует все посылки соединить связкой "И" (&) и полученную таким образом обобщенную посылку – связкой "если..., то..." (→). Например, правило заключения (Modus Ponens) должно быть представлено логической формулой
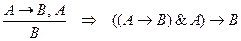 .
.
Схемы логически неправильных рассуждений:
а)  ;
;
б)  ;
;
в) 
и др.
Пример 5. Проверить с помощью таблиц истинности правильность рассуждений представленных:
а) формулой (5) (правило транзитивности)
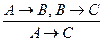 ;
;
б) формулой (6) (правило противоречия)
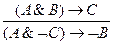 ;
;
в) формулой (7) (правило контрапозиции).
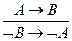 .
.
Решение:
Составим формулы для данных высказываний:
а) 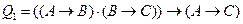 ;
;
б) 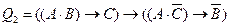 ;
;
в) 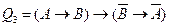 .
.
Составим таблицы истинности для данных составных высказываний. Получим:
а)
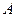
| 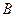
| 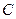
| 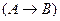
| 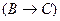
| 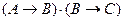
| 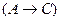
| 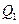
|
б)
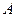
| 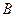
| 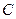
| 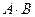
| 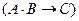
| 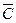
| 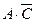
| 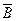
| 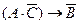
| 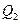
|
в)
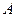
| 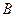
| 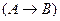
| 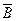
| 
|  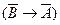
| 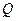
|
Из таблицы видно, что для всех выражений функция принимает значение «истина» при всевозможных значениях элементарных высказываний. Следовательно, данные рассуждения верны.
Пример 6. Проверить с помощью таблиц истинности правильность рассуждений представленных формулами логически неправильных рассуждений:
а)  ;
;
б)  ;
;
в) 
Решение:
Представим данные выражения формулами:
а) 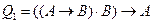 ;
;
б) 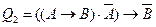 ;
;
в) 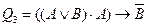 .
.
Таблицы истинности будут иметь вид:
а)
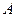
| 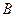
| 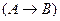
| 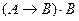
| 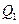
|
б)
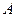
| 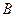
| 
| 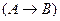
| 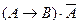
| 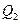
|
в)
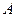
| 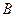
| 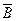
| 
| 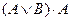
| 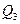
|
Из таблицы видно, что функции принимает значение «ложь» при некоторых значениях элементарных высказываний. Следовательно, данные рассуждение не верны.
Пример 7. Записать логической формулой следующее умозаключение:
«Если фирма приглашает на работу крупного специалиста в области компьютерных технологий, то она считает ее привлекательной и разворачивает работы по изменению технологии производства своего традиционного программного продукта или начинает разработку нового программного продукта. Конкурирующая фирма пригласила на работу крупного специалиста в области компьютерных технологий. Следовательно, она разворачивает работы по изменению технологии производства выпускаемого программного продукта или разработке нового программного продукта».
Уточнить справедливость данного умозаключения.
Решение.
Выделим простые высказывания и введем обозначения:
A – «Фирма приглашает на работу крупного специалиста в области компьютерных технологий»;
B – «Фирма считает данную компьютерную технологию привлекательной»;
C – «Фирма разворачивает работы по изменению технологии производства своего традиционного программного продукта»;
D – «Фирма начинает разработку нового программного продукта».
С учетом принятых обозначений умозаключение примет вид:
«Если A, то B и (C или D). A. Следовательно, C или D.»
Используя логические связки, получим окончательно:
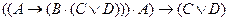 .
.
Для проверки правильности умозаключения восстановим схему рассуждения и сравним ее со схемой правила заключения 1:
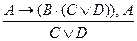 .
.
В соответствии с этим правилом истинно заключение 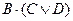 . Конъюнкция двух высказываний B и
. Конъюнкция двух высказываний B и 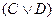 истинна, если истинны оба высказывания. Полагая, что B истинно (что видно из контекста), истинно также
истинна, если истинны оба высказывания. Полагая, что B истинно (что видно из контекста), истинно также 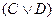 . Таким образом, данное умозаключение верно при истинности B.
. Таким образом, данное умозаключение верно при истинности B.
Пример 8. Следует установить, правильно ли рассуждение:
"Если функция на данном интервале непрерывна и имеет разные знаки на концах, то внутри данного интервала функция обращается в нуль. Функция не обращается в нуль внутри данного интервала, но на концах интервала имеет разные знаки. Следовательно, функция разрывна."
Решение.
Посылки и заключения в данном рассуждении состоят из следующих элементарных высказываний:
А – "Функция непрерывна на данном интервале."
В – "Функция обращается в нуль внутри данного интервала."
С – "Функция имеет разные знаки на концах интервала."
Используя эти обозначения, запишем посылки и заключения в виде формул:
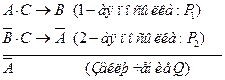
Рассуждение верно, если импликация

тождественно истинна. Для проверки правильности рассуждения построим таблицу истинности:
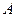
| 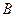
| 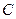
| 
| 
| 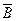
| 
| 
| 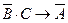
| 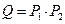
| 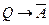
|
Убеждаемся, что рассуждение верно, так как значение результирующей функции всегда истинно.
Пример 9. Следует установить, правильно ли рассуждение:
«Если число делится на 2 и на 3, то оно не делится на 6. Данное число делится на 3. Следовательно, если оно не четное, то оно не делится на 6».
Решение.
Посылки и заключения в данном рассуждении состоят из следующих элементарных высказываний:
А – "Число делится на 2."
В – "Число делится на 3."
С – "Число делится на 6."
Используя эти обозначения, запишем посылки и заключения в виде формул:

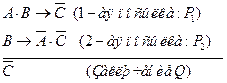
Рассуждение верно, если импликация
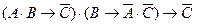
тождественно истинна.
Для проверки правильности рассуждения построим таблицу истинности:
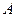
| 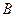
| 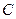
| 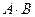
| 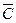
| 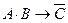
| 
| 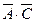
| 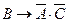
| 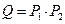
| 
|
Отсюда видно, что рассуждение не верно, так как значение результирующей функции не всегда истинно.
Пример 10. Следует установить, правильно ли рассуждение:
«Если число делится на 2 и на 3, то оно делится на 6. Данное число делится на 3. Следовательно, если оно четное, то оно делится на 6».
Решение.
Посылки и заключения в данном рассуждении состоят из следующих элементарных высказываний:
А – "Число делится на 2."
В – "Число делится на 3."
С – "Число делится на 6."
Используя эти обозначения, запишем посылки и заключения в виде формул:

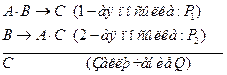
Рассуждение верно, если импликация
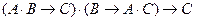
тождественно истинна. Для проверки правильности рассуждения построим таблицу истинности:
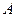
| 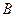
| 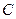
| 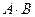
| 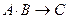
| 
| 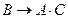
| 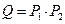
| 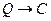
|
Отсюда видно, что рассуждение верно, так как значение результирующей функции всегда истинно.
Date: 2015-09-02; view: 2326; Нарушение авторских прав