Примеры. 3.Рассмотрим . При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0

1. .

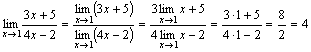2. .

3.Рассмотрим 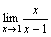. При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как , т.е. есть бесконечно малая функция при x→ 1, то .

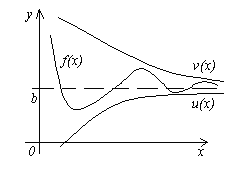Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u (x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если

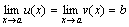, то .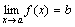

Смысл этой теоремы понятен из рисунка.

Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы 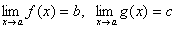, то имеет место неравенство b≥c.

Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5 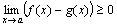, или .

До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что x принимает только значения, меньшие a, то пишут 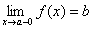и называют bпределом функции f(x) в точке a слева.

Таким образом, число b называется пределом функции y=f(x) при x→a слева, если каково бы ни было положительное число ε, найдется такое число δ (меньшее a), что для всех выполняется неравенство .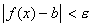

Аналогично, если x→a и принимает значения большие a, то пишут и называют b пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→a справа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех 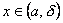выполняется неравенство .

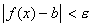Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а.

Date: 2015-09-02; view: 479; Нарушение авторских прав