Мода и медиана, как структурные средние, их использование

Мода (Мо)-значение случайной величины, встречающейся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту. В интервальных рядах распределения с равными интервалами мода вычисляется по формуле: 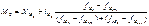, где X(M0) – нижняя граница модального интервала, f(M0),f(M0-1),f(M0+1) – частоты в модальном, предыдущем и следующем за модальным интервалах. Медиана (Ме) – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы. Номер медианы для нечетного объёма вычисляется по формуле: 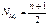. Медиана находит практическое применение в маркетинговой деятельности вследствие особого свойства – сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая. Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения. Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.

25. Понятие и показатели вариации. Вариация – колеблимость, многообразие, изменяемость величины признака у отдельных единиц совокупности. Показатели вариации: средние величины дают обобщающую характеристику совокупности по варьирующим признакам и показывают типичный для данных условий уровень этих признаков. Однако на ряду со средними величинами большое теоретическое и практическое значение имеет изучение отклонений от средних. Поэтому рассматривается ряд показателей, которые характеризуют не только прошлые отклонения (лучшие и худшие параметры) но и совокупность всех отклонений. Абсолютные показатели:1)Размах вариации – R=X(max)-X(min). характеризует пределы изменения варьирующего признака. Достоинства: простота расчёта. Недостаток:зависит от случайных значений признака. Поэтому более надёжным является средний размах вариации, исчисляемый как среднее арифметическое из ряда размахов, полученных в результате обработки серий наблюдений.2)Среднее линейное отклонение – индивидуальное значение признака отклонения от средней в ту или иную сторону и учитывают различия всех единиц изучаемой совокупности.выделяют 2 вида отклонений:1)простое среднее абсолютное отклонение (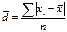), если отдельное значение признака повторяется, то получаем 2)взвешенное среднее абсолютное отклонение(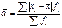). Достоинства: более точно отражает разнородность совокупности. Недостатки: использование абсолютных величин уравнивает положительные и отрицательные значения.3)Дисперсия – средний квадрат отклонений определяемый как среднее из отклонений возведённых в квадрат (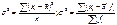). Исчислению дисперсии обычно предшествует подсчёт среднего кВ.отклонения. однако дисперсия имеет самостоятельное значение и отражает самым точным образом однородность совокупности.4) Среднее квадратическое отклонение является общепринятым показателем вариации. При его определении принимается в расчёт все отклонения значения варьирующего признака от средней.достоинства: наиболее точно отражает однородность совокупности. Недостатки: сложен для расчёта, содержит двойные усреднения. Простое и взвешенное: 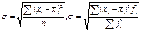.относительные: 1)К-т вариации – относительная мера вариации, позволяющая сравнивать степень изменения признака в вариационных рядах с разным уровнем средних. 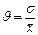.2)К-т ассимиляции (относительный размах)- отражает относительную колеблимость крайних значений признака вокруг средней: 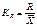.3)Относительное линейное отклонение: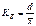

26.

27.

28.

29. Ряд динамики: понятие, элементы и его особенности. Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени. В каждом ряду имеются два основных элемента: время и конкретное значение показателя (уровень ряда). Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Выявление основной тенденции в изменении уровней, именуемой трендом, является одной из главных задач анализа рядов динамики.

30. Средние показатели в рядах динамики. Ряд интерв.с равными интервалами абсолютных и средних величин – средняя арифметическая простая. 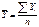.Ряд интервальный с неравными интервалами абсолютных и средних величин 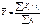делит интервал или делит пер.между уровнями. Ряд интерв.отностительных величин – среднее геометрическое: 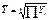. Ряд моментный с равноотстающими моментами времени – средняя хронологическая простая: 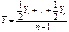. Ряд моментный с неравноотстающими моментами времени – средняя хронологическая взвешенная: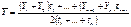

31. Методы сопоставимости рядов динамики. 1)Метод сопоставимости. Прямой пересчёт данных по первичному материалу;2)Метод смыкания рядов. Объединение в один ряд более длинный двух или нескольких рядов, уровни которых исчисляются по разным методологиям, в разных границах. Используется 2 приёма:*смыкание рядов проводится с помощью коэф.соотношения уровней: К(с)=У(н)/У(ст), где У(н),У(ст)- уровни,в которых проводили изменения;*уровень первоначального динамического ряда заменяется базисными темпами роста, причём за базу берётся уровень года,в котором произошли изменения.

32.

33. Основные методы обработки и анализа рядов динамики. Приведение рядов динамики к единому основанию. Назначение приёма: сравнить направление и интенсивность развития нескольких рядов динамики. Сущность приёма: уровни показателей различных явлений или одинаковых, но по разным объектам исследования одного периода в независимости от их абсолютного значения принимаются в качестве базы расчёта. Все другие показатели сравниваются с базой. Полученные темпы роста и прироста сопоставляются между собой и делается вывод об интенсивности явления. Методы выявления тенденции развития: 1)Метод укрупнения интервала (цифры за мелкие периоды внутри крупного экономически обоснованного интервала складываются и рассчитывают среднюю величину). 2)Метод скользящей средней – с первого уровня ряда берётся определённое количество уровней, складываются и рассчитывается среднее. Со второго берётся такое же количество уровней, складывается и берётся среднее. 3)Метод аналитического выравнивания. Основное содержание этого метода в том, что общая тенденция развития рассчитывается как функция времени.

34.

35. Статистические индексы: понятие, виды и роль в изучении социально-экономических явлений. Индексом в статистике называют относительный показатель, характеризующий изменение величины какого-либо явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов) во времени, пространстве или по сравнению с любым эталоном (нормативом, планом, прогнозом). Когда рассматривается сопоставление уровней изучаемого явления во времени, то говорят об индексах динамики, в пространстве – о территориальных индексах, при сопоставлении с уровнем, например, договорных обязательств – об индексах выполнения обязательств. Основным элементом индексного отношения является индексируемая величина- значение признака статистической совокупности, изменение которой является объектом изучения. С помощью индексов решаются следующие основные задачи:1)позволяют измерять изменение сложных явлений;2)можно определить влияние отдельных факторов на изменение динамики сложного явления (влияние изменения уровня цен и изменения количества проданных товаров на объём товарооборота);3)они являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами, планами, прогнозами. Индексы классифицируются:*по содержанию изучаемых объектов:(количественные и индексы качественных показателей);*по степени охвата элементов совокупности:(индивидуальные и общие);*по методам расчёта общих индексов:(агрегатные и средние).

36. Индивидуальные и общие индексы. Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления (например, изменение объёма выпуска телевизоров определённой марки, рост или падение цен на акции в каком-либо акционерном обществе). Индивидуальные индексы относятся к одному элементу(явлению) и не требуют суммирования данных. Они представляют собой относительные величины динамики, выполнения обязательств, сравнения. Выбор базы сравнения определяется целью исследования. Общий индекс отражает изменение всех элементов сложного явления. При этом под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (физический объём продукции, включающий разноимённые товары, цены на разные группы продуктов). Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми или субиндексами (например, индексы физического объема продукции по отдельным отраслям промышленности).

37. Агрегатные индексы. Порядок построения индексов качественных показателей. Любые общие индексы могут быть построены двумя способами: как агрегатные и как средние из индивидуальных. Последние в свою очередь делятся на средние арифметические и средние гармонические. Агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного состава и индексы постоянного (фиксированного) состава. В индексах переменного состава сопоставляются показатели, рассчитанные на базе изменяющихся структур явлений, в индексах постоянного состава – на базе неизменной структуры явлений.Агрегатный индекс является основной и наиболее распространенной формой индекса, его числитель и знаменатель представляют собой – «агрегат» (суммируемый) непосредственно несоизмеримых и не поддающихся суммированию элементов – сумму произведения двух величин, одна и которых меняется, а другая остаётся неизменной в числителе и знаменателе. Агрегатная форма индексов рассчитывается путём сопоставления итогов сложения показателей в отчётном и базисном периодах при помощи соизмерителя. Индекс качественного показателя рассматриваются на примере построения общего индекса цен;1)фор-ла агрегатного индеса: 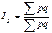;2)индексир.величиной является цена- качественный показатель 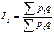;3)фиксированная величина физич.объём продукции-фиксированный показатель.Правило:В индексах качественного показателя фиксированная величина является весами и их следует брать на отчётном уровне.;4)Формула индекса: 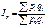.абсолютное изменение стоимости продукции за счёт изменения цены: 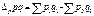. Общее изменение стоимости продукции в отчётном периоде по сравнению с базисным можно рассчитать с помощью общего индекса стоимости: .

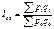38. Агрегатные индексы. Порядок построения индексов объёмных показателей.

Любые общие индексы могут быть построены двумя способами: как агрегатные и как средние из индивидуальных. Последние в свою очередь делятся на средние арифметические и средние гармонические. Агрегатный индекс является основной и наиболее распространенной формой индекса, его числитель и знаменатель представляют собой – «агрегат» (суммируемый) непосредственно несоизмеримых и не поддающихся суммированию элементов – сумму произведения двух величин, одна и которых меняется, а другая остаётся неизменной в числителе и знаменателе. Агрегатная форма индексов рассчитывается путём сопоставления итогов сложения показателей в отчётном и базисном периодах при помощи соизмерителя. Индексы количественных показателей – индексы физического объёма промышленной и сельскохозяйственной продукции, физического объёма розничного товарооборота, национального дохода, потребления продаж иностранной валюты. Все индексируемые показатели этих индексов являются объёмными, поскольку они характеризуют общий, суммарный размер (объём) того или иного явления и выражаются абсолютными величинами. При расчёте таких индексов количества оцениваются в одинаковых, сопоставимых ценах. Индекс физического объёма продукции: сложность при построении этого индекса заключается в том, что объёмы разных видов продукции и товаров в натуральном выражении несоизмеримы и непосредственно суммироваться не могут. Причиной несоизмеримости является неоднородность. Отношение стоимости продукции текущего периода в текущих ценах 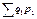к стоимости продукции базисного периода в базисных ценах 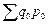представляет собой агрегатный индекс стоимости продукции или товарооборота: 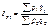. Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчётного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции. Разность числителя и знаменателя показывает на сколько денежных единиц увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. Для того, чтобы индекс охарактеризовал изменение только одного фактора, нужно устранить в формуле влияние другого фактора, зафиксировав его как в числителе, так и в знаменателе на уровне одного и того же периода. Так, если продукцию сравниваемых периодов оценивать по одним и тем же, например базисным ценам (р0), то такой индекс отразит изменение только одного фактора – индексируемого показателя ку и будет представлять собой агрегатный индекс физического объема продукции: 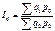. индекс физического объёма продукции показывает, во сколько раз увеличится (уменьшится) физический объём продукции или сколько процентов составляет его рост (снижение) в отчётном периоде по сравнению с базисным периодом. Индекс физического объёма в форме среднего арифметического индекса физического объёма продукции: 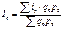. Индекс физ.объёма в форме среднего гармонического взвешенного индекса физического объёма продукции, где весами служит стоимость продукции отчётного периода в базисных ценах: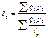

39. Средние индексы: сущность и порядок расчёта. К исчислению средневзвешенных индексов прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если неизвестны количества произведенных отдельных видов продукции в натуральных измерителях, но известны индивидуальные индексы и стоимость продукции базисного периода, можно определить средний арифметический индекс физического объёма продукции. Исходной базой построения средневзвешенного индекса физического объёма продукции служит его агрегатная форма: 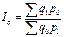. из имеющихся данных непосредственно можно только получить знаменатель этой формулы. Для нахождения числителя используем формулу индивидуального индекса объёма продукции: 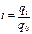из которой следует, что 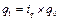.подставив,получаем общий индекс физического объёма в форме среднего арифметического индекса физического объёма продукции, 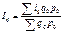.также можно получить общий индекс физического объёма в форме среднего гармонического взвешенного индекса физического объёма продукции, где весами служит стоимость продукции отчётного периода в базисных (или сопоставимых ценах): .

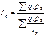40.

Date: 2015-08-22; view: 977; Нарушение авторских прав