
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Увеличение скорости передачи данных
|
|
Для увеличения скорости передачи в сетях радиодоступа используют:
- агрегацию полос,
- пространственное мультиплексирование.
Агрегация (объединение) частотных полос является основным способом увеличения скорости передачи данных. При агрегации полос одновременно с передачей в базовой полосе частот появляется возможность вести передачу еще в одной или нескольких полосах. При этом в каждой новой полосе формируют свой индивидуальный сигнал Это означает, что передают несколько независимых сигналов, которые могут принимать как один терминал, так и разные терминалы. Оператор может выбирать полосы из одного диапазона (подряд или с промежутками) или из разных диапазонов. На рис. 5.1 показаны варианты агрегации полос в сетях LTE.
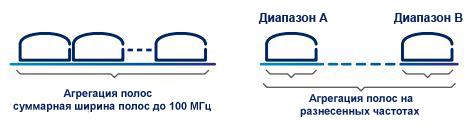
Рис.5.1. Варианты выделения полос при агрегации
Для приема сигналов с агрегацией полос требуется использовать многоканальные приемники.
MIMO (Multiple Input – Multiple Output) ‒ многоантенные технологии, используемые для решения двух задач:
- повышения качества связи за счет пространственного временного/частотного кодирования и (или) формирования лучей (beamforming),
- увеличения скорости передачи при использовании пространственного мультиплексирования.
В любом варианте MIMO речь идет об одновременной передаче в одном физическом канале нескольких сообщений. Для реализации MIMO используют многоантенные системы: на передающей стороне имеется M передающих антенн, а на приемной стороне N приемных. Эту структуру поясняет рис. 5.2.
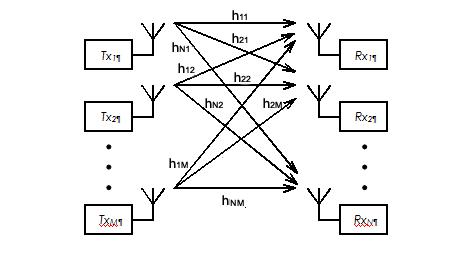
Рис.5.2. Модель канала с М передающими и N приемными антеннами
Математическая модель, описывающая систему (рис.4.2), представляет собой векторное уравнение
r = H × s + n (5.1)
где r и s - вектора принятых и переданных сигналов, а n – вектор помех на входе приемников.
Коэффициенты передач между различными передающими и приемными антеннами определяет матрица H:
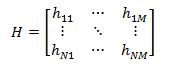 (5.2)
(5.2)
Рассмотрим простую задачу пространственного мультиплексирования, когда на передающей стороне (eNB) 2 антенны и на приемной (UE) – тоже 2 приемные антенны. Поток символов s1 идет через передающую антенну Tx1, поток символов s2 через передающую антенну Tx2. Каждая приемная антенна (Rx1 и Rx2) принимает взвешенную сумму сигналов s1 и s2. Векторное уравнение (5.1) будет следующим:
r1 = h11 s1 + h12 s2 + n1
r2 = h21 s1 + h22 s2 + n2 (5.3)
Задача приемника абонентского терминала состоит в том, чтобы получить из принятых сигналов s1 и s2. Сигналы r1 и r2 принимает приемник мобильного терминала. Для решения системы линейных уравнений (5.3) необходимо знать коэффициенты передач hij. Для этого каждая передающая антенна транслирует специальные заранее известные опорные сигналы, принимая которые приемник определяет массив коэффициентов передачи hij. В результате получаем:
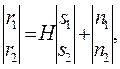 где
где 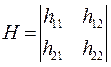
Вычислив обратную матрицу H-1, получаем
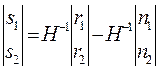 (5.4)
(5.4)
Система (5.4) представляет собой алгоритм работы ZF-приемника. Разделение приемником сигналов s1 и s2 возможно, если существует обратная матрица H-1, то-есть, коэффициенты передачи hij между собой не коррелированы.
При использовании пространственного мультиплексирования существенно усложняется построение приемников. Каждый независимый поток данных создает помехи другим потокам. Поэтому пространственное мультиплексирование реализуют в “хороших” каналах, с высоким отношением сигнал/помеха. Для разделения потоков в приемнике необходимо, чтобы число приемных антенн N было не меньше числа передаваемых потоков данных. Если принять, что каждый поток идет через одну передающую антенну, то в соответствии с рис.5.2 N 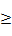 M. Теория и практика показывают, что с увеличением числа приемных антенн (например, при N=4 и М=2 в сравнении с вариантом N=2 и М=2) коэффициент ошибок снижается.
M. Теория и практика показывают, что с увеличением числа приемных антенн (например, при N=4 и М=2 в сравнении с вариантом N=2 и М=2) коэффициент ошибок снижается.
Опишем различные алгоритмы обработки сигналов в приемнике при пространственном мультиплексировании.
Алгоритм максимального правдоподобия. Приемник максимального правдоподобия выполняет векторное декодирование и является оптимальным в смысле минимизации вероятности ошибки. В приемнике производят перебор всех возможных вариантов переданного вектора s. При равной вероятности передачи любых вариантов s искомым сигналом считают 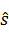 , минимизирующий оценку:
, минимизирующий оценку:
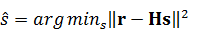 (5.5)
(5.5)
Прямая реализация алгоритма при двух независимых потоках и модуляции 16-КАМ требует перебора 162 возможных состояний сигнала, при 4 потоках ‒ 164, а при модуляции 64-КАМ 644 состояний. Просмотр такого числа вариантов пока практически нереализуем, хотя методы сферического декодирования, требующие дополнительного совместного исследования матрицы Н и помех, позволяют существенно уменьшить зону поиска.
Линейные алгоритмы.
Линейные алгоритмы основаны на решении системы М линейных уравнений, получаемых путем псевдообращения матрицы коэффициентов Н (5.2). Этот алгоритм принято называть ZF (Zero-Forcing). Если матрица Н квадратная, то-есть, число независимых потоков данных М равно числу приемных антенн N, то вектор переданных сигналов s можно определить, умножив левую и правую части (5.1) на обратную матрицу H-1 и решив следующую систему уравнений:
s = H-1 × r – H-1 × n (5.6)
Если число приемных антенн N больше числа принимаемых потоков данных М, то матрица Н становится прямоугольной размерностью N×М (НNM). В этом случае выполняют псевдообращение матрицы НMP по алгоритму Мура-Пенроуза, где используют матрицу НН, эрмитово-сопряженную с матрицей Н. Матрицу НН получают, транспонируя матрицу Н и заменяя все элементы hij на их комплексно-сопряженные значения. Оператор
 (5.7)
(5.7)
имеет размерность М×N. Заменив в (4.6) H-1 на НMP, получаем
s = НMP × r – НMP × n (5.8)
Оба варианта ZF-приемника (5.6) и (5.8) отличаются вычислительной простотой, но дают существенно худший результат в сравнении с алгоритмом максимального правдоподобия, поскольку после умножения НMP × n усиливается влияние помех.
С целью улучшения приема используют модифицированный ZF-алгоритм, получивший название MMSE (Minimum Mean Square Error). В MMSE-приемнике оператор НMP заменен оператором WMMSE:
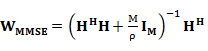 (5.9)
(5.9)
где  - соотношение сигнал/помеха, а
- соотношение сигнал/помеха, а 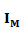 – единичная матрица размерности M.
– единичная матрица размерности M.
Нелинейные алгоритмы.
Нелинейные алгоритмы приемников сигналов с пространственным мультиплексированием дают лучшие результаты, чем линейные, но требуют значительно бόльшего объема вычислений. Одним из наиболее известных нелинейных алгоритмов является Vertical-Bell Labs Layered Space Time Architecture или V-BLAST. Алгоритм работы V-BLAST включает в себя как линейные, так и нелинейные операции. Он основан на QR-разложении канальной матрицы HNM с последующим определением и исключением отдельных принятых символов. Матрицу HNM представляют в виде произведения
НNM = QNM RMM (5.10)
где QNM –унитарная матрица, удовлетворяющая условию:
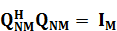 ,
,
а RMM – диагональная матрица вида
 (5.11)
(5.11)
Далее преобразовываем уравнение (5.1), умножая его левую и правую части на 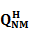 , к виду
, к виду
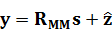 , (5.12)
, (5.12)
где вектор  , а вектор
, а вектор 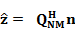 . Отметим, что вследствие унитарности матрицы
. Отметим, что вследствие унитарности матрицы 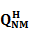 мощность помех не возрастает. В результате получаем систему уравнений
мощность помех не возрастает. В результате получаем систему уравнений
 (5.13)
(5.13)
которую решаем, находя компоненты вектора s, начиная с последнего sM. Нелинейность алгоритма состоит в том, что при последовательном решении системы (5.13) рассчитанные значения символов sM, sM-1 …заменяют точными значениями используемого дискретного множества сигналов.
Результаты компьютерного моделирования работы детектора V-BLAST в зависимости от отношения сигнал/суммарная помеха (SNR) приведены на рис.5.3. Смоделирована передача 2 потоков данных с модуляцией 16-КАМ при приеме на 2 антенны.
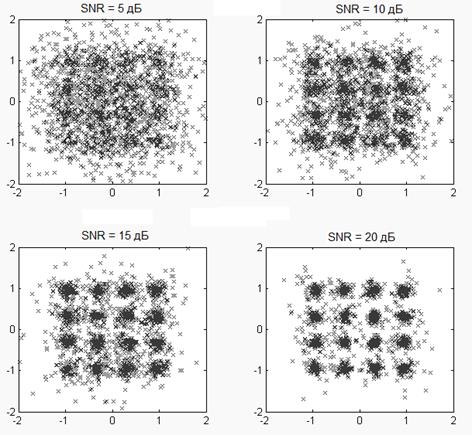
Рис. 5.3. Прием сигналов при пространственном мультиплексировании
Date: 2015-09-02; view: 671; Нарушение авторских прав