
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Наращение по учетной ставке
|
|
Пример
Клиент поместил в банк вклад в сумме 35 тыс. руб. под 15 % годовых.
Какова будет суммарная величина процентных денег, если:
а) проценты будут начисляться один раз в конце года;
б) проценты будут начисляться ежемесячно?
В первом случае FV – PV = 35* 0,15* 1 год = 5,25 тыс. руб.
Во втором случае FV – PV = 35* 1/12* 0,15 = 437,5 руб.
Т.е. во втором случае суммарный годовой доход клиента в виде начисленных процентов составит те же 437,5* 12 = 5,25 тыс. руб.
При определении продолжительности финансовой операции принято день выдачи и день погашения ссуды считать одним днем. В зависимости от того, чему принимается равной продолжительность периода сделки (год, квартал, месяц), размер промежуточной процентной ставки может быть различным. Возможны следующие варианты:
1) точный процент (exact interest), определяемый исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);
2) обыкновенный процент (ordinary interest), определяемый исходя из приближенного числа дней в году, квартале, месяце (соответственно, 360, 90, 30).
При определении продолжительности периода, на который выдана ссуда, также возможны два варианта:
1) в расчет принимается точное число дней, на которое выдана ссуда;
2) в расчет принимается приближенное число дней, не которое выдана ссуда (исходя из продолжительности месяца 30 дней).
Исходя из сказанного, расчет может выполняться одним из трех способов:
1) Точный процент с точным числом дней. Этот вариант дает самые точные результаты (Великобритания, США). Обозначение 365/365, ACT/ACT.
2) Обыкновенный процент с точным числом дней. Этот метод иногда называют банковским (Banker’s Rule), распространен в ссудных операциях коммерческих банков, в частности во Франции, Бельгии. Этот вариант дает несколько больший результат, чем применение точных процентов. При числе дней ссуды, превышающем 360, данный способ приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой. Например, если t=364, то n=364/360=1,011. Обычно это условие финансовой сделки обозначается как 365/360, ACT/360.
3) Обыкновенный процент с приближенным числом дней. Такой метод применяется тогда, когда не требуется большой точности, например при промежуточных расчетах. Он принят в коммерческих банках Германии. Обозначение в условиях финансовой сделки 360/360, или немецкая практика;
Вариант с точными процентами и приближенным числом дней ссуды лишен смысла и не применяется.
Величина эффекта от выбора того или иного способа зависит от размеров суммы, фигурирующей в процессе финансовой операции.
Пример. Банк выдал кредит 20.01. в размере 500 тыс. руб. Срок возврата кредита 05.10. Процентная ставка установлена в размере 15% годовых. Год не високосный.
Точное число дней (по таблице) = 278 - 20 = 258 дня.
Приближенное число дней = 12 дней января + 30 дней февраля + 30 дней марта + 30 дней апреля + 30 дней мая + 30 дней июня + 30 дней июля + 30 дней августа + 30 дней сентября + 5 дней октября – 1 день = 256 дней.
Ø точный процент и точное число дней
 тыс. руб.
тыс. руб.
Ø обыкновенный процент и точное число дней
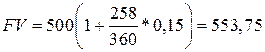 тыс. руб.
тыс. руб.
Ø обыкновенный процент и приближенное число дней
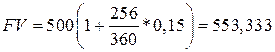 тыс. руб.
тыс. руб.
Между величинами процентного дохода, рассчитанными с использованием различной временной базы, при равной продолжительности ссуды существуют следующие соотношения:

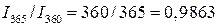
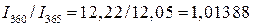
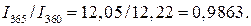
Эти соотношения могут быть использованы при определении эквивалентных процентных ставок, то есть ставок, приносящих одинаковые процентные доходы при различных временных базах, но равных первоначальных капиталах:
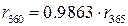
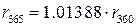
В мировой практике при расчете процента используют и другие величины.
Пусть 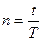 . Тогда в формуле процентных денег
. Тогда в формуле процентных денег 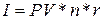 можно записать
можно записать 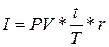 . Поделив числитель и знаменатель дроби правой части равенства на r, получим:
. Поделив числитель и знаменатель дроби правой части равенства на r, получим:
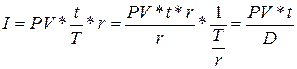 , где
, где 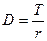 .
.
В этих формулах –  т.н. процентное число;
т.н. процентное число;
– 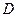 процентный ключ или дивизор.
процентный ключ или дивизор.
Естественно, что при одной и той же ставке  , но при различных значениях
, но при различных значениях 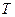 (360 или 365 дней) будет разным и дивизор.
(360 или 365 дней) будет разным и дивизор.
Дивизор численно равен такому количеству денежных единиц, с которого при ставке процента 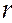 получается 1 денежная единица в день.
получается 1 денежная единица в день.
Если PV = 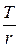 руб. (при t=T), то I =
руб. (при t=T), то I = 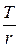 *
* 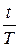 *r = t (руб.в день).
*r = t (руб.в день).
Пример. Вычислить процент с капитала в 2,4 млн. руб., отданного в долг по ставке 16% годовых на срок с 05.03. по 21.09. того же года, если расчет ведется способом 365/365.
t = 264 –64 = 200 дней.
D = 365/0,16 = 2281,25
I = 2,4*200/2281,25 = 0,210411 млн. руб.
Проверим: FV = 2281.25*(1 + 200/365*0,16) = 2481.25 руб.
Доход от операции 2481.25 – 2281.25 = 200 руб. за 200 дней или 1 руб. дохода за день финансовой операции (что и требовалось доказать).
Переменные ставки и реинвестирование.
Финансовое соглашение может предусматривать не только постоянную процентную ставку за весь период, но и устанавливать изменяющуюся во времени, т.е. переменную ставку.
Это, как правило, вызывается наличием инфляции, что вынуждает участников финансовой операции периодически варьировать величиной процентной ставки.
В частности, в соглашении м.б. оговорена т.н. плавающая процентная ставка, когда фиксируется не сама ставка, а изменяющаяся во времени ее база и маржа (или величина надбавки к базе).
Величина маржи м.б. на протяжении срока сделки как постоянной, так и переменной.
Пусть на период времени 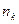 установлена процентная ставка
установлена процентная ставка  . Тогда приращение капитала за этот период будет равняться величине
. Тогда приращение капитала за этот период будет равняться величине
 . Если таких периодов будет
. Если таких периодов будет  (т.е.
(т.е.  ), то наращенная сумма за время
), то наращенная сумма за время  будет определяться по формуле:
будет определяться по формуле:
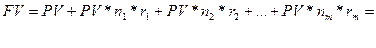
 .
.
Возможен и другой подход к решению подобной задачи, когда величина наращенной стоимости определяется с помощью средней процентной ставки за весь период времени финансовой операции.
В этом случае:
 , а
, а 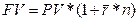
Пример. Вкладчик поместил в банк 10 тыс. руб. на следующих условиях: в первый год процентная ставка равна 16% годовых, каждые последующие полгода ставка повышается на 1.5%. Найти наращенную сумму за три года, если проценты начисляются только на первоначальную сумму вклада.
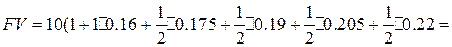 15,55 тыс. руб.
15,55 тыс. руб.
или
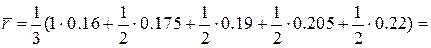 0,185 (18.5%)
0,185 (18.5%)
FV=10 000 (1+18.5*3)=15 000 (руб.)
Финансовые контракты могут предусматривать условия, согласно которым за период времени 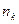 установлена процентная ставка
установлена процентная ставка  , но при изменении (или без изменения) ставки наращения к этому моменту времени полученная сумма вкладывается вновь под новый простой процент.
, но при изменении (или без изменения) ставки наращения к этому моменту времени полученная сумма вкладывается вновь под новый простой процент.
Такая финансовая операция называется реинвестированием (капитализацией) полученных на каждом этапе наращения средств. Согласно этому условию, через время 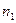 наращенная сумма составит величину
наращенная сумма составит величину 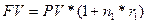 , после чего она будет переоформлена на следующий срок
, после чего она будет переоформлена на следующий срок  . Через время
. Через время  наращенная сумма станет равной величине:
наращенная сумма станет равной величине: 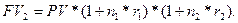 .
.
Рассуждая аналогичным образом, получим формулу для нахождения наращенной суммы за время  при реинвестировании:
при реинвестировании:
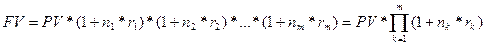 .
.
В этой формуле множитель 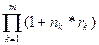 представляет собой, по существу, индекс роста суммы
представляет собой, по существу, индекс роста суммы 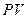 за время
за время 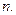
Пример. Вкладчик поместил в банк 15 тыс. руб. на следующих условиях: в первый год процентная ставка составляет 20% годовых, а в каждые последующие полгода ставка повышается на 3%. Найти наращенную за 2 года сумму вклада, если проценты начисляются с одновременной капитализацией процентного дохода.
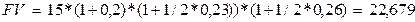 тыс. руб.
тыс. руб.
Дисконтирование по схеме простых процентов.
При заключении финансовых соглашений часто приходится решать задачу, обратную задаче нахождения наращенной суммы.
Например, по заданной сумме FV, которую предполагают получить (или уплатить) за время 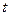 , требуется определить величину капитала PV, который необходимо инвестировать в данный момент, чтобы через время
, требуется определить величину капитала PV, который необходимо инвестировать в данный момент, чтобы через время 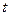 при постоянной процентной ставке получить сумму FV. Аналогичная задача возникает и в том случае, если проценты удерживаются непосредственно при выдаче ссуды. В этих случаях говорят, что сумма FV дисконтируется или учитывается, а сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты – дисконтом.
при постоянной процентной ставке получить сумму FV. Аналогичная задача возникает и в том случае, если проценты удерживаются непосредственно при выдаче ссуды. В этих случаях говорят, что сумма FV дисконтируется или учитывается, а сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты – дисконтом.
Термин дисконтирование употребляется и в более широком смысле – как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени. Такой прием часто называют приведением стоимостного показателя к некоторому, обычно начальному, моменту времени.
Величину PV, найденную с помощью дисконтирования называют современной величиной, а иногда, в зависимости от контекста текущей или капитализированной стоимостью.
Современная величина суммы денег является одним из важнейших понятий в количественном анализе финансовых операций. В большинстве случаев именно с помощью дисконтирования, а не наращения учитывается такой фактор как время.
В зависимости от вида процентной ставки применяют два вида дисконтирования – математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором случае – учетная ставка.
Математическое дисконтирование представляет собой решение задачи, обратной наращению первоначальной суммы ссуды. Задача в этом случае формулируется так: какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму FV при условии, что на долг начисляются проценты по ставке r?
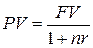
Разность FV-PV в данном случае можно рассматривать не только как проценты, начисленные на PV, но и как дисконт с суммы FV. Обозначим его символом D.
Пример. Через 180 дней после подписания договора должник уплатит 310 тыс. руб. Кредит выдан под 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?
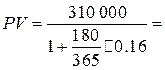 287 328,59 тыс. руб.
287 328,59 тыс. руб.
Банковский учет (учет векселей).
Дисконтирование часто применяется при операциях по так называемому учету векселей банком или другими финансовыми учреждениями.
Рассмотрим наиболее распространенную ситуацию, когда владелец векселя на сумму 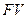 (сумма к погашению, номинал) предлагает банку раньше срока оплаты купить у него вексель.
(сумма к погашению, номинал) предлагает банку раньше срока оплаты купить у него вексель.
Такая покупка векселя у владельца до наступления срока оплаты по цене, меньшей той суммы, которая должна быть выплачена по векселю в конце срока (меньше номинала), называется дисконтированием (учетом) векселя. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя.
Таким образом, векселедержателю досрочно выплачивается обозначенная в векселе сумма за вычетом определенных процентов, удерживаемых банком в свою пользу и называемых дисконтом. В данном случае дисконт представляет собой проценты, начисленные за время 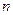 от дня дисконтирования до дня погашения векселя. Если банком объявлена ставка дисконтирования (учетная ставка) d, то величина дисконта составит D=FV*n*d, а владелец векселя получит на руки сумму PV=FV-FV*n*d=FV(1-n*d)
от дня дисконтирования до дня погашения векселя. Если банком объявлена ставка дисконтирования (учетная ставка) d, то величина дисконта составит D=FV*n*d, а владелец векселя получит на руки сумму PV=FV-FV*n*d=FV(1-n*d)
Если продолжительность финансовой операции по учету векселя меньше года, то формула для определения дисконтированной стоимости векселя имеет следующий вид:
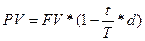 .
.
Из приведенных формул видно, что величина дисконта пропорциональна времени и ставке дисконтирования. Естественно, что чем выше значение ставки дисконтирования, тем большую сумму удержит банк в свою пользу. Учет векселя чаще всего осуществляется способом 365/360.
Пример. Векселедержатель предъявил 13.09 для учета вексель на сумму 50 тыс. руб. со сроком погашения 28.09. Банк согласился учесть вексель по учетной ставке 30% годовых. Определить сумму, которую векселедержатель получит от банка.
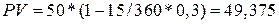 тыс. руб.
тыс. руб.
Разность между номинальной и дисконтированной величиной векселя представляет собой комиссионные, удерживаемые банком в свою пользу, в данном случае 625 руб.
В финансовых сделках возможны ситуации, когда вексель предусматривает начисление простых процентов на сумму по обязательству по процентной ставке. В этом случае при учете векселя исходят из наращенной к сроку погашения векселя суммы.
Пример. Вексель на сумму 10 тыс. руб. был выдан на 150 дней, при этом предусматривалось начисление на указанную сумму простых процентов по ставке 16% годовых способом АСТ/АСТ. За 80 дней до срока погашения вексель вексель был учтен банком по учетной ставке 15% годовых способом 365/360. Определить дисконт, полученный банком.
Сумма, которая должна быть выплачена предъявителю векселя при его погашении:  тыс. руб.
тыс. руб.
Комиссионные банка: 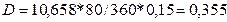 тыс. руб.
тыс. руб.
Наращение по учетной ставке.
В финансовых операциях иногда рассматриваются задачи, обратные банковскому дисконтированию. Пусть от учета капитала 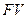 по учетной ставке
по учетной ставке 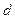 за время
за время 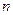 была получена сумма
была получена сумма 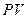 . Требуется определить величину
. Требуется определить величину 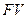 . Задачи такого типа возникают, например, при определении суммы, которую надо написать на векселе, если задана текущая величина долга.
. Задачи такого типа возникают, например, при определении суммы, которую надо написать на векселе, если задана текущая величина долга.
Пример. За вексель, учтенный за полтора года до срока по дисконтной ставке 8%, заплачено 2,2 тыс. руб. Определить номинальную величину векселя.
 тыс. руб.
тыс. руб.
Приращение капитала на основе простой учетной ставки вычисляется о формуле:
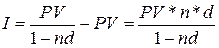 .
.
Из приведенной формулы видно, что приращение капитала на основе простой учетной ставки не пропорционально ни времени финансовой операции, ни ставке дисконтирования.
В данном случае величина 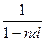 является множителем наращения. Этот множитель равен индексу роста капитала
является множителем наращения. Этот множитель равен индексу роста капитала 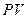 за время финансовой операции и является обратной величиной коэффициента дисконтирования.
за время финансовой операции и является обратной величиной коэффициента дисконтирования.
При наращении капитала на основе простой процентной ставки капитал ежегодно увеличивается на одну и ту же величину 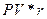 . Если же наращение осуществляется на основе простой учетной ставки, то величина начисляемых процентов с каждым годом увеличивается.
. Если же наращение осуществляется на основе простой учетной ставки, то величина начисляемых процентов с каждым годом увеличивается.
Пользуясь формулой  , запишем приращение капитала
, запишем приращение капитала 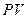 за каждый год финансовой операции.
за каждый год финансовой операции.
За первый год исходный капитал увеличится на величину:
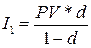 .
.
За два года капитал увеличится на  , и, следовательно, его приращение за второй год составит:
, и, следовательно, его приращение за второй год составит:
 .
.
За три года исходный капитал увеличится на величину  и, следовательно, его приращение за третий год составит:
и, следовательно, его приращение за третий год составит:
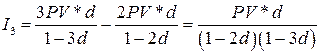 и т.д.
и т.д.
Следовательно, за  год
год 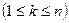 капитал увеличится на величину:
капитал увеличится на величину:
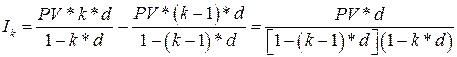 .
.
Пример. На капитал в 3 млн. руб. в течение 5 лет осуществляется начисление простыми процентами по учетной ставке 12%. Найти наращение первоначального капитала за каждый год и общую наращенную сумму.
Общая наращенная сумма составит 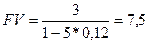 млн. руб.
млн. руб.
Приращение исходного капитала за 5 лет 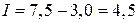 млн. руб.
млн. руб.
Приращение капитала за каждый год финансовой операции:
 млн. руб.
млн. руб.
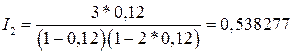 млн. руб.
млн. руб.
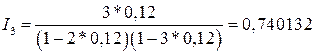 млн. руб.
млн. руб.
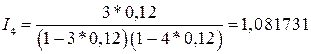 млн. руб.
млн. руб. 
 млн.руб.
млн.руб.
Просуммировав приращение капитала за каждый год финансовой операции, получим 4,5 млн. руб.
Для рассмотренного примера найдем соотношение между годовой процентной и учетной ставками, которые обеспечивают через период времени 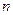 получение одной и той же наращенной величины
получение одной и той же наращенной величины 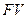 из начального капитала
из начального капитала 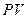 .
.
Поскольку  и
и 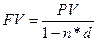 , то из равенства
, то из равенства
 путем несложных преобразований получим
путем несложных преобразований получим 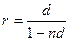 и
и 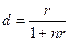 . В соответствии с этой формулой, процентная ставка, эквивалентная учетной ставке 12% годовых, составит 0,3 или 30%.
. В соответствии с этой формулой, процентная ставка, эквивалентная учетной ставке 12% годовых, составит 0,3 или 30%.
Значит, наращенная сумма составит:
 млн. руб
млн. руб
.
Видим, что приращение составляет те же 4,5 млн. руб. Однако, ежегодное наращение будет равномерным и составлять 0,9 млн. руб. в год.
Определение срока ссуды и величины процентной ставки.
При заключении финансовых договоров часто приходится решать не только задачи определения наращенной суммы или приведенной стоимости. Кроме этого может возникнуть необходимость в нахождении других параметров, а именно, процентных и учетных ставок или срока финансовой операции.
Если заданы начальный капитал, наращенная сумма и процентная или учетная ставка, то срок ссуды находится по следующей формулам:
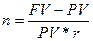 или
или 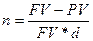 .
.
В этих формулах срок финансовой операции измеряется в годах. Если возникает необходимость определения срока финансовой операции в других единицах времени (например, в днях, что часто бывает при использовании схемы простых процентов), то эти формулы примут соответственно вид:
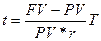 и
и 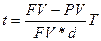 .
.
где 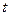 - срок ссуды в днях;
- срок ссуды в днях;
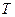 - количество дней в году.
- количество дней в году.
Пример. Необходимо определить время, за которое первоначальный капитал в 3 тыс. руб. при простых процентах возрастет до 3,6 тыс. руб., если используется:
а) процентная ставка 10% годовых;
б) учетная ставка 15% годовых.
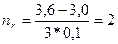 года и
года и 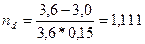 года или примерно 1 год и 40 дней.
года или примерно 1 год и 40 дней.
Пример. На какой срок клиент может взять кредит в размере 4 тыс. руб. под простые проценты с условием, чтобы величина возвращаемой суммы не превышала 4,2 тыс. руб., если процентная ставка равна 12% годовых и в расчет принимаются точные проценты с точным числом дней?
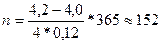 дня.
дня.
При оценке эффективности различных финансовых операций зачастую необходимо определить размер необходимой процентной или учетной ставки. Это необходимо в тех случаях, когда при заключении финансового соглашения ставки не заданы в явном виде. В этом случае используются следующие формулы:
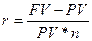 или
или 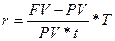 ;
;
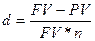 или
или  .
.
Пример. В финансовом договоре клиента с банком предусмотрено погашение долга в размере 5,3 тыс. руб. через 90 дней при взятом кредите в 5 тыс. руб. Определить доходность такой сделки для банка в виде годовых процентной и учетной ставок. В данной финансовой операции банком используются обыкновенные проценты.
 или
или 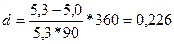
Пример. Вкладчик хочет положить на депозит 8 тыс. руб. и за 10 месяцев накопить не менее 9 тыс. руб. Определить требуемую простую процентную ставку, на основании которой вкладчик должен выбрать банк для размещения своих средств, если в расчете применяются обыкновенные проценты и приближенное число дней.



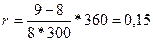 или 15% годовых.
или 15% годовых.
Тема 3
Date: 2015-09-02; view: 2676; Нарушение авторских прав