Генетическая структура популяций

Частоты аллелей и генотипов. Генетическую структуру популяции мы можем описать, определив частоты генотипов в ее генофонде. Для этого нам нет необходимости обследовать всех особей этой популяции. Биологи, как правило, анализируют выборку особей из популяции. Чем больше эта выборка, тем точнее она представляет реальное соотношение частот генотипов в популяции. В качестве материала используются полевые наблюдения, данные лабораторных анализов полевых сборов или музейных экземпляров и даже архивные данные.

Примером может служить наблюдаемое в популяциях лисиц, населяющих Камчатку, Чукотку, Аляску и прилежащие острова, разнообразие по окраске меха, которое контролируется двумя аллелями гена В. Чернобурые лисицы имеют генотип ВВ, красные генотип bb, а у гетерозигот Bb наблюдается промежуточный тип окраски. Их называют сиводушками. Генетический контроль этого признака был расшифрован в ХХ веке, а сбор данных по частотам отдельных окрасочных фенотипов в локальных популяциях проводился задолго до того, как возникла сама наука генетика. Меха лисиц всегда были ценным товаром, и цена меха сильно зависела от окраски. Самыми дорогими считались чернобурые ВВ, сиводушки Bb стоили дешевле и самыми дешевыми были красные bb. Поэтому во всех налоговых книгах и бухгалтерских ведомостях, начиная с XVII века, эти три типа мехов учитывались отдельно. Используя этот уникальный архивный материал, мы можем оценить, как были распределены частоты генотипов и аллелей в локальных популяциях лисиц на гигантской территории и как они менялись во времени – с XVII века по наши дни.

В отчете о меховых промыслах Российско-Американской компании за 1824 год написано «на острове Умнак добыто чернобурых – 40, сиводушек – 95, красных лисиц 51, на полуострове Нушагак - чернобурых – 1, сиводушек – 7, красных лисиц 121» и так далее по множеству локальных популяций. Поскольку по признаку окраски меха у лисиц есть полное соответствие между фенотипами и генотипами, мы можем оценить частоты генотипов в популяциях. Для этого разделим численность особей каждого генотипа на общий объем выборки (186 и 129 – соответственно). Получим в первой популяции следующие частоты генотипов ВВ = 0,215, Bb = 0,517, bb = 0,274; во второй ВВ = 0,008, Bb = 0,054, Bb = 0,938. Теперь оценим частоту аллеля В в этих популяциях. Каждая чернобурая лисица имела 2 аллеля В, сиводушка – 1 аллель В и 1 b, красные лисицы не имели ни одного аллеля В. Общее число обоих аллелей равно удвоенному числу особей в выборке. Следовательно частота аллеля В в первой популяции равна (2 х 40 + 95)/(2 х 186) = 0,470, а во второй – 0,035. Таким же способом можно подсчитать частоту аллеля b. Хотя можно сделать это и гораздо проще. Поскольку в популяции присутствуют только два аллеля гена В и b, то сумма их частот равна единице. Если частота аллеля В равна p, аллеля b равна q, то p + q =1. Отсюда находим частоту аллеля b: q =1- p. Это будет 0,530 в первой популяции и 0,965 во второй.

Сравнение разных популяций по частотам аллелей дает нам информацию о генетической гетерогенности видов в разнообразных условиях его обитания. Обратите внимание, что частота аллеля черной окраски в островных популяциях значительно выше, чем в континентальных. Причину этих различий между островными и континентальными популяциями мы обсудим позже, а пока проанализируем соотношение частот генотипов внутри популяций.

Это соотношение описывается уравнением Харди-Вейнберга. Оно было выведено в начале ХХ века математиком Г. Харди и врачом В.Вейнбрегом. Согласно этому уравнению, частоты генотипов в популяции определяются частотами аллелей. Если частота аллеля B равна р, а b равна q, частоты генотипов BB, Bb и bb равны p ², 2pq и q ²соответственно.

Уравнение Харди-Вейнберга и его биологический смысл. Уравнение Харди-Вейнберга базируется на законах Менделя. Каждая диплоидная особь в популяции возникает от слияния двух гаплоидных гамет. Следовательно частоты аллелей в популяции особей равны частотам аллелей в популяции гамет, от объединения которых эти особи возникли. Пусть доля сперматозоидов и яйцеклеток несущих аллель В равна р, а доля гамет несущих аллель b равна q. Если мы допускаем, что популяция достаточно многочисленна, и объединение гамет происходит случайно, то частоты возникших генотипов должны быть равны произведению частот гамет несущих аллели В и b. Вероятность оплодотворения яйцеклетки несущей аллель В сперматозоидом, несущим аллель В равна р х р = p ². Гомозиготы bb должны возникать с частотой q ². Слияние сперматозоида несущего В, с яйцеклеткой несущей b, происходит с частотой pq. С той же частотой происходит оплодотворение яйцеклетки, несущей В, сперматозоидом, несущим b. Тогда общая частота гетерозигот Bb равна 2pq. В общем виде мы можем записать зависимость частот генотипов от частот аллелей как

(p (B)+ q (b))x(p (B)+ q (b))= p ²(BB) + 2 pq (Bb) + q ²(bb).

Эта закономерность носит статистический характер, т.е. она выявляется в том случае, если численность популяции достаточно велика. Биологический смысл этого уравнения заключается в том, что распределение частот генотипов в популяции при условии случайного скрещивания между особями однозначно определяется частотами аллелей.

Популяция, в которой соотношение генотипов соответствует уравнению Харди-Вейнберга, называется равновесной. Равновесие частот генотипов в популяции поддерживается из поколения в поколение, если не нарушаются условия выполнения статистических закономерностей (вспомните § VI-4), то есть если скрещивания случайны, жизнеспособность особей с разными генотипами одинакова, а также не происходит изменения частот аллелей за счет мутаций, миграций или каких-либо других факторов.

Чтобы решить вопрос о том, находится ли та или иная популяция в состоянии равновесия, мы должны сравнить наблюдаемые соотношения генотипов с теми, которые должны были быть в этой популяции согласно уравнению Харди-Вейнберга. Проанализируем популяцию лисиц с острова Умнак, которую мы рассматривали выше. Подставим в уравнение Харди-Вейнберга значения частот аллелей, которые мы вычислили для реальной популяции. В этой популяции р = 0,470, а q =0,530. Тогда ожидаемое соотношение генотипов должно быть: ВВ = 0,221, Вb =0,498 и bb =0,281. Если мы умножим эти значения на количество животных в выборке, мы получим ожидаемые количества генотипов. Если популяция в лисиц острова Умнак находилась в 1824 году в состоянии равновесия, то в ней должно было быть 41 черная лисица, 93 сиводушки и 52 красных.

Сравнение достоверности различий между наблюдаемым и ожидаемым распределением частот проводят с использованием методов математической статистики. Но в данном случае и без статистики видно, что эти теоретически ожидаемые значения очень близки к тем, что наблюдались в действительности: 40 черных лисиц, 95 сиводушек и 51 красная. Отсюда мы можем заключить, эта популяция действительно находилась тогда в состоянии равновесия.

Что же может нарушить равновесие в популяции? Наиболее частой причиной нарушения равновесия является естественный отбор. Если генотипы отличаются друг от друга по выживаемости и плодовитости, то доля менее приспособленных генотипов оказывается меньше, чем должна быть по уравнению Харди-Вейнберга. Соответственно, из поколения в поколение падает и частота аллеля, который присутствует в таких генотипах. Однако если популяция достаточно велика, то в результате первого же цикла свободного скрещивания популяция вновь возвращается в состояние равновесия, хотя и при измененном соотношении частот генотипов.

Проведем мысленный эксперимент. Представим, что в популяции лисиц острова Умнак случились эпидемия, от которой погибли только красные лисицы. Численность популяции соответственно уменьшилась на 51 особь. В популяции осталось 40 черных и 95 сиводушек. Частота аллеля В р =(40 х 2 + 95)/(2 х 135)=0,648, а частота аллеля b q =1- p =0,352. Оставшиеся в живых лисицы случайно скрещиваются друг с другом. Черные лисицы образуют гаметы несущие только аллель В, а сиводушки образуют равное количество гамет несущих аллели В и b. Вероятность каждого конкретного сочетания гамет при условии случайного скрещивания равна произведению частот аллелей в популяции гамет. Поскольку частоты аллелей в родительской популяции изменились, изменятся и частоты генотипов в следующем поколении, но их соотношение вновь будет соответствовать уравнению Харди-Вейнберга: ВВ =0,420, Вb =0,456 и bb =0,124. После первого же цикла случайного скрещивания популяция вернулась в равновесное состояние. Она может оставаться в этом состоянии до тех пор, пока какой-либо из факторов не выведет ее из равновесия.

Известно несколько факторов, которые могут нарушать равновесие генотипов в популяции.

Мутационный процесс, низкая численность популяций, избирательность скрещиваний, миграции, естественный отбор.

Закон Харди — Вайнберга — это закон популяционной генетики — в популяции бесконечно большого размера, в которой не действует отбор, не идет мутационный процесс, отсутствует обмен особями с другими популяциями, не происходит дрейф генов, все скрещивания случайны — частоты генотипов по какому-либо гену (в случае если в популяции есть два аллеля этого гена) будут поддерживаться постоянными из поколения в поколение и соответствовать уравнению:

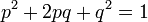
Date: 2015-09-02; view: 685; Нарушение авторских прав