
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Обратная матрица. Определение:Матрица называется обратной по отношению к квадратной матрице , если
|
|
Определение: Матрица 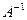 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 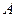 , если
, если
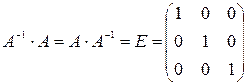 .
.
Обратная матрица существует только для квадратной матрицы, определитель которой не равен нулю. Такая матрица называется невырожденной.
Рассмотрим общий подход к нахождению обратной матрицы.
Рассмотрим на примере, как найти обратную матрицу 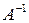 .
.
Пусть 
1)Найти определитель матрицы
 .
.
Так как 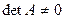 , то обратная матрица
, то обратная матрица 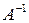 существует.
существует.
2) Сформировать матрицу из алгебраических дополнений каждого элемента матрицы.
|

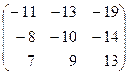
3) Транспонируем матрицу из алгебраических дополнений.
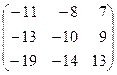 .
.
4) Обратная матрица 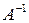 определяется формулой
определяется формулой
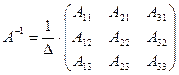 ,
,
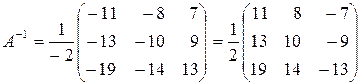 .
.
Укажем следующие свойства обратных матриц:
1. (A-1)-1 = A;
2. (AB)-1 = B-1A-1
3. (AT)-1 = (A-1)T.
Применение матриц к решению линейных уравнений.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальныхуравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Date: 2015-09-02; view: 359; Нарушение авторских прав
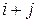 - четное число,
если
- четное число,
если