Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Закон Био-Савара-Лапласа и его практическое применение

Постоянные магниты и магнитные явления известны с глубокой древности. Компас применялся 3000 лет назад. Подробное описание постоянных магнитов их свойства, полюсы, взаимодействие было сделано Гильбертом еще в 1600 г. В 1820 г. опытами Эрстеда была экспериментально подтверждена связь магнитных явлений с электрическими. После опыта Эрстеда магнитные явления сводятся к электрическим (возник раздел физики – электромагнетизм), а магнитные силы по Энштейну есть релятивистская поправка к закону Кулона. Пока нет тока суммарный заряд электронов и ионов кристаллической решётки распределён равномерно и вместе нейтрален.

где 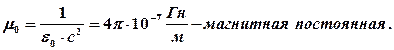За напр магн поля приним напр положит нормали в его равновесном положении. B=M_max/P_m=Fl/IS=μ₀H[Н/Ам=1Тесла]-инд магн поля. Инд магн поля равна макс вращ моменту действ на пробный контур единичн магн моментом. Инд магн поля явл-ся векторн велич.

Магнитная индукция величина векторная направление определяется по положительной нормали контура. Единицей магнитной индукции является тесла (Тл). Магнитное поле изображают с помощью линий магнитной индукции. Это линии, касательные к которым в каждой точке совпадают с направлением вектора 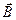. Они всегда замкнуты и охватывают проводники с током.

Этим они отличаются от линий напряженности электростатического поля, которые заканчиваются и начинаются на зарядах.

Закон Био ≈ Савара ≈ Лапласа и его применение к расчту магнитного поля

Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774≈1862) и Ф. Саваром (1791≈1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.

Закон Био ≈ Савара ≈ Лапласа для проводника с током I, элемент d l ═ которого создает в некоторой точке А (рис. 164) индукцию поля d B, записывается в виде

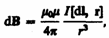════════════════════════════════════════════════════════ (110.1)

где d l ≈ вектор, по модулю равный длине d l элемента проводника и совпадающий по направлению с током, r ≈радиус-вектор, проведанный из элемента d l проводника в точку А поля, r ≈ модуль радиуса-вектора r. Направление d B перпендикулярно d l и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление враще╜ния головки винта дает направление d B, если поступательное движение винта соответ╜ствует направлению тока в элементе.

Модуль вектора d B определяется выражением

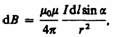═══════════════════════════════════════════════════════ (110.2)

где a ≈ угол между векторами d l и r.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

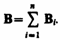════════════════════ ═══════════════════════════════════ (110.3)

Расч 232d35dc 077;т характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим╜метрию, то применение закона Био ≈ Савара ≈ Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.

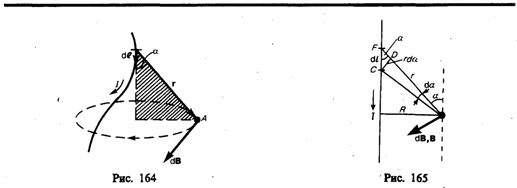
1. Магнитное поле прямого тока ≈ тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы d B от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа (╚к вам╩). Поэтому сложение векторов d B можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами d l и r), выразив через него все остальные величины. Из рис. 165 следует, что

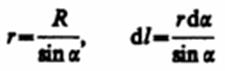
(радиус дуги CD вследствие малости d l равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индук╜ция, создаваемая одним элементом проводника, равна

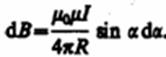══════════════════════════════════════════════════════════ (110.4)

Так как угол a ═для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),

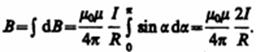
Следовательно, магнитная индукция поля прямого тока

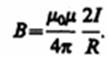═════════════════════════════════════════════════════════════ (110.5)

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления ≈ вдоль нормали от витка. Поэтому сложение век╜торов d B можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin a =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

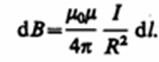
Тогда

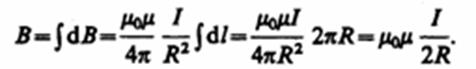
Следовательно, магнитная индукция поля в центре кругового проводника с током

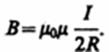
Date: 2015-08-24; view: 829; Нарушение авторских прав