Тригонометрическая и показательная формы

Если вещественную 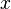и мнимую 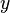части комплексного числа выразить через модуль и аргумент 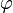(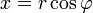, 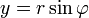), то всякое комплексное число , кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

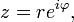
где 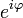— расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

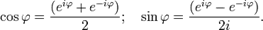
49.Свойства комплексных чисел:

Свойства комплексных чисел:

1) комплексные числа коммутативны по сложению и по умножению.

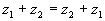
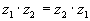
2) комплексные числа ассоциативны по сложению и по умножению.

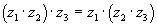
3) комплексные числа дистрибутивны.

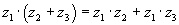
Для комплексных чисел операция деления определена как операция обратная операции умножения. Если 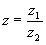, то z является решением уравнения 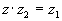. Решим это уравнение, домножив левую и правую часть на 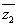и разделив обе части на квадрат модуля. Получим, что

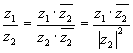
50. Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d) i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc) i (здесь как раз используется, что i ² = –1). Число 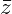= a – bi называется комплексно-сопряженным к z = a + bi. Равенство z · 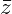= a ² + b ² позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:

.

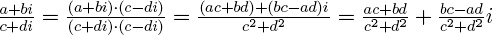(Например, .)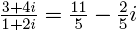

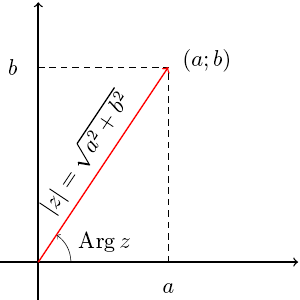У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна 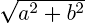. Эта величина называется модулем комплексного числа z = a + bi и обозначается | z |. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2 π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор.

51. Формула Муавра для комплексных чисел 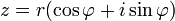утверждает, что

для любого

Date: 2015-08-24; view: 478; Нарушение авторских прав