Основные свойства гиперболы

Гипербола — это плоская кривая второго порядка, которая состоит из двух отдельных кривых, которые не пересекаются.
Формула гиперболы y = k/x, при условии, что k не равно 0. То есть вершины гиперболы стремятся к нолю, но никогда не пересекаются с ним.

Гипербола — это множество точек плоскости, модуль разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.

Свойства:

1. Оптическое свойство: свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
Иначе говоря, если F1 и F2 фокусы гиперболы, то касательная в любой точки X гиперболы является биссектрисой угла ∠F1XF2.

2. Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.

3. Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.

4. Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними.

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениям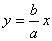и

и .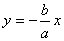

3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

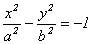, (11.3`)

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния r_i от точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

42. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F ₁ и F ₂ этой плоскости, называемых фокусами, есть величина постоянная.

Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.

| r₁ - r₂| = 2 a, откуда 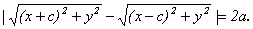Если обозначить b ² = c ² - a ², отсюда можно получить

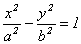- каноническое уравнение гиперболы. (11.3)

Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная 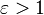называется эксцентриситетом гиперболы

Определение 11.6. Эксцентриситетом гиперболы называется величина е = с / а.

Эксцентриситет:

Определение 11.7. Директрисой D_i гиперболы, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.

43.Случай сопряжённой,вырожденной гиперболы (НЕ ПОЛНОСТЬЮ)

Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.

Если асимптоты гиперболы взаимно перпендикулярны, то гипербола называется равнобочной. Две гиперболы, имеющие общие асимптоты, но с переставленными поперечной и сопряженной осями, называются взаимно сопряженными.

44. Общее и каноническое уравнение параболы Для вывода уравнения параболы выберем декартову

систему координат так, чтобы ее началом была середина перпендикуляра FD, опущенного из фокуса на директрису, а координатные оси располагались параллельно и

перпендикулярно директрисе. Пусть длина отрезка FD равна р. Тогда из равенства r = d следует, что

поскольку

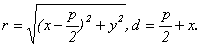Алгебраическими преобразованиями это уравнение можно привести к виду: y ² = 2 px,

называемому каноническим уравнением параболы. Величина р называется параметром параболы.

Date: 2015-08-24; view: 5622; Нарушение авторских прав