Методика викладання математики

1. Методика проведення позакласної роботи з математики. Питання методики поглибленого вивчення математики. Методика вивчення теми

2. Рівняння і нерівності в основній школі і методика їх вивчення.

3. Функції в курсі алгебри основної школи. Методика введення поняття функції. Підібрати задачі практичного змісту, які приводять до поняття функції у = kх, у = , у = kх + в.

4. Методика вивчення показникової, логарифмічної і степеневої функцій.

5. Методика розширення числових множин. Задачі на відсоткові розрахунки.

6. Методика вивчення тригонометричних функцій.

7. Методика вивчення елементів прикладної математики в шкільному курсі математики (математичне моделювання, наближені обчислення, елементи статистики, елементи комбінаторики, елементи теорії ймовірностей).

8. Вивчення алгебраїчних виразів і їх тотожних перетворень в шкільному курсі математики.

9. Методика вивчення тригонометричних рівнянь та нерівностей.

10. Методика вивчення і застосування похідної в шкільному курсі математики.

11. Методика вивчення показникових рівнянь і нерівностей.

12. Координати і вектори на площині і в просторі. Застосування до розв’язування задач.

13. Алгоритмічний підхід у навчанні математиці, його позитивні і негативні сторони.

14. Теореми, способи доведення теорем. Методика навчання учнів доведенню математичних тверджень.

1. Означення математичних понять. Види означень. Логічні помилки в означеннях понять.

16. Методика вивчення теми “Тіла обертання”.

17. Методика вивчення теми “Многогранники”.

18. Задачі в навчанні математики. Методика розв'язування математичних задач.

19. Методика введення первісної (поняття) та її застосування в шкільному курсі математики.

20. Об'єми і площі поверхонь геометричних тіл. Методика вивчення.

21. Діяльнісний підхід у навчанні математики. Зміст і роль загальних розумових дій і прийомів розумової діяльності (аналіз, синтез, порівняння, абстрагування. конкретизація, узагальнення, аналогія, індукція і дедукція).

22. Розв'язати нерівність: >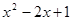

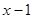
а) методом інтервалів,

б) методом систем,

в) графічним методом.

та розкрити методику розв’язування нерівностей.

23. Спростити вираз: 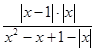різними способами та розкрити методику розв’язання завдань на спрощення виразів

24. Розв'язати нерівність: 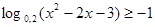та розкрити методику розв’язування логарифмічних нерівностей.

25. Довести різними способами, що медіани трикутника діляться у відношенні 2:1, починаючи від вершини.

26. Розв’язати ірраціональне рівняння: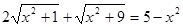

а) використовуючи властивість функцій;

б) безпосереднім піднесенням до степеня;

в)методом рівносильних перетворень

та розкрити методику розв’язування ірраціональних рівнянь.

27. Довести, що діагоналі ромба взаємно-перпендикулярні. Розв’язати дану задачу:

а) векторним методом,

б) традиційним методом.

28. Державний освітній стандарт з математики. Аналіз програм з математики для загальноосвітньої школи. Проблема досягнення обов’язкових результатів навчання.

29. Розв’язати рівняння 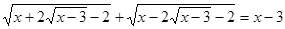різними методами та розкрити методику розв’язування рівнянь з модулями.

30. Геометричні величини (довжини, кутові величини, площі, об’єми), методика їх вивчення.

31. Розв’язати рівняння tg x - 2cos x = 1-tg x cos x різними способами та розкрити методику розв’язування тригонометричних рівнянь.

32. Методичні особливості вивчення теми “Коло і круг”.

33. Методика вивчення теми “Перпендикулярність прямих і площин в просторі”.

34. Геометричні побудови на площині і в просторі. Задачі на побудову.

35. Методика проведення перших уроків стереометрії.

36. Урок, вимоги до сучасного уроку математики в школі. Підготовка вчителя до уроку математики.

37. Методика вивчення теми “Паралельність прямих і площин в просторі”.

38. Методика вивчення теми “Подібність фігур”.

39. Методика проведення перших уроків планіметрії.

40. Методика вивчення теми “Чотирикутники”.

Рекомендована література:

1. Присяжнюк М.М. Конспекти лекцій з топології. – Рівне, 2006 (електронний варіант)

2. Яковець В.П., Боровик В.Н., Ваврикович Л.В. Аналітична геометрія – Суми: Університетська книга, 2004

3. Андрійчук В.І. Вступ до дискретної математики. Навчальний посібник. – К.: ЦНЛ, 2004. – 254с.

4. Перстюк М.О., Маринець В.В. Теорія рівнянь математичної фізики: Навч. посіб. для студ. фіз.-мат. спец. вищ.закл. освіти – 2 вид., перероб. й доповн. – К.: Либідь, 2001

5. Самарский А.А., Михайлов А.П. Математическое моделирование. – М.: Физматлит, 2001

6. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Изд-во МГУ, 2004

7. Михлин С.Г. Курс математической физики. – СПб: Лань, 2002

8. Бородін О.І., Потьомкін Л.В, Сліпенко А.К. Основні поняття сучасної алгебри. – К.: Вища школа, 1993. – 112с.

9. Скорняков Л.А. Элементы теории структур. – М.: Наука, 1982. – 158с.

10. Лидл Р., Нидеррайтер Г. Конечные поля. Т.1. – М.: Мир, 1988

11. Аминов Ю.А. Дифференциальная геометрия и топология кривых. – М., Наука, 1987

12. Рохлин В.А., Фукс Д.В, Начальный курс топологии. Геометрические главы. – М., Наука, 1977

13. Атанасян Л.С. Геометрия. – М.: Просвещение, ч.ІІ, 1986

14. Семенович О.Ф. Геометрія. Аксіоматичний метод. – К.: Вища школа, 1976

15. Погорелов А.В. Основания геометрии. – М.: Наука, 1968

Date: 2015-08-24; view: 615; Нарушение авторских прав