
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение систем линейных уравнений
|
|
Система линейных уравнений n -го порядка имеет вид:
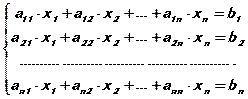
или в матричном виде:
AX=B,
где  ,
,  ,
, 
Корнями системы являются такие значения x1, x2,…xn, подстановка которых превращает уравнения системы в тождества.
Матричный метод. Зная матрицу A можно вычислить обратную матрицу A-1, затем умножить ее на систему: A-1×A×X=A-1×B.
Получится: X=A-1×B. Элементы вектора X и являются корнями системы линейных уравнений.
Чтобы решить систему в приложении Mathcad матричным методом надо записать коэффициенты системы − матрицу A. Далее задаётся вектор B и записывается формула для определения корней
X:=A-1×B
Корни вычисляются после набора выражения: X=
В приложении Excel также можно использовать матричный метод. Пусть имеется система линейных уравнений третьего порядка. Первоначально необходимо ввести элементы матрицы А, например, в ячейки А1:С3. Затем − вектор В, например, в ячейки Е1:Е3. Далее следует выделить диапазон ячеек для вычисления корней, например G1:G3 и в строке состояния набрать формулу:
=МУМНОЖ(МОБР(A1:C3);E1:E3)
После ее набора нажать не одну клавишу ввода, а вместе три клавиши: Shift-Ctrl-Enter. В ячейках G1:G3 появятся корни системы линейных уравнений.
Содержание заданий
1. Вычислить определенный интеграл для данных, приведенных в табл. 10.1 в приложении Mathcad.
2. Отделить корни уравнения f(x)=0, где f(x) берется из той же табл. 10.1.
3. Найти корни уравнения в приложении Excel с помощью команды Подбор параметра ив приложении Mathcad. Результаты сравнить между собой.
6. Решить произвольную систему линейных уравнений в приложениях Mathcad и Excel.
Таблица 10.1
| Номер вар. | Функция f(x) | Пределы интегрирования | Номер вар. | Функция f(x) | Пределы интегрирования |
| x2+4x-2 | a=1, b=2 | x3+3x-1 | a=4, b=8 | ||
| ln(x)+x-3 | a=3, b=4 | x3+x-4 | a=3, b=4 | ||
| x3+2x-1 | a=6, b=7 | ln(x)+x3 | a=3, b=7 | ||
| 2ln(x)-1/x | a=8, b=9 | ex-2x2-1 | a=2, b=9 | ||
| 2-x2+x | a=1, b=3 | 2x+ln(x)-7 | a=2, b=4 | ||
| 5x-1+x3 | a=2, b=5 | x3+2x-4 | a=1, b=5 | ||
| 1+ex+x | a=3, b=8 | 2+x+ln(x) | a=3, b=7 | ||
| x3+x-2 | a=6, b=9 | x3+x-3 | a=6, b=8 |
Date: 2015-08-24; view: 442; Нарушение авторских прав