Приближенное вычисление интегралов

Приближённое вычисление определённого интеграла основано на геометрическом смысле интеграла и сводится к приближённому вычислению площади, ограниченной подынтегральной функцией f(x), прямыми x=a=x₀, x=b=x_n и осью OX (рис. 10.1).

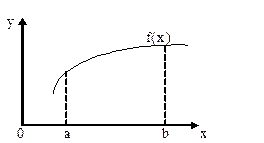Интервал [ a,b ] делится на n равных частей длиной .

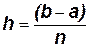Тогда значениям x_i=x_i-1+h, i=1,2...,n, соответствуют значения y_i=f(x_i).

Метод прямоугольников. В методе левых прямоугольников искомая площадь вычисляется как сумма площадей прямоугольников, основание которых равно h, а высота равна соответственно y₀ для первого прямоугольника, y₁ – для второго и т.д. вплоть до последнего с высотой y_n-1. Тогда

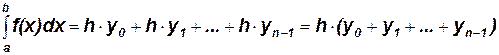
Для метода правых прямоугольников аналогично

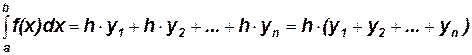
Метод трапеций. В методе трапеций определяется сумма площадей трапеций, основаниями которых являются ординаты y₀, y₁ и т.д., а высоты равны h.

Погрешность метода оценивается как 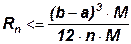, где М – максимальное значение второй производной f(x) на отрезке [a,b]. Используя это соотношение можно определить количество точек, на которое делится отрезок, исходя из заданной погрешности.

Чтобы вычислить определённый интеграл в приложении Mathcad нужно записать интеграл, подынтегральную функцию и пределы интегрирования. Например:

Для получения численного значения записывается выражение:

z=

Date: 2015-08-24; view: 429; Нарушение авторских прав